Вот скрипт друга

Array Names(1200):
Array CoordX(1200);
Array CoordY(1200);
set(R.260);
get N:
angle=2*math,pi/N;
for (i=1. i<=N, I++){get( Names(I))}
for (i=1. i<=N, I++){angle*i;
            CoordX( Names(I))=math.cos (angle)*R;
            CoordY( Names(I))=math.sin  (angle)*R;
 
while(end.data) { get (K);get(M);
  draw.line ((CoordX(K);CoordY(K)),(CoordX(M);CoordY(M))
};
for (i=1. i<=N, I++){ draw.circle ((CoordX(i);CoordY(i)).20));draw.Text(Names(i),(CoordX(i);CoordY(i));
;

Я тут ровным счётом ничего не понимаю.
Однако скрипт рисует!! Только у друга :)
Может быть, и у вас будет рисовать. Попробуйте-ка!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Мы нарисовали :)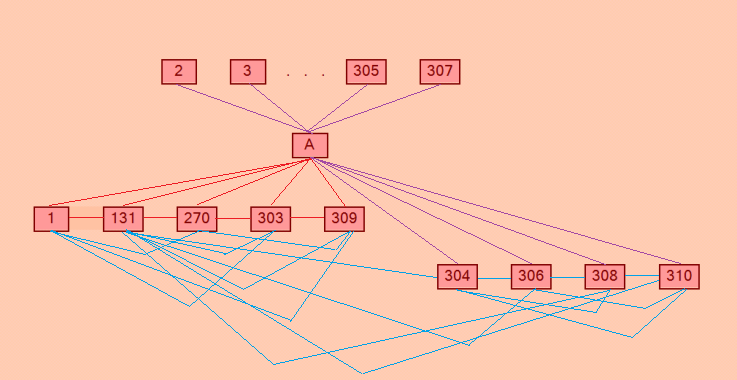



Не очень красиво, мы признаём :)

Здесь весьма интересная группа MODLS, состоящая аж из 6 взаимно ортогональных ДЛК:
A, 1, 131, 270, 303, 309
[Немножко неправильно я сделала: надо было всю группу MODLS из 6 ОДЛК рисовать красными линиями. Так и задумывалось, а потом забылось :) ]

Шесть взаимно ортогональных ОДЛК - это максимально возможное для порядка 9.

Покажите, пожалуйста, красивую иллюстрацию данной конфигурации.
Мы очень хотим её посмотреть! :)

PS. Показанная конфигурация содержит 172 КФ ОДЛК.
Никаких свойств у квадратов конфигурации утилита Harry White не обнаружила.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё одна конфигурация, порождаемая этим квадратиком

[DLK(360):81084]
0 2 8 7 6 3 5 4 1
4 1 0 6 3 7 2 8 5
1 7 2 8 0 4 3 5 6
8 5 4 3 7 6 1 0 2
5 6 1 0 4 8 7 2 3
6 8 7 2 1 5 4 3 0
2 3 5 4 8 0 6 1 7
3 0 6 1 5 2 8 7 4
7 4 3 5 2 1 0 6 8

Ну, тут круто: среди 360 ОДЛК имеется 162 ортогональные пары.
Таблица ортогональных пар

101:  96
102:  96
107:  96
108:  96
111:  96
114:  96
117:  96
118:  96
119:  96
121:  96
122:  96
124:  96
126:  96
128:  96
135:  96
136:  96
145:  24
148:  96
153:  96
155:  96
156:  96
157:  96
160:  96
163:  96
165:  96
167:  96 119
169:  96 126
171:  96 124
172:  96 122
173:  24 145
186:  96 121
190:  96 128
192:  96 136
193:  96 135
196:  96
197:  96
198:  96
199:  96
201:  96
203:  113
206:  96
208:  104
209:  96
212:  96
216:  96
217:  96
219:  96
220:  96
225:  96
226:  96
229:  96
230:  96
233:  24 145 173
241:  96 121 186
243:  96 122 172
244:  96 135 193
245:  96 136 192
248:  96 119 167
250:  96 126 169
251:  96 124 171
258:  96 128 190
260:  96
262:  96
264:  222
267:  96
268:  96
270:  214
273:  96
274:  96
275:  96
277:  96
280:  96
282:  96
284:  96
285:  96
287:  96
289:  96
290:  96
295:  96
296:  96 126 169 250
298:  96 122 172 243
300:  96 119 167 248
301:  96 121 186 241
304:  96 128 190 258
312:  96 124 171 251
320:  24 145 173 233
322:  96 136 192 245
324:  96 135 193 244
325:  96
327:  96
328:  96
331:  96
332:  293
334:  96
337:  279
338:  96
340:  96
342:  96
345:  162
346:  96
347:  96
349:  96
350:  96
352:  96
353:  96
357:  150
358:  96
359:  96

Таким образом, конфигурация первого уровня содержит 361 ОДЛК и 522 ортогональные пары.
Квадрат 96 очень крутой! Посчитайте, сколько у него ортогональных соквадратов.
Это сложно нарисовать вручную.
Оставляем для программы Gephi.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Вот полная система MOLS из 8 ЛК 9-го порядка, построенная в матпакете Maple



См. мою статью
http://www.natalimak1.narod.ru/grolk.htm
(рис. 7)

Назовём группу MODLS из 6 взаимно ортогональных ДЛК, которую видим на этой иллюстрации, группой MODLS №1.
В этой группе всего два уникальных ДЛК, вот их КФ

0 2 7 8 6 3 5 4 1
4 1 6 0 5 2 7 8 3
6 8 2 7 1 4 3 5 0
2 5 4 3 8 6 0 1 7
3 6 0 1 4 7 8 2 5
1 7 8 2 0 5 4 3 6
8 3 5 4 7 1 6 0 2
5 0 1 6 3 8 2 7 4
7 4 3 5 2 0 1 6 8

0 4 7 8 3 6 2 5 1
5 1 4 6 8 3 0 2 7
8 0 2 4 7 1 3 6 5
2 7 1 3 6 8 5 0 4
6 5 0 1 4 7 8 3 2
4 8 3 0 2 5 7 1 6
3 2 5 7 1 4 6 8 0
1 6 8 5 0 2 4 7 3
7 3 6 2 5 0 1 4 8

А теперь посмотрим на группу MODLS, состоящую из 6 взаимно ортогональных ДЛК, найденную мной (см. https://boinc.progger.info/odlk/forum_thread.php?id=169&postid=6542)

А
0 3 5 4 6 7 8 2 1
8 1 7 5 3 4 2 0 6
6 4 2 8 7 0 3 1 5
7 8 1 3 0 6 4 5 2
3 5 0 2 4 8 1 6 7
2 6 4 7 1 5 0 8 3
1 7 8 0 5 2 6 3 4
4 2 6 1 8 3 5 7 0
5 0 3 6 2 1 7 4 8

1
0 3 2 5 6 4 7 1 8
8 2 1 7 5 0 6 3 4
5 6 7 0 8 1 2 4 3
3 4 0 1 2 7 8 6 5
7 5 6 8 4 3 1 0 2
4 1 3 6 7 8 5 2 0
6 7 5 4 0 2 3 8 1
2 0 8 3 1 6 4 5 7
1 8 4 2 3 5 0 7 6

131
3 0 4 6 7 1 2 8 5
8 7 6 1 5 4 3 2 0
1 2 5 0 3 7 6 4 8
7 6 8 2 1 3 0 5 4
4 3 0 7 8 5 1 6 2
2 5 1 4 0 6 8 3 7
6 8 7 5 2 0 4 1 3
5 1 2 3 4 8 7 0 6
0 4 3 8 6 2 5 7 1

270
2 7 0 6 5 1 3 8 4
6 3 7 5 2 4 0 1 8
4 8 1 0 3 6 5 7 2
0 2 5 4 8 7 1 6 3
8 1 4 7 0 5 2 3 6
5 0 3 2 6 8 7 4 1
1 4 8 3 7 2 6 0 5
7 6 2 8 1 3 4 5 0
3 5 6 1 4 0 8 2 7

303
1 7 8 4 0 3 5 6 2
7 4 5 1 3 6 2 0 8
5 3 7 0 8 2 6 1 4
6 2 3 8 7 4 1 5 0
2 6 4 3 5 8 0 7 1
4 1 2 7 6 0 8 3 5
8 0 1 6 2 5 3 4 7
0 8 6 5 4 1 7 2 3
3 5 0 2 1 7 4 8 6

309
3 4 5 2 1 6 7 8 0
5 8 0 4 7 1 6 2 3
8 5 1 0 2 4 3 7 6
7 1 2 6 0 5 8 3 4
2 0 7 3 4 8 5 6 1
0 2 3 8 6 7 1 4 5
4 3 6 5 8 2 0 1 7
6 7 4 1 3 0 2 5 8
1 6 8 7 5 3 4 0 2

Эту группу назовём группой MODLS №2.
Это новая группа не изоморфная группе №1.
В этой группе тоже два уникальных ДЛК, показываю их КФ

0 2 7 6 8 3 5 4 1
3 1 6 5 0 8 7 2 4
6 8 2 1 7 4 3 5 0
4 7 8 3 2 6 1 0 5
1 5 3 0 4 7 2 8 6
2 6 0 8 1 5 4 3 7
8 4 5 7 3 0 6 1 2
5 0 1 4 6 2 8 7 3
7 3 4 2 5 1 0 6 8

0 3 5 4 6 7 8 2 1
8 1 7 5 3 4 2 0 6
6 4 2 8 7 0 3 1 5
7 8 1 3 0 6 4 5 2
3 5 0 2 4 8 1 6 7
2 6 4 7 1 5 0 8 3
1 7 8 0 5 2 6 3 4
4 2 6 1 8 3 5 7 0
5 0 3 6 2 1 7 4 8

В группе №1 ДЛК ассоциативные, в группе №2 – не ассоциативные.

Для проверки ввела все ДЛК группы №2 в программу Harry White GetOrthogonal, конечно, без номеров ДЛК; номера будут (по умолчанию) 1, 2, 3, 4, 5, 6 соответственно расположению квадратов.
Программа выдала следующую таблицу ортогональных пар

2:  1
3:  1 2
4:  1 2 3
5:  1 2 3 4
6:  1 2 3 4 5

Всё верно, имеем 15 ортогональных пар от 6 взаимно ортогональных ДЛК.

Итак, мы имеем две различные группы MODLS 9-го порядка. Это максимально возможные группы MODLS данного порядка (из 6 ДЛК).
В теме BOINC project Rake Search я приводила ссылку на статью, в которой опубликовано несколько групп MODLS 9-го порядка.
По виду ДЛК в этих группах разные, но вот насчёт изоморфности пока не знаю, это я не проверяла.
Можно проверить на досуге.
Интересен вопрос: сколько всего существенно различных групп MODLS 9-го порядка, состоящих из 6 взаимно ортогональных ДЛК?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Статья, конечно, называется не "Handbook of Combinatorial Design", а "Mutually Orthogonal Latin Squares (MOLS)", авторы R. Julian R. Abel, Charles J. Colbourn, Jeffrey H. Dinitz.
В статье приведено много комплектов MOLS 9-го порядка. Надо понять, что это за комплекты, а для этого хорошо знать английский язык.

Я выложила статью на Яндекс.Диск
https://yadi.sk/i/x1w4tkQx3MsvHw

Может, кому-то интересно разобраться с этими комплектами (о них в главе 3.5 "Complete Sets of Order 9", стр. 171)

Статья даже выложена на Яндекс.Диск.
Исследуйте на здоровье.

PS. Сейчас просмотрела статью прямо на Яндекс.Диске; в статье приведено 19 групп, это полные группы MOLS 9-го порядка, но в них есть и ДЛК. Может быть, не во всех есть, надо проверить.
Там формат очень плохой, ничего не разберёшь.
Впрочем, кажется, я это всё исследовала в теме BOINC project Rake Search, проверила все 19 групп.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Покажу конфигурацию для ДЛК 11-го порядка

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

Это ДЛК из полной системы MOLS.
Программой Белышева ortogon_u найдено 26914 ортогональных ДЛК к этому ДЛК.
Среди этих 26914 ОДЛК утилита Harry White нашла 186 ортогональных пар

Order? 11

Enter the name of the squares file: inp
..output file inpPairs_1.txt
..output file inpPairNos_1.txt
squares 26914 orthogonal pairs 186

elapsed time 0:02:41

Поиск быстрый - около 3 минут.
Таблица ортогональных пар, выданная утилитой

6423:  1800
11107:  1800 6423
11489:  1800 6423 11107
18550:  453 454 457 463 464 465 466 467 470 471
 492 493 499 517 531 1690 1749 1800 4891 4901
 4906 4908 4909 4917 4920 4921 4953 4954 4957 4958
 4959 4963 4964 6362 6419 6423 9131 9132 9138 9156
 9157 9158 9163 9177 9179 9183 9189 9207 9208 9210
 9211 11060 11102 11107 11180 11181 11186 11188 11190 11191
 11202 11203 11220 11234 11235 11250 11259 11260 11261 11477
 11487 11489 11536 11558 11581 11724 11725 11727 11728 11731
 11732 11735 11739 11749 11782 11795 11796 11798 11805 11806
 12069 12079 12080 12081 12085 12086 12099 12102 12107 12108
 12116 12117 12136 12137 12144 13240 13241 13242 13246 13247
 13258 13263 13264 13271 13276 13277 13281 13282 13283 13317
 14627 14628 14651 14653 14654 14656 14659 14660 14679 14680
 14691 14693 14695 14702 14704
19547:  18550
19561:  1800 6423 11107 11489 18550
19682:  18550
20696:  18550
20722:  18550
20723:  18550
20740:  18550
20741:  18550
20742:  18550
20750:  18550
20751:  18550
20754:  18550
20759:  18550
20761:  18550
20768:  18550
20773:  18550
20774:  18550
20777:  18550
24784:  1800 6423 11107 11489 18550 19561
24786:  18550
24795:  18550
26378:  18550
26383:  18550
26390:  18550
26393:  18550
26394:  18550
26396:  18550
26398:  18550
26401:  18550
26403:  18550
26407:  18550
26408:  18550
26426:  18550
26427:  18550
26428:  18550
26448:  18550

Очень интересная конфигурация. Это, конечно, только первый уровень.
Конфигурация содержит 26915 ОДЛК (включая исходный ДЛК) и 27100 ортогональных пар.
Конечно, полностью нарисовать конфигурацию вручную невозможно; попробую нарисовать группу MODLS из 8 взаимно ортогональных ДЛК.
Это максимально возможная группа MODLS для ДЛК 11 порядка.
Интересный тут квадратик 18550, он входит в группу MODLS и имеет много других ортогональных диагональных соквадратов.
Исходный ДЛК обозначу А.
Группа MODLS:
A, 1800, 6423, 11107, 11489, 18550, 19561, 24784

Естественно, что квадрат А дал группу MODLS из 8 взаимно ортогональных ДЛК: он из полной системы MOLS.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Я скачала программу Gephi.
Товарищи! Господа!
Расскажите, пожалуйста, как тут надо рисовать.
Ну, вот методом тыка получилась такая картинка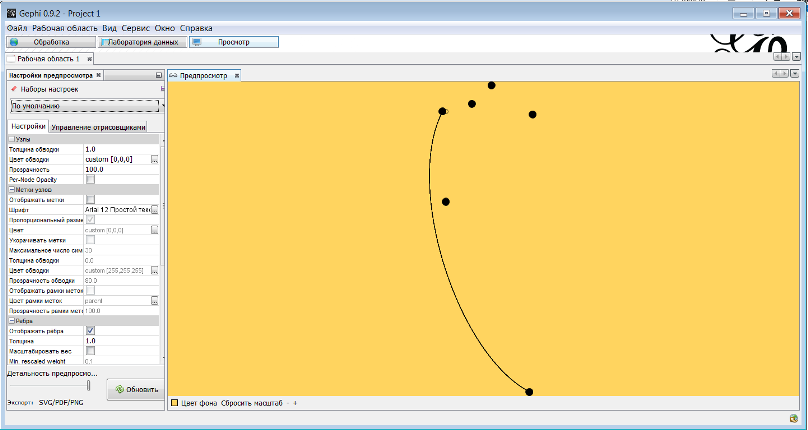



Узлы добавила, рёбра - не знаю как добавлять.

Уже близка к цели.
Если вы мне чуть-чуть подскажете, дело пойдёт :)
Я хотя бы на правильном пути?
Надо же ещё знать, как ввести данные в программу из файла.
Не вручную же все узлы и рёбра вводить.

Какой формат данных должен быть во входном файле?
Какой должен быть сам файл - txt?
Там я вижу в левом верхнем углу написано Файл.
Это тот самый файл, который содержит данные? Или нет?

А инструкция здесь имеется? Может, надо посмотреть "Справка"?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот ещё методом тыка нарисовала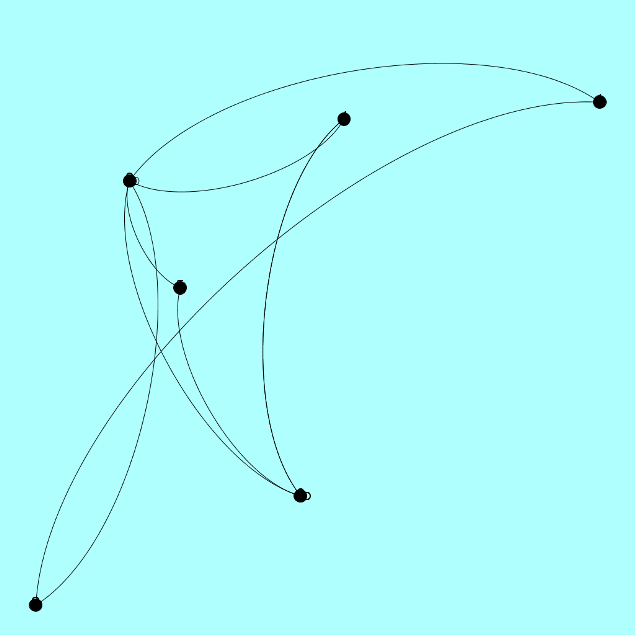



Уже записала картинку в файл.

Но не получилось! Мне надо все узлы друг с другом соединить. Я задаю все рёбра.
А она не соединяет все узлы :(

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

У-р-р-р-а-а-а!
Черепашка ликует :)
С утречка на свежую голову всё получилось.
Встречайте - MODLS 9-го порядка (6 взаимно ортогональных ДЛК)



Нарисовано программой Gephi.
Ой, красиво как!

Осталась самая малость - узнать, как вводить данные из файла.
А господа молчат :) Они знают, но не хотят мне сказать, да? :)

Покажу живые квадратики (которые скрываются за узлами на иллюстрации)

0 3 5 4 6 7 8 2 1
8 1 7 5 3 4 2 0 6
6 4 2 8 7 0 3 1 5
7 8 1 3 0 6 4 5 2
3 5 0 2 4 8 1 6 7
2 6 4 7 1 5 0 8 3
1 7 8 0 5 2 6 3 4
4 2 6 1 8 3 5 7 0
5 0 3 6 2 1 7 4 8

0 3 2 5 6 4 7 1 8
8 2 1 7 5 0 6 3 4
5 6 7 0 8 1 2 4 3
3 4 0 1 2 7 8 6 5
7 5 6 8 4 3 1 0 2
4 1 3 6 7 8 5 2 0
6 7 5 4 0 2 3 8 1
2 0 8 3 1 6 4 5 7
1 8 4 2 3 5 0 7 6

3 0 4 6 7 1 2 8 5
8 7 6 1 5 4 3 2 0
1 2 5 0 3 7 6 4 8
7 6 8 2 1 3 0 5 4
4 3 0 7 8 5 1 6 2
2 5 1 4 0 6 8 3 7
6 8 7 5 2 0 4 1 3
5 1 2 3 4 8 7 0 6
0 4 3 8 6 2 5 7 1

2 7 0 6 5 1 3 8 4
6 3 7 5 2 4 0 1 8
4 8 1 0 3 6 5 7 2
0 2 5 4 8 7 1 6 3
8 1 4 7 0 5 2 3 6
5 0 3 2 6 8 7 4 1
1 4 8 3 7 2 6 0 5
7 6 2 8 1 3 4 5 0
3 5 6 1 4 0 8 2 7

1 7 8 4 0 3 5 6 2
7 4 5 1 3 6 2 0 8
5 3 7 0 8 2 6 1 4
6 2 3 8 7 4 1 5 0
2 6 4 3 5 8 0 7 1
4 1 2 7 6 0 8 3 5
8 0 1 6 2 5 3 4 7
0 8 6 5 4 1 7 2 3
3 5 0 2 1 7 4 8 6

3 4 5 2 1 6 7 8 0
5 8 0 4 7 1 6 2 3
8 5 1 0 2 4 3 7 6
7 1 2 6 0 5 8 3 4
2 0 7 3 4 8 5 6 1
0 2 3 8 6 7 1 4 5
4 3 6 5 8 2 0 1 7
6 7 4 1 3 0 2 5 8
1 6 8 7 5 3 4 0 2

Эта группа MODLS 9-го порядка найдена мной, я её назвала "группа №2".
Группа №1 - это давно известная группа из полной системы MOLS (см. выше иллюстрацию полной системы MOLS).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Встречайте - MODLS 11-го порядка (8 взаимно ортогональных ДЛК)



Нарисовано программой Gephi.

Пока ввожу данные вручную.

PS. Вчера я собиралась эту группу MODLS 11-го порядка вручную рисовать.
Ну, так красиво не получилось бы :)

Показываю живые квадратики к этой иллюстрации - это 8 ДЛК из полной системы MOLS 11-го порядка

0 1 2 3 4 5 6 7 8 9 10
2 3 4 5 6 7 8 9 10 0  1
4 5 6 7 8 9 10 0  1 2 3
6 7 8 9 10 0  1 2 3 4 5
8 9 10 0  1 2 3 4 5 6 7
10 0  1 2 3 4 5 6 7 8 9
1 2 3 4 5 6 7 8 9 10 0
3 4 5 6 7 8 9 10 0 1 2
5 6 7 8 9 10 0 1 2 3 4
7 8 9 10 0 1 2 3 4 5 6
9 10 0 1 2 3 4 5 6 7 8

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

0 1 2 3 4 5 6 7 8 9 10
4 5 6 7 8 9 10 0 1 2 3
8 9 10 0 1 2 3 4 5 6 7
1 2 3 4 5 6 7 8 9 10 0
5 6 7 8 9 10 0 1 2 3 4
9 10 0 1 2 3 4 5 6 7 8
2 3 4 5 6 7 8 9 10 0 1
6 7 8 9 10 0 1 2 3 4 5
10 0 1 2 3 4 5 6 7 8 9
3 4 5 6 7 8 9 10 0 1 2
7 8 9 10 0 1 2 3 4 5 6

0 1 2 3 4 5 6 7 8 9 10
5 6 7 8 9 10 0 1 2 3 4
10 0 1 2 3 4 5 6 7 8 9
4 5 6 7 8 9 10 0 1 2 3
9 10 0 1 2 3 4 5 6 7 8
3 4 5 6 7 8 9 10 0 1 2
8 9 10 0 1 2 3 4 5 6 7
2 3 4 5 6 7 8 9 10 0 1
7 8 9 10 0 1 2 3 4 5 6
1 2 3 4 5 6 7 8 9 10 0
6 7 8 9 10 0 1 2 3 4 5

0 1 2 3 4 5 6 7 8 9 10
6 7 8 9 10 0 1 2 3 4 5
1 2 3 4 5 6 7 8 9 10 0
7 8 9 10 0 1 2 3 4 5 6
2 3 4 5 6 7 8 9 10 0 1
8 9 10 0 1 2 3 4 5 6 7
3 4 5 6 7 8 9 10 0 1 2
9 10 0 1 2 3 4 5 6 7 8
4 5 6 7 8 9 10 0 1 2 3
10 0 1 2 3 4 5 6 7 8 9
5 6 7 8 9 10 0 1 2 3 4

0 1 2 3 4 5 6 7 8 9 10
7 8 9 10 0 1 2 3 4 5 6
3 4 5 6 7 8 9 10 0 1 2
10 0 1 2 3 4 5 6 7 8 9
6 7 8 9 10 0 1 2 3 4 5
2 3 4 5 6 7 8 9 10 0 1
9 10 0 1 2 3 4 5 6 7 8
5 6 7 8 9 10 0 1 2 3 4
1 2 3 4 5 6 7 8 9 10 0
8 9 10 0 1 2 3 4 5 6 7
4 5 6 7 8 9 10 0 1 2 3

0 1 2 3 4 5 6 7 8 9 10
8 9 10 0 1 2 3 4 5 6 7
5 6 7 8 9 10 0 1 2 3 4
2 3 4 5 6 7 8 9 10 0 1
10 0 1 2 3 4 5 6 7 8 9
7 8 9 10 0 1 2 3 4 5 6
4 5 6 7 8 9 10 0 1 2 3
1 2 3 4 5 6 7 8 9 10 0
9 10 0 1 2 3 4 5 6 7 8
6 7 8 9 10 0 1 2 3 4 5
3 4 5 6 7 8 9 10 0 1 2

0 1 2 3 4 5 6 7 8 9 10
9 10 0 1 2 3 4 5 6 7 8
7 8 9 10 0 1 2 3 4 5 6
5 6 7 8 9 10 0 1 2 3 4
3 4 5 6 7 8 9 10 0 1 2
1 2 3 4 5 6 7 8 9 10 0
10 0 1 2 3 4 5 6 7 8 9
8 9 10 0 1 2 3 4 5 6 7
6 7 8 9 10 0 1 2 3 4 5
4 5 6 7 8 9 10 0 1 2 3
2 3 4 5 6 7 8 9 10 0 1

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Сейчас попробую нарисовать конфигурацию из стартового поста.

О-о-о! Какой вкусный рогалик :)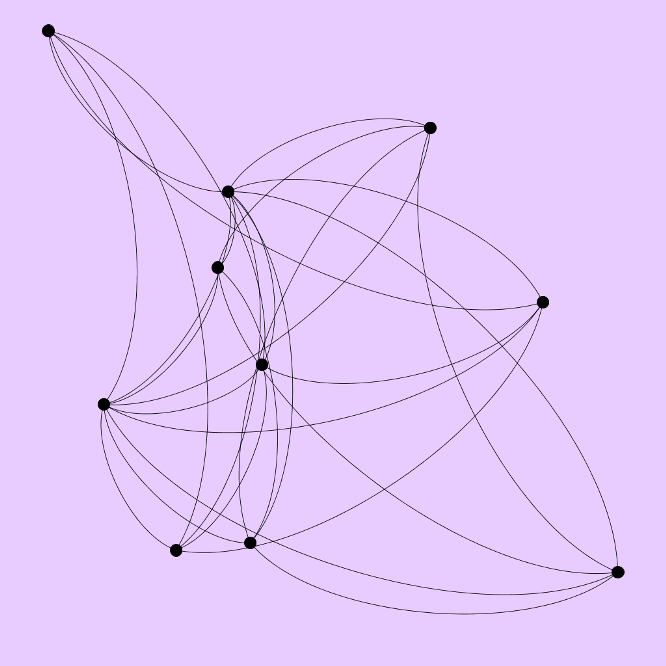



Живые квадраты для этой иллюстрации показаны в начале темы
https://boinc.progger.info/odlk/forum_thread.php?id=169&postid=6473

Сравните с иллюстрацией, которую нарисовал друг с помощью своего скрипта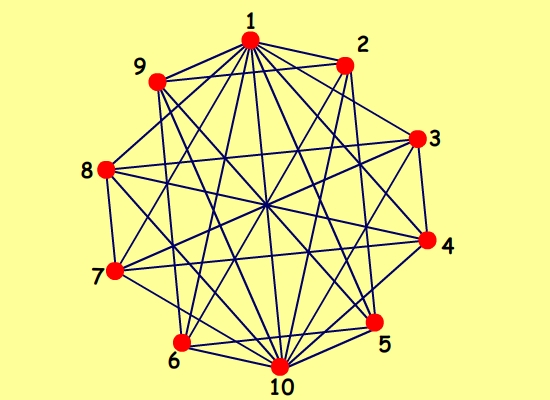

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Никак не найду управление цветом узлов и рёбер.
Настройки есть, но ничего не могу понять.

Тэк-с, совсем близка к осуществлению розовой мечты :)
Как, ну как мне импортировать в программу эту таблицу ортогональных пар
https://boinc.progger.info/odlk/forum_thread.php?id=169&postid=6469 ???

Я понимаю, что её надо записать в файл. Какой формат записи в файл? Какой тип файла?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё и так рисует программа Gephi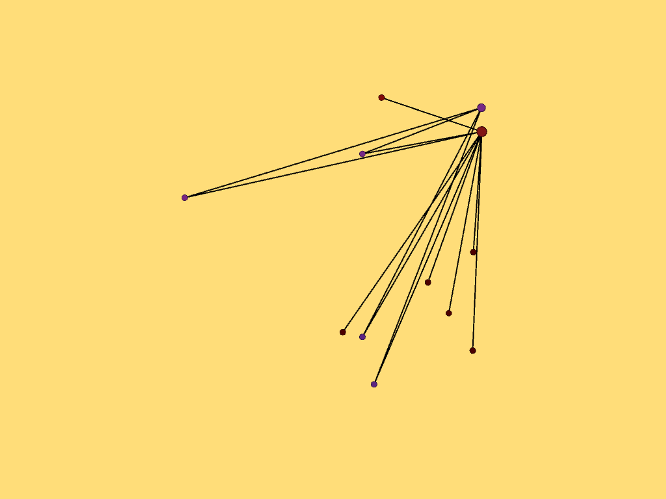



Это моя рекордная конфигурация для ОДЛК 10-го порядка (десяточка).
Тут мало узлов и рёбер, вручную легко ввести.

Сравните с иллюстрацией для этой же конфигурации, нарисованной Demis вручную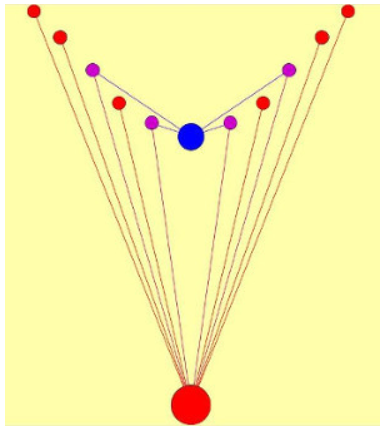



У Demis красивее.
Наверное, и в программе Gephi можно настроить, чтобы симметрия была.
Но я пока не знаю - как.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Сейчас нарисую в Gephi эту конфигурацию

5:  1 4
6:  1 2 3 4
7:  6
8:  5 6
9:  6
10:  5 6

Иллюстрация, нарисованная вручную, здесь
https://boinc.progger.info/odlk/forum_thread.php?id=169&postid=6535

Готово!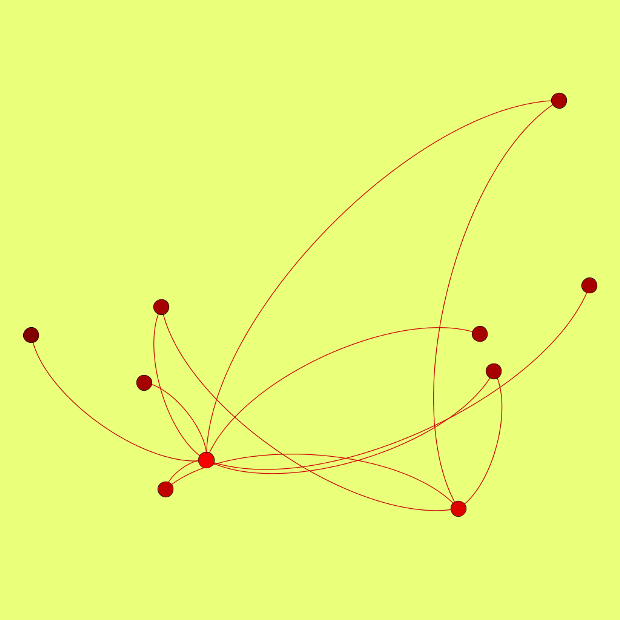



Сравните с иллюстрацией для этой же конфигурации; мы с черепашкой вручную рисовали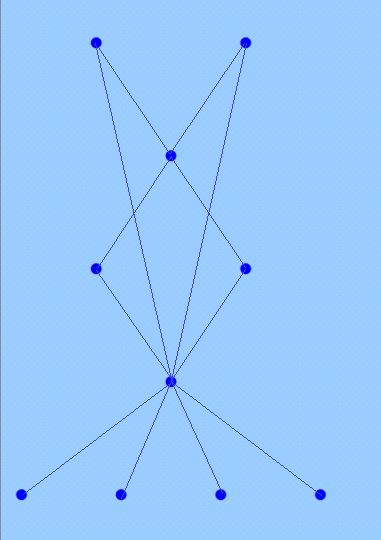

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Уф!
Хорошо порисовали :)
А подсказки всё нет :(
Куда же мне ещё обратиться за подсказкой?
Помощь друга не работает, помощь зала не работает.
Может, в Спортлото написать? :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Немножко изменила последнюю иллюстрацию



Там можно перетаскивать узлы, что я и сделала.
Вроде стало лучше.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Там есть функционал Импортировать из CSV.
Это, кажется, то самое, что мне нужно.
Но что такое CSV?
Как его создать, чтобы потом импортировать в программу?

PS. Я создала текстовый файл, записала в него рёбра графа

0 - 4
0 - 5
1 - 5
2 - 5
3 - 4
3 - 5
4 - 7
4 - 9
5 - 6
5 - 7
5 - 8
5 - 9

и попробовала этот файл импортировать.
Нет, не такой файл. Написано, что такой тип файла не поддерживается.
Значит, файл должен быть другого типа.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Нашла документацию!!
Вот

Gephi поддерживает файлы CSV, которые просто представляют отношения. Формат CSV можно получить из любых строковых данных, баз данных или экспорта в Excel. Каждая строка должна содержать как минимум два элемента, разделенных разделителем (запятая, точка с запятой, вертикальная черта или пробел). Значения можно заключить в одинарные или двойные кавычки. По умолчанию графики, импортированные из CSV, являются ориентированными, но пользователь может выбрать неориентированные в диалоговом окне отчета импорта.

Так, ребята, ещё немного, ещё чуть-чуть :)
Если гора не идёт к Магомету, Магомет идёт к горе.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Есть!
Импортирование получилось!
Для маленькой конфигурации.
Сейчас попробую большую конфигурацию.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Импортировала эту конфигурацию

206;29
318;60
400;29;206
424;60;318
438;13;14;17;18;19;22;24;29;31;38
438;43;45;47;48;50;51;53;56;57;58
438;59;60;61;63;64;65;179;180;190;194
438;200;201;202;203;204;206;207;208;209;212
438;215;219;227;245;250;304;308;314;318;325
438;328;347;380;382;392;394;396;397;398;400
438;402;403;404;414;416;422;423;424;425;426
438;427;428;430;431;433;434;435;436
462;438
466;438
471;438
473;438
474;438
476;438
477;29;206;400;438
478;438
483;438
488;438
490;438
492;438
494;438
500;438
502;438
503;438
504;438
505;60;318;424;438
506;438
507;438
509;438
510;438
511;438
513;438
514;438
516;438

Кстати, для друга: преобразовывается в Ворде элементарно!
Всё получилось, граф загрузился и изобразился



Остался последний шаг - не получилось изображение с дуговыми (кривыми) рёбрами графа.
Ну да и шут с ним.
Уже видно, что розовая мечта осуществилась и... увы - ничего хорошего.
Ну что тут можно понять? Никакой наглядности нет.
Хороши иллюстрации, на которых всё чётко видно: узлы и рёбра.

В общем, я разочаровалась.
Но зато теперь знаю, как рисовать программой Gephi.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg