Программа Gephi. Рисуем!
Message boards :
Science :
Программа Gephi. Рисуем!
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я писала об этой программе тут https://boinc.progger.info/odlk/forum_thread.php?id=44&postid=6303 Процитирую сообщение с форума Math Help Planet 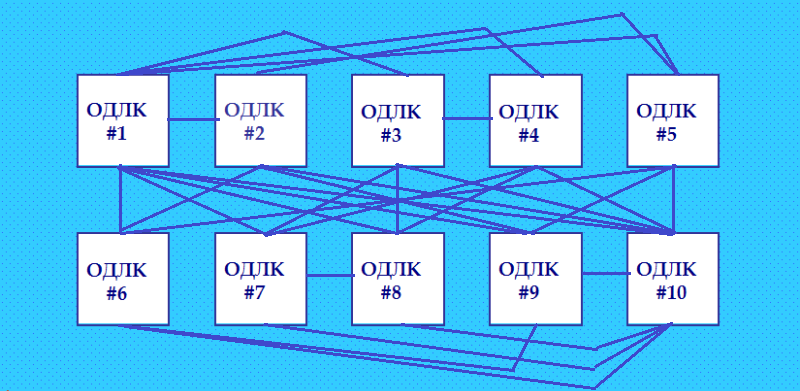 ОДЛК изображены квадратиками, на которых написаны номера ОДЛК. Приведу таблицу ортогональных пар в этой группе ОДЛК, как её выдаёт утилита Harry White (таблица ортогональных пар составляется на основе введённых в программу ОДЛК) 2: 1 3: 1 4: 1 3 5: 1 2 6: 1 2 5 7: 1 3 4 8: 1 3 4 7 9: 1 2 5 6 10: 1 2 3 4 5 6 7 8 9 Иллюстрацию я вручную рисовала. А эту иллюстрацию нарисовал друг 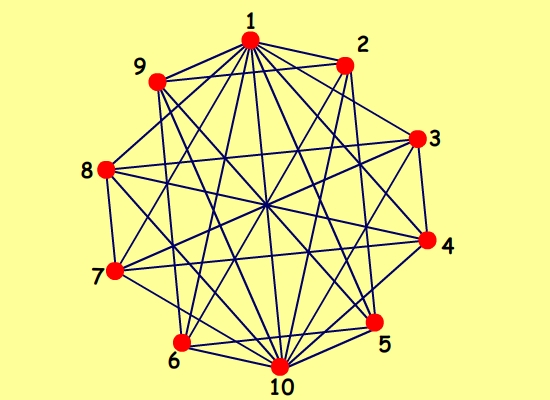 Да, у него, конечно, красивее получилось, симметрия. Интересно, как нарисовала бы программа Gephi эту конфигурацию ОДЛК. Господа! Приглашаю вас порисовать. Ну, с этой простенькой конфигурацией уже всё понятно. Далее покажу конфигурацию посложнее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я пока не отважилась скачать программу и посмотреть, что там и как. По-английски читать не умею :( А заинтересовать народ ну никак не получается. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Теперь исследуем конфигурацию, порождаемую совершенным ДЛК 9-го порядка, вот он какой красивый  Как утверждает программа Белышева ortogon_u, этот ДЛК имеет 308 ОДЛК Проверка ДЛК9 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 333 Соквадратов: 308 Время в сек: 5 И это только первый уровень, наверняка от этих 308 ОДЛК потянутся ветви. Но это я ещё не проверяла. Интересно посмотреть хотя бы на первый уровень. Утилита Harry White находит в этой группе из 308 ОДЛК 116 ортогональных пар. Таким образом, конфигурация содержит 309 ОДЛК (включая сам совершенный ДЛК) и 424 ортогональные пары. Хорошая конфигурация! Вот бы нарисовать иллюстрацию. Прям розовая мечта :) Далее покажу таблицу ортогональных пар. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот таблица ортогональных пар для группы ОДЛК, порождаемой совершенным ДЛК, как её выдаёт утилита Harry White GetOrthogonal 2: 1 3: 1 4: 1 5: 1 6: 1 7: 1 8: 1 9: 1 10: 1 11: 1 12: 1 13: 1 14: 1 15: 1 16: 1 17: 1 18: 1 19: 1 20: 1 21: 1 22: 1 23: 1 24: 1 25: 1 26: 1 27: 1 28: 1 29: 1 30: 1 31: 1 32: 1 33: 1 34: 1 35: 1 36: 1 37: 1 38: 1 39: 1 40: 1 41: 1 42: 1 43: 1 44: 1 45: 1 46: 1 47: 1 48: 1 49: 1 50: 1 51: 1 52: 1 53: 1 54: 1 55: 1 56: 1 57: 1 58: 1 59: 1 60: 1 61: 1 62: 1 63: 1 64: 1 65: 1 66: 1 67: 1 68: 1 69: 1 70: 1 71: 1 72: 1 73: 1 9 74: 1 75: 1 76: 1 77: 1 78: 1 79: 1 80: 1 81: 1 82: 1 83: 1 84: 1 85: 1 86: 1 87: 1 88: 1 89: 1 90: 1 91: 1 92: 1 93: 1 94: 1 95: 1 96: 1 97: 1 98: 1 99: 1 100: 1 101: 1 102: 1 48 103: 1 104: 1 105: 1 106: 1 107: 1 108: 1 109: 1 110: 1 111: 1 112: 1 113: 1 114: 1 115: 1 116: 1 48 102 117: 1 118: 1 119: 1 120: 1 121: 1 122: 1 123: 1 124: 1 125: 1 126: 1 127: 1 128: 1 129: 1 130: 1 131: 1 132: 1 133: 1 134: 1 135: 1 136: 1 137: 1 138: 1 139: 1 140: 1 141: 1 142: 1 143: 1 144: 1 9 73 145: 1 146: 1 147: 1 148: 1 149: 1 150: 1 151: 1 152: 1 153: 1 154: 1 155: 1 156: 1 157: 1 158: 1 159: 1 160: 1 161: 1 162: 1 163: 1 164: 1 165: 1 166: 1 167: 1 168: 1 169: 1 170: 1 171: 1 172: 1 173: 1 174: 1 175: 1 176: 1 177: 1 178: 1 179: 1 180: 1 181: 1 182: 1 183: 1 184: 1 185: 1 186: 1 187: 1 188: 1 189: 1 190: 1 191: 1 192: 1 193: 1 194: 1 195: 1 196: 1 197: 1 198: 1 199: 1 200: 1 201: 1 202: 1 203: 1 204: 1 205: 1 206: 1 207: 1 208: 1 209: 1 210: 1 211: 1 212: 1 213: 1 2 3 6 7 8 9 11 13 14 15 16 23 24 39 40 41 42 44 45 46 47 48 49 50 51 52 69 70 71 72 73 74 75 77 79 84 85 89 90 92 93 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 112 113 114 115 116 117 118 119 120 137 138 139 140 142 143 144 145 147 149 150 153 154 214: 1 215: 1 216: 1 217: 1 218: 1 219: 1 220: 1 221: 1 222: 1 223: 1 224: 1 225: 1 226: 1 227: 1 228: 1 229: 1 230: 1 231: 1 232: 1 233: 1 234: 1 235: 1 236: 1 237: 1 238: 1 239: 1 240: 1 241: 1 242: 1 243: 1 244: 1 245: 1 246: 1 247: 1 248: 1 249: 1 250: 1 251: 1 252: 1 253: 1 254: 1 255: 1 256: 1 257: 1 258: 1 213 259: 1 213 260: 1 261: 1 213 262: 1 213 263: 1 264: 1 213 265: 1 213 266: 1 213 267: 1 213 268: 1 213 269: 1 48 102 116 213 270: 1 213 271: 1 213 272: 1 213 273: 1 274: 1 275: 1 213 276: 1 213 277: 1 278: 1 279: 1 280: 1 281: 1 213 282: 1 213 283: 1 284: 1 213 285: 1 286: 1 287: 1 213 288: 1 9 73 144 213 289: 1 213 290: 1 213 291: 1 292: 1 213 293: 1 213 294: 1 213 295: 1 213 296: 1 297: 1 298: 1 299: 1 300: 1 301: 1 302: 1 303: 1 304: 1 305: 1 306: 1 307: 1 308: 1 309: 1 Все ОДЛК налицо, все ортогональные пары налицо, осталось взять в руки программу Gephi и нарисовать красивую иллюстрацию. Эх, как бы завтра проснуться и увидеть картинку :) Ладно, я её во сне посмотрю :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Черепашка тоже хочет посмотреть картинку :) Надеюсь, что кто-нибудь в обозримом будущем нам поможет нарисовать картинку. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А это найденная мной рекордная конфигурация 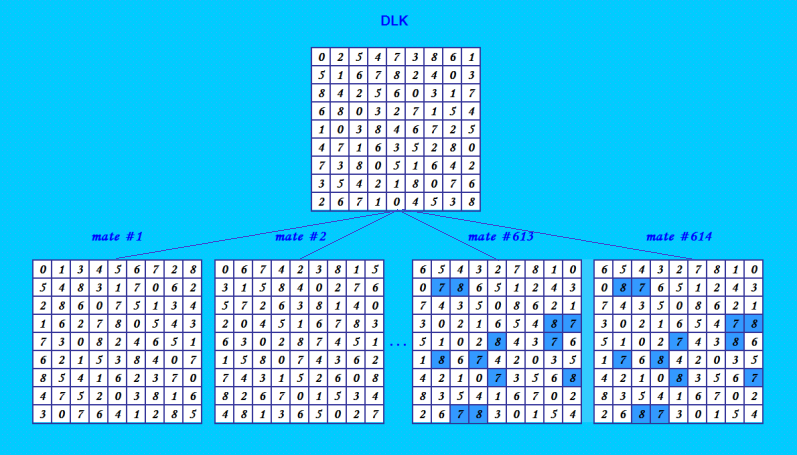 С удивлением обнаружила, что среди 614 ОДЛК нет ни одной ортогональной пары! Order? 9 Enter the name of the squares file: inp ..output file inpPairs_4.txt ..output file inpPairNos_4.txt squares 614 orthogonal pairs 0 Вот такой первый уровень. Собственно, иллюстрация уже показана; правда, из 614 ОДЛК показаны только 4. Ну, все 614 я не могла нарисовать :) Что будет дальше, не проверяла. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
На иллюстрации, показанной в стартовом посте, изображена группа ОДЛК, найденная мной 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 0 1 2 6 7 8 0 1 2 3 4 5 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 0 1 2 3 4 5 6 7 8 6 7 8 0 1 2 3 4 5 3 4 5 6 7 8 0 1 2 5 3 4 8 6 7 2 0 1 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 1 2 0 4 5 3 7 8 6 0 1 2 3 4 5 6 7 8 6 7 8 0 1 2 3 4 5 3 4 5 6 7 8 0 1 2 8 6 7 2 0 1 5 3 4 5 3 4 8 6 7 2 0 1 2 0 1 5 3 4 8 6 7 4 5 3 7 8 6 1 2 0 1 2 0 4 5 3 7 8 6 7 8 6 1 2 0 4 5 3 0 1 2 3 4 5 6 7 8 7 8 6 1 2 0 4 5 3 5 3 4 8 6 7 2 0 1 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 6 7 8 0 1 2 3 4 5 8 6 7 2 0 1 5 3 4 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 0 1 2 3 4 5 6 7 8 7 8 6 1 2 0 4 5 3 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 6 7 8 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 4 5 3 7 8 6 1 2 0 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 5 3 4 8 6 7 2 0 1 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 3 4 5 6 7 8 0 1 2 7 8 6 1 2 0 4 5 3 0 1 2 3 4 5 6 7 8 4 5 3 7 8 6 1 2 0 8 6 7 2 0 1 5 3 4 5 3 4 8 6 7 2 0 1 6 7 8 0 1 2 3 4 5 1 2 0 4 5 3 7 8 6 7 8 6 1 2 0 4 5 3 2 0 1 5 3 4 8 6 7 3 4 5 6 7 8 0 1 2 0 1 2 3 4 5 6 7 8 5 3 4 8 6 7 2 0 1 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 3 4 5 6 7 8 0 1 2 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 4 5 3 7 8 6 1 2 0 6 7 8 0 1 2 3 4 5 0 1 2 3 4 5 6 7 8 5 3 4 8 6 7 2 0 1 7 8 6 1 2 0 4 5 3 4 5 3 7 8 6 1 2 0 6 7 8 0 1 2 3 4 5 2 0 1 5 3 4 8 6 7 8 6 7 2 0 1 5 3 4 1 2 0 4 5 3 7 8 6 3 4 5 6 7 8 0 1 2 0 1 2 3 4 5 6 7 8 8 6 7 2 0 1 5 3 4 4 5 3 7 8 6 1 2 0 2 0 1 5 3 4 8 6 7 7 8 6 1 2 0 4 5 3 3 4 5 6 7 8 0 1 2 1 2 0 4 5 3 7 8 6 6 7 8 0 1 2 3 4 5 5 3 4 8 6 7 2 0 1 Это "перестановочные" ОДЛК, поиском которых занимался проект Rake Search. Там же рисовали и картинки с помощью программы Gephi. Приведённая группа ОДЛК не так проста; я нарисовала иллюстрацию только для ОДЛК в этой замкнутой группе. В группе 10 ОДЛК, вот для них и указаны все ортогональные пары, которые они друг с другом образуют. Если выйти за пределы этой группы, конфигурация значительно расширится; первый ОДЛК этой группы имеет 516 ОДЛК! В проекте Rake Search аналогичную группу ОДЛК представили такой иллюстрацией 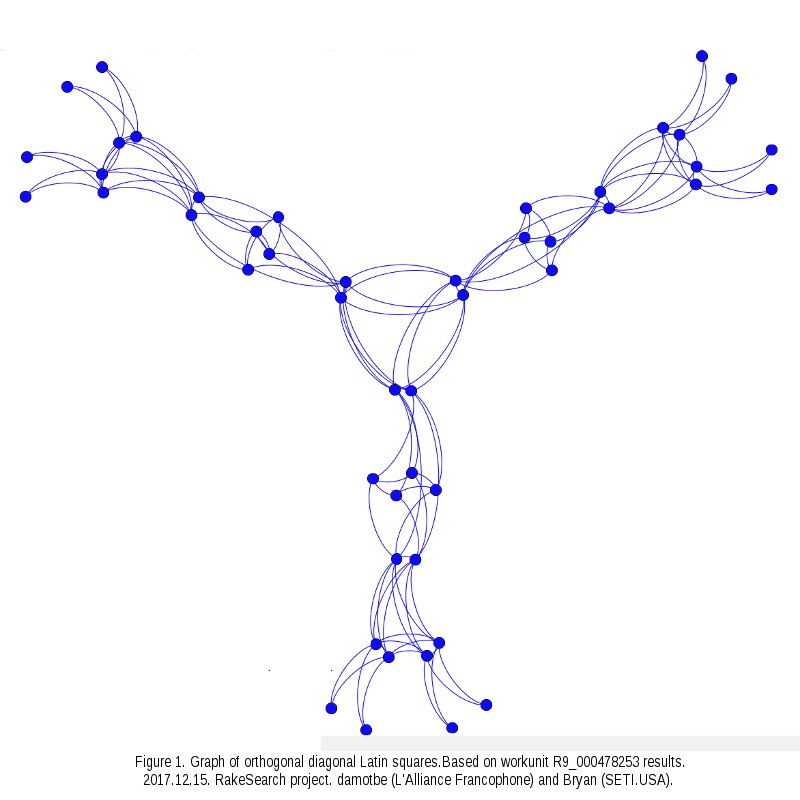 Что-то тут очень мало ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Посмотрим на эту конфигурацию с другой стороны. Первый ОДЛК этой группы имеет 516 ОДЛК. Этот ДЛК входит в полную систему MOLS 9-го порядка  На этой иллюстрации первый ОДЛК группы находится в первом ряду (третий). Вот он [DLK(516):1] 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 0 1 2 6 7 8 0 1 2 3 4 5 7 8 6 1 2 0 4 5 3 1 2 0 4 5 3 7 8 6 4 5 3 7 8 6 1 2 0 5 3 4 8 6 7 2 0 1 8 6 7 2 0 1 5 3 4 2 0 1 5 3 4 8 6 7 Рассмотрим данную конфигурацию. Утилита Harry White находит в группе из 516 ОДЛК 116 ортогональных пар Order? 9 Enter the name of the squares file: inp ..output file inpPairs_4.txt ..output file inpPairNos_4.txt squares 516 orthogonal pairs 116 Замечательно. Таким образом, рассматриваемый квадратик порождает конфигурацию, содержащую 517 ОДЛК (включая его самого) и 632 ортогональные пары. Отличная конфигурация! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Таблица ортогональных пар в группе из 516 ОДЛК, как её выдаёт утилита Harry White 206: 29 318: 60 400: 29 206 424: 60 318 438: 13 14 17 18 19 22 24 29 31 38 43 45 47 48 50 51 53 56 57 58 59 60 61 63 64 65 179 180 190 194 200 201 202 203 204 206 207 208 209 212 215 219 227 245 250 304 308 314 318 325 328 347 380 382 392 394 396 397 398 400 402 403 404 414 416 422 423 424 425 426 427 428 430 431 433 434 435 436 462: 438 466: 438 471: 438 473: 438 474: 438 476: 438 477: 29 206 400 438 478: 438 483: 438 488: 438 490: 438 492: 438 494: 438 500: 438 502: 438 503: 438 504: 438 505: 60 318 424 438 506: 438 507: 438 509: 438 510: 438 511: 438 513: 438 514: 438 516: 438 Здесь 116 ортогональных пар. Добавим в группу исходный ДЛК; получим 517 ОДЛК и 632 ортогональные пары Order? 9 Enter the name of the squares file: inp ..output file inpPairs_5.txt ..output file inpPairNos_5.txt squares 517 orthogonal pairs 632 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, в полной системе MOLS 9-го порядка содержатся шесть ДЛК; все они получаются друг из друга перестановкой строк. И все они ортогональны рассматриваемому ДЛК и потому войдут в порождаемую им конфигурацию. Поэтому мне не совсем понятно, что за конфигурация изображена на иллюстрации с проекта Rake Search. А речь шла именно об этой группе "перестановочных" ОДЛК. По моему мнению конфигурация должна содержать 517 ОДЛК и 632 ортогональные пары. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу совсем простую конфигурацию 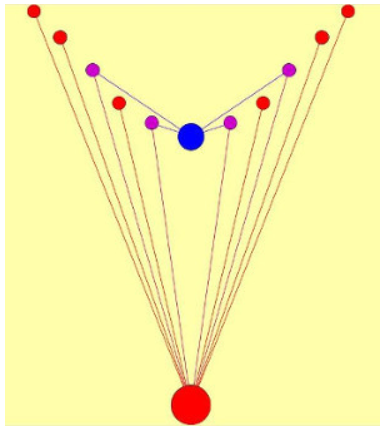 Это моя десяточка (рекордная конфигурация для ОДЛК 10-го порядка). Иллюстрацию рисовал Demis, конечно, вручную. Ну, ничуть не хуже программы Gephi :) Сейчас покажу десяточку; заодно проверю конфигурацию утилитой Harry White - просто для тестирования утилиты. В то время, когда я нашла десяточку, этой утилиты ещё не существовало. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот она - моя десяточка 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 1 4 3 2 3 9 4 1 7 8 0 5 6 9 6 4 5 7 0 1 3 2 8 6 4 1 0 8 3 5 9 7 2 5 9 3 7 2 6 4 8 0 1 1 0 7 8 6 2 3 4 9 5 4 8 6 9 5 1 0 2 3 7 3 5 8 2 9 4 7 6 1 0 7 2 0 1 3 8 9 5 6 4 sq1 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 1 4 3 6 3 9 4 1 7 8 0 5 2 9 2 4 5 7 0 1 3 6 8 2 4 1 0 8 3 5 9 7 6 5 9 3 7 2 6 4 8 0 1 1 0 7 8 6 2 3 4 9 5 4 8 6 9 5 1 0 2 3 7 3 5 8 2 9 4 7 6 1 0 7 6 0 1 3 8 9 5 2 4 sq2 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 2 3 9 4 1 7 8 0 5 6 9 6 4 5 7 0 3 1 2 8 6 4 3 0 8 1 5 9 7 2 5 9 1 7 2 6 4 8 0 3 3 0 7 8 6 2 1 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 8 2 9 4 7 6 3 0 7 2 0 1 3 8 9 5 6 4 sq3 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 6 3 9 4 1 7 8 0 5 2 9 2 4 5 7 0 3 1 6 8 2 4 3 0 8 1 5 9 7 6 5 9 1 7 2 6 4 8 0 3 3 0 7 8 6 2 1 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 8 2 9 4 7 6 3 0 7 6 0 1 3 8 9 5 2 4 sq4 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 1 4 3 2 3 9 4 1 7 8 0 5 6 9 6 4 5 7 8 1 3 2 0 6 4 1 0 8 3 5 9 7 2 5 9 3 7 2 6 4 8 0 1 1 0 7 8 6 2 3 4 9 5 4 8 6 9 5 1 0 2 3 7 3 5 0 2 9 4 7 6 1 8 7 2 8 1 3 0 9 5 6 4 sq5 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 1 4 3 6 3 9 4 1 7 8 0 5 2 9 2 4 5 7 8 1 3 6 0 2 4 1 0 8 3 5 9 7 6 5 9 3 7 2 6 4 8 0 1 1 0 7 8 6 2 3 4 9 5 4 8 6 9 5 1 0 2 3 7 3 5 0 2 9 4 7 6 1 8 7 6 8 1 3 0 9 5 2 4 sq6 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 2 3 9 4 1 7 8 0 5 6 9 6 4 5 7 8 3 1 2 0 6 4 3 0 8 1 5 9 7 2 5 9 1 7 2 6 4 8 0 3 3 0 7 8 6 2 1 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 0 2 9 4 7 6 3 8 7 2 8 1 3 0 9 5 6 4 sq7 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 6 3 9 4 1 7 8 0 5 2 9 2 4 5 7 8 3 1 6 0 2 4 3 0 8 1 5 9 7 6 5 9 1 7 2 6 4 8 0 3 3 0 7 8 6 2 1 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 0 2 9 4 7 6 3 8 7 6 8 1 3 0 9 5 2 4 sq8 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 2 3 9 4 8 7 1 0 5 6 9 6 4 5 7 1 3 8 2 0 6 4 3 0 1 8 5 9 7 2 5 9 8 7 2 6 4 1 0 3 3 0 7 1 6 2 8 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 0 2 9 4 7 6 3 8 7 2 1 8 3 0 9 5 6 4 sq9 0 1 2 3 4 5 6 7 8 9 8 7 5 6 0 9 2 3 4 1 6 3 9 4 8 7 1 0 5 2 9 2 4 5 7 1 3 8 6 0 2 4 3 0 1 8 5 9 7 6 5 9 8 7 2 6 4 1 0 3 3 0 7 1 6 2 8 4 9 5 4 8 6 9 5 3 0 2 1 7 1 5 0 2 9 4 7 6 3 8 7 6 1 8 3 0 9 5 2 4 sq10 Square: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 3 7 9 6 8 9 7 6 2 3 8 5 1 4 0 7 5 1 8 6 9 2 0 3 4 3 9 8 6 7 4 1 2 0 5 2 4 5 9 8 1 0 3 7 6 4 8 3 0 2 6 9 5 1 7 8 6 7 5 9 0 3 4 2 1 6 3 9 1 0 7 4 8 5 2 5 0 4 7 1 2 8 6 9 3 отсюда https://boinc.progger.info/odlk/forum_thread.php?id=1&postid=1742 Ввожу эту группу ОДЛК в программу Harry White, она выдаёт Order? 10 Enter the name of the squares file: inp ..output file inpPairs_1.txt ..output file inpPairNos_1.txt squares 11 orthogonal pairs 10 Всё верно, в этой группе только 10 ортогональных пар. Это первый уровень. Далее идёт второй уровень: появился новый ОДЛК и 4 новые ортогональные пары. Это полная конфигурация, порождаемая основным ДЛК десяточки, она и изображена на иллюстрации. PS. Это основной ДЛК десяточки (на иллюстрации большой красный кружок) Square: 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 3 7 9 6 8 9 7 6 2 3 8 5 1 4 0 7 5 1 8 6 9 2 0 3 4 3 9 8 6 7 4 1 2 0 5 2 4 5 9 8 1 0 3 7 6 4 8 3 0 2 6 9 5 1 7 8 6 7 5 9 0 3 4 2 1 6 3 9 1 0 7 4 8 5 2 5 0 4 7 1 2 8 6 9 3 ОДЛК, появившийся на втором уровне, синий кружочек на иллюстрации. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Господа! Я вас всё ещё не заинтересовала? :) Вы ещё не рисуете? И программу Gephi ещё не скачали? :) Плохой я популяризатор! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Хорошо, покажу ещё одну интересную конфигурацию для ОДЛК 10-го порядка. Цитата отсюда https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=2958 В автономном подпроекте в эксперименте по поиску решений с симметрией (4,31,31) по алгоритму Белышева Tomas Brada нашёл восьмёрку с данной симметрией, которая порождает очень интересную конфигурацию Разберётесь без комментариев? Если есть вопросы, пожалуйста, спрашивайте, не стесняйтесь. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Черепашка рисует :) конфигурация, показанная в предыдущем посте 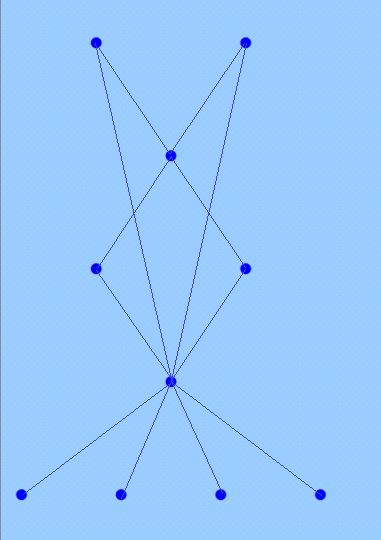 Как? Ничего? :) Черепашка у меня молодец! Но вот сотни точек и сотни линий трудно черепашке нарисовать без программы. PS. Может быть, самые верхние две точки надо немножко подальше друг от друга сделать, чтобы изменить угол рёбер графов. Ну, черепашка ещё только учится :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Повторю конфигурацию, которую нарисовала в предыдущем посте 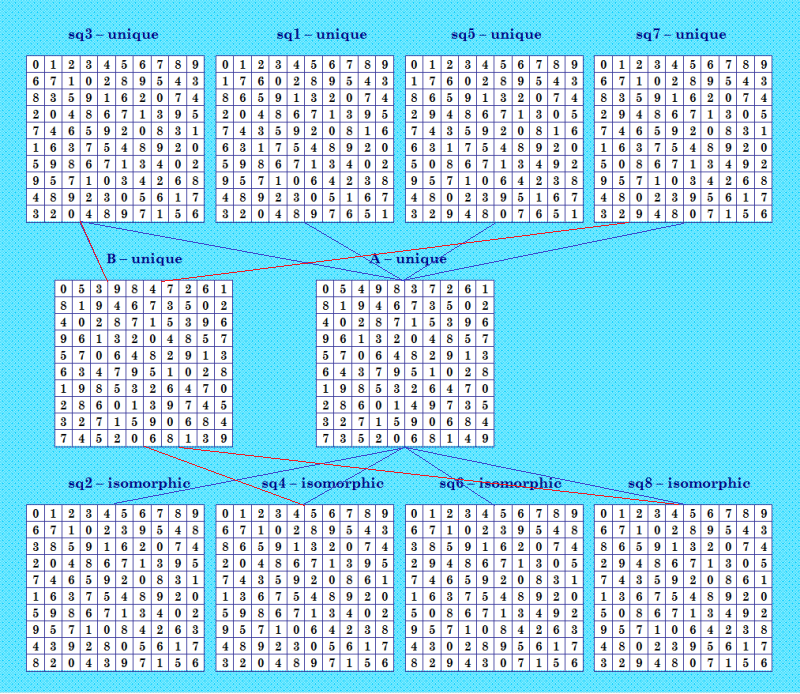 Хочу показать таблицу ортогональных пар для этой конфигурации. Квадраты пронумерую по показанной иллюстрации сверху вниз, слева направо: sq3 - 1, sq1 - 2 и т. д. Всего в конфигурации 10 ОДЛК. Я ввела их в программу Harry White прямо с этой иллюстрации. Вот таблица ортогональных пар, выданная программой 5: 1 4 6: 1 2 3 4 7: 6 8: 5 6 9: 6 10: 5 6 Всё верно, легко проверить по иллюстрации. В конфигурации 12 ортогональных пар. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У этого квадратика 9-го порядка [DLK(329):49039] 0 2 5 4 6 3 7 8 1 3 1 4 6 5 8 2 0 7 4 8 2 1 7 6 3 5 0 7 4 0 3 8 2 5 1 6 8 7 6 5 4 0 1 3 2 6 0 1 7 2 5 8 4 3 1 5 8 0 3 7 6 2 4 2 6 3 8 0 1 4 7 5 5 3 7 2 1 4 0 6 8 интересная конфигурация первого уровня. Среди 329 ОДЛК есть всего 8 ортогональных пар 277: 101 279: 101 281: 101 283: 101 311: 101 313: 101 328: 101 329: 101 Следовательно, вся конфигурация первого уровня содержит 330 ОДЛК (включая исходный ДЛК) и 337 ортогональных пар. Сейчас попробую нарисовать эту конфигурацию. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У меня такая иллюстрация получилась 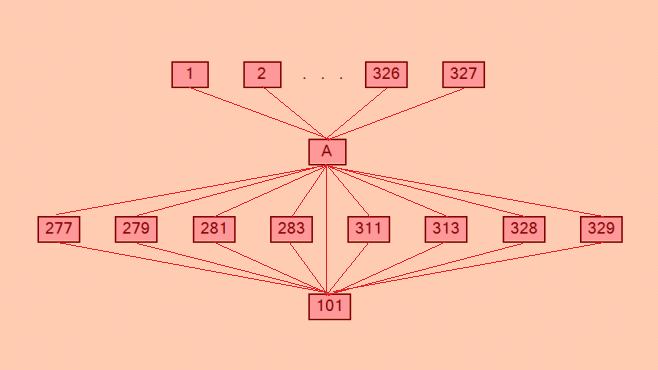 Понятно, что в верхнем ряду должны быть изображены все квадраты от 1 до 327, исключая квадраты: 101, 277, 279, 281, 283, 311, 313. Я изобразила только 4 квадрата. Квадрат А - основной ДЛК, порождающий данную конфигурацию. Напомню: это только первый уровень. Очень возможно, что от 329 ОДЛК потянутся новые ветви. Интересно в этой конфигурации наблюдать тройки MODLS. Их восемь: А, 101, 277; А, 101, 279; ... А, 101, 329. Отмечу, что конфигурация содержит 116 уникальных ОДЛК, как утверждает канонизатор Harry White Order? 9 Format, (1: first row or 2: \diagonal)? 2 File name? inp .. writing DLS to file output9CF2_1.txt number of DLS 330 CFs 116 И наконец, покажу типы квадратов конфигурации Order? 9
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
330 diagonal Latin
2 center symmetric
1 natural \diagonal
1 orthogonal pair
45 self-orthogonalОсновной ДЛК, порождающий конфигурацию, является SODLS. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот, мы с черепашкой работаем за программу Gephi :) Конечно, не так красиво, но наглядность есть, что и требуется от подобных иллюстраций. Ой, заглянула в поиск Яндекса, там даже предлагается скачать Gephi на русском. Всё ещё не отважилась скачать :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нам с черепашкой сегодня очень хочется рисовать :) Посему ещё одна конфигурация ОДЛК 9-го порядка, порождаемая этим квадратиком [DLK(310):113250] 0 3 5 4 6 7 8 2 1 8 1 7 5 3 4 2 0 6 6 4 2 8 7 0 3 1 5 7 8 1 3 0 6 4 5 2 3 5 0 2 4 8 1 6 7 2 6 4 7 1 5 0 8 3 1 7 8 0 5 2 6 3 4 4 2 6 1 8 3 5 7 0 5 0 3 6 2 1 7 4 8 Квадратик даёт 310 ОДЛК. Среди этих 310 ОДЛК утилита Harry White нашла 20 ортогональных пар 131: 1 270: 1 131 303: 1 131 270 304: 131 306: 131 304 308: 131 304 306 309: 1 131 270 303 310: 131 304 306 308 Значит, всего в конфигурации первого уровня содержится 311 ОДЛК и 330 ортогональных пар. Сейчас мы с черепашкой будем рисовать эту конфигурацию. Сначала подумаем, как расположить 20 ортогональных пар. Господа! Присоединяйтесь к нам! Не хотите программу Gephi задействовать, рисуйте как-то по-другому. Можно и не совсем вручную, как мы с черепашкой рисуем. Вот друг, к примеру, написал какой-то свой скрипт. Ой, я его сейчас и покажу даже - этот скрипт. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger