Отличная новость от Harry White.
Цитирую

I installed 32 and 64 bit canonizers for orders 4 .. 15.

http://budshaw.ca/Download.html#canonizer

http://budshaw.ca/Download.html#canonizer64

Also GetDiagonals just above the canonizers.

The canonizer code is tidied up some and comments are added.
You may now throw away the old code and programs.

Канонизаторы ДЛК до порядка 15 включительно!
Грандиозно!!
Ещё программа для извлечения из КФ уникальных побочных диагоналей (=линеек).
Как я понимаю, есть коды всех программ.

Огромная благодарность Harry!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Попробовала канонизатор Harry для ДЛК 14-го порядка

Order? 14
Format, (1: first row or 2: \diagonal)? 2
File name? INP
.. writing DLS to file output14CF2.txt
number of DLS 290 CFs 290

elapsed time 0:00:06

Супер!
Все ОДЛК набора уникальные.
Покажу первые две КФ ОДЛК (формат 2)

 0  2  3  5 11  4 13 12 10  7  6  8  9  1
13  1  5  8  2  7 12  9  4  3 11 10  0  6
 8  6  2 12  7 10  0  1 11 13  9  3  5  4
 5 12 10  3  9  8  4 11  0  6  2 13  1  7
10  7  8 11  4  0  9  6 13  5 12  1  2  3
11 13  1  6 10  5  7  4  9 12  8  0  3  2
 2  9 11  4  5  3  6  8  1 10 13 12  7  0
12  3 13  2  1 11 10  7  5  4  0  9  6  8
 7 10  4  9  0 12  3 13  8  2  1  6 11  5
 1  8 12  0 13  2  5 10  6  9  3  7  4 11
 3  4  0  7  6  1 11  5 12  8 10  2 13  9
 9  5  6  1  8 13  2  3  7  0  4 11 10 12
 6 11  7 13  3  9  8  0  2  1  5  4 12 10
 4  0  9 10 12  6  1  2  3 11  7  5  8 13

 0  2  4  8  3 10  5 13  7 12  6  9 11  1
 7  1  8  2 13  4 12 11  5  6  3 10  0  9
12 13  2 10 11  1  0  6  9  4  5  3  7  8
 1 12  6  3 10  7  9  2 13 11  4  0  8  5
13 10  3 12  4  8  1  0  6  5  9  7  2 11
11  6  1  7  8  5  3  9 10  2 13 12  4  0
 3  4 10 13  9 11  6  8  1  0  7  2  5 12
 4  8  9  5  1  0 11  7 12 10  2 13  3  6
 5 11  7  9  0 12  2 10  8  3  1  6 13  4
10  0  5 11  2  6 13  4  3  9 12  8  1  7
 8  3  0  6  5 13  4 12 11  7 10  1  9  2
 6  9 13  4 12  2  7  5  0  1  8 11 10  3
 2  7 11  1  6  9  8  3  4 13  0  5 12 10
 9  5 12  0  7  3 10  1  2  8 11  4  6 13

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Хм... Полученные КФ ОДЛК находятся в 273 линейках

Order? 14
File? inp
Input file is inp.txt
.. writing squares to file inpDiags.txt
Which \ 1 or / 2? 2
squares 290 diags 273

Отличный охват!

Тэк-с... а сколько всего линеек для СН ДЛК 14-го порядка???
273 линейки я уже получила.
Первые 10 линеек выглядят так

 1  0  3  2  5  4  8 10  7 11  6 12 13  9
 1  0  3  2  5  4  8 10 12  7 13  6  9 11
 1  0  3  2  5  4  8 10 12  7 13  9 11  6
 1  0  3  2  5  6  4 10 11 12  9  8 13  7
 1  0  3  2  5  6  4 10 11 12  9 13  7  8
 1  0  3  2  5  6  4 10 11 12 13  7  8  9
 1  0  3  2  5  6  8  4  9 10 12 13 11  7
 1  0  3  2  5  6  8  9 10 11 12 13  4  7
 1  0  3  2  5  6  8 10  4 11  9 12 13  7
 1  0  3  2  5  6  8 10  9 11 12 13  4  7

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Набор из 290 КФ ОДЛК 14-го порядка я получила от ДЛК, построенного методом Гергели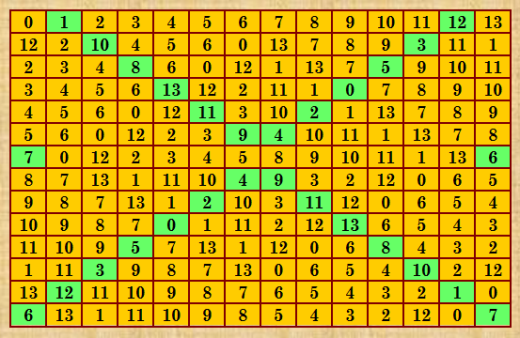



Но это не все ОДЛК, программу проверки на марьяжность я прервала, покрутив её 12 часов

Проверка ДЛК14 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 364252
Соквадратов:     290
Время в сек:     43755

25632 10343 3872 1100 41 79 2   2

Это давно я проверяла.
Конечно, тут ещё будут ОДЛК и, наверное, много.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

О-о-о!
А если добавить в набор сам квадрат Гергели, получается 274 линейки!

Order? 14
File? Inp
Input file is Inp.txt
.. writing squares to file InpDiags_1.txt
Which \ 1 or / 2? 2
squares 291 diags 274

Вот как интересно!
Итак, у меня есть уже 274 линейки для СН ДЛК 14-го порядка.

А это КФ квадрата Гергели, формат 2

 0  7  8 13  9  3  4  5  2 12 11  6 10  1
 8  1 11  4  7  9  2  3 12 10  5 13  0  6
 4 13  2 12  8  1  7 10  0  6  9  3 11  5
13  8  4  3  1  7 12  9 10  0  2  5  6 11
 9  3  7  1  4 11  8  6 13  5  0 10  2 12
 7 12  1  8  3  5 13 11  4  2  6  0  9 10
12  2 10  0  5 13  6  8 11  4  1  7  3  9
 5 11  3  9  6  0 10  7  1  8 12  2 13  4
 2  4 12 10 13  6  0  1  8 11  7  9  5  3
 1 10  6 11 12  2  5  4  3  9 13  8  7  0
 3  5  9  7 11  8  1  0  6 13 10 12  4  2
 6  0 13  5 10 12  3  2  9  7  4 11  1  8
10  9  0  6  2  4 11 13  5  3  8  1 12  7
11  6  5  2  0 10  9 12  7  1  3  4  8 13

Красавчик! Симметричный по Гергели/Брауну, да ещё и "браун".

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Однако не забываем, что порядок 14 сильно проблемный, он из серии порядков n=4k+2, из этой же серии порядок 10.
Ассоциативных ДЛК 14-го порядка не существует, как и любого порядка данной серии.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверила бегло другие ЛК из группы MOLS 12-го порядка.
Как и предполагалось, они все дают в результате перестановки строк крутые ДЛК.

Так, от ЛК №3 получен ДЛК с 24731 Д-трансверсалей,
от ЛК №4 - с 24764 Д-трансверсалей,
от ЛК №5 - с 24356 Д-трансверсалей.

Затем получила от ЛК №4 пять других ДЛК (можно и больше получить).
Среди них есть ДЛК с 24869 и 24901 Д-трансверсалей, вот они

0 8 1 B 5 9 3 A 2 7 6 4
B 1 6 4 A 2 8 3 7 0 5 9
1 9 2 6 0 A 4 B 3 8 7 5
4 6 5 9 3 7 1 8 0 B A 2
9 5 A 2 8 0 6 1 B 4 3 7
7 3 8 0 6 4 A 5 9 2 1 B
2 A 3 7 1 B 5 6 4 9 8 0
3 B 4 8 2 6 0 7 5 A 9 1
A 0 B 3 9 1 7 2 6 5 4 8
8 4 9 1 7 5 B 0 A 3 2 6
5 7 0 A 4 8 2 9 1 6 B 3
6 2 7 5 B 3 9 4 8 1 0 A
24869 Д-трансверсалей

0 8 1 B 5 9 3 A 2 7 6 4
5 7 0 A 4 8 2 9 1 6 B 3
2 A 3 7 1 B 5 6 4 9 8 0
4 6 5 9 3 7 1 8 0 B A 2
3 B 4 8 2 6 0 7 5 A 9 1
7 3 8 0 6 4 A 5 9 2 1 B
8 4 9 1 7 5 B 0 A 3 2 6
9 5 A 2 8 0 6 1 B 4 3 7
A 0 B 3 9 1 7 2 6 5 4 8
1 9 2 6 0 A 4 B 3 8 7 5
B 1 6 4 A 2 8 3 7 0 5 9
6 2 7 5 B 3 9 4 8 1 0 A
24901 Д-трансверсалей

Так что, работы с этими ДЛК непочатый край.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для порядка 15 у меня есть построенная мной группа из четырёх взаимно ортогональных ДЛК.
Эти ДЛК показаны на иллюстрациях здесь
https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5717
и в следующем посте.
Сейчас я их канонизирую, чтобы опробовать канонизатор Harry White.
Интересно посмотреть на КФ ОДЛК 15-го порядка!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Готово!

Order? 15
Format, (1: first row or 2: \diagonal)? 2
File name? inp
.. writing DLS to file output15CF2.txt
number of DLS 4 CFs 4

Все 4 ОДЛК уникальные.
Вот эти 4 КФ ОДЛК

 0  5  4 12 14 11  8  2  9 13  7 10  6  3  1
14  1  6  5 11 13 10  3 12  7  9  0  4  2  8
 9 13  2  0  6 10 12  4  7  8  1  5  3 14 11
11  8 12  3  1  0  9  5 14  2  6  4 13 10  7
 8 10 14 11  4  2  1  6  3  0  5 12  9  7 13
 2 14  9 13 10  5  3  0  1  6 11  8  7 12  4
 4  3 13  8 12  9  6  1  0 10 14  7 11  5  2
 5  6  0  1  2  3  4  7 10 11 12 13 14  8  9
12  9  3  7  0  4 14 13  8  5  2  6  1 11 10
10  2  7  6  3  8 13 14 11  9  4  1  5  0 12
 1  7  5  2  9 14 11  8 13 12 10  3  0  4  6
 7  4  1 10  8 12  0  9  5 14 13 11  2  6  3
 3  0 11  9 13  6  7 10  2  4  8 14 12  1  5
 6 12 10 14  5  7  2 11  4  1  3  9  8 13  0
13 11  8  4  7  1  5 12  6  3  0  2 10  9 14

 0  7  9 12  8  6  2 11 10  3  4 14 13  5  1
 3  1  7  8 11 14  0 10  4  5 13 12  6  2  9
 1  4  2  7 14 10 13  9  6 12 11  0  3  8  5
12  2  5  3  7 13  9  8 11 10  1  4 14  6  0
 8 11  3  6  4  7 12 14  9  2  5 13  0  1 10
11 14 10  4  0  5  7 13  3  6 12  1  2  9  8
 7 10 13  9  5  1  6 12  0 11  2  3  8 14  4
 2  3  4  5  6  0  1  7 13 14  8  9 10 11 12
10  0  6 11 12  3 14  2  8 13  9  5  1  4  7
 6  5 12 13  2  8 11  1  7  9 14 10  4  0  3
 4 13 14  1  9 12  5  0  2  7 10  8 11  3  6
14  8  0 10 13  4  3  6  5  1  7 11  9 12  2
 9  6 11 14  3  2  8  5  1  4  0  7 12 10 13
 5 12  8  2  1  9 10  4 14  0  3  6  7 13 11
13  9  1  0 10 11  4  3 12  8  6  2  5  7 14

 0  8  5  7  2 14 11  3  9  4 13  6 10 12  1
10  1 14  6  7  3 13  4  5 12  0  9 11  2  8
12  9  2 13  0  7  4  5 11  1  8 10  3 14  6
 5 11  8  3 12  1  7  6  2 14  9  4 13  0 10
 7  6 10 14  4 11  2  0 13  8  5 12  1  9  3
 3  7  0  9 13  5 10  1 14  6 11  2  8  4 12
 9  4  7  1  8 12  6  2  0 10  3 14  5 11 13
14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
 1  3  9  0 11  4 14 12  8  2  6 13  7 10  5
 2 10  6 12  3  8  0 13  4  9  1  5 14  7 11
11  5 13  2  9  6  1 14 12  3 10  0  4  8  7
 4 14  1 10  5  0 12  8  7 13  2 11  6  3  9
 8  0 11  4  6 13  3  9 10  7 14  1 12  5  2
 6 12  3  5 14  2  9 10  1 11  7  8  0 13  4
13  2  4  8  1 10  5 11  3  0 12  7  9  6 14

 0  8 13  7  6  9  4 12 11  2 14 10  5  3  1
 5  1 14 12  7  0  8 11  3 13  9  6  4  2 10
14  6  2 13 11  7  1 10 12  8  0  5  3  9  4
 2 13  0  3 12 10  7  9 14  1  6  4  8  5 11
 7  3 12  1  4 11  9  8  2  0  5 14  6 10 13
 8  7  4 11  2  5 10 14  1  6 13  0  9 12  3
 9 14  7  5 10  3  6 13  0 12  1  8 11  4  2
 6  0  1  2  3  4  5  7  9 10 11 12 13 14  8
12 10  3  6 13  2 14  1  8 11  4  9  7  0  5
11  2  5 14  1  8 13  0  4  9 12  3 10  7  6
 1  4  8  0  9 14 12  6  5  3 10 13  2 11  7
 3  9  6 10  8 13  0  5  7  4  2 11 14  1 12
10  5 11  9 14  6  2  4 13  7  3  1 12  8  0
 4 12 10  8  5  1 11  3  6 14  7  2  0 13  9
13 11  9  4  0 12  3  2 10  5  8  7  1  6 14

Подчеркну ещё раз: это группа MODLS, то есть все ДЛК в этой группе взаимно ортогональны.
Здесь интересная задача: можно ли расширить эту группу MODLS до 5 ОДЛК?

PS. Все эти 4 КФ ОДЛК находятся в одной линейке

1  2  3  4  5  6  0  7 14  8  9 10 11 12 13

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

И проверка этих 4-х КФ ОДЛК утилитой Harry White

Order? 15

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt

Counts
------
         4 diagonal Latin
         4 associative
         4 natural \diagonal

Странно: почему здесь не найдена ортогональная пара? Ведь два ортогональных ДЛК рядом есть, причём не один раз.

Проверила своей программой ортогональность КФ ОДЛК, нет ортогональности!
Но почему?
Исходные ДЛК ортогональные!
Вот они

1 7 12 10 9 3 15 8 2 14 11 4 13 5 6
3 2 8 13 11 10 4 9 1 12 5 14 6 7 15
2 4 3 9 14 12 11 10 13 6 1 7 8 15 5
14 3 5 4 10 1 13 11 7 2 8 9 15 6 12
8 1 4 6 5 11 2 12 3 9 10 15 7 13 14
4 9 2 5 7 6 12 13 10 11 15 8 14 1 3
11 5 10 3 6 8 7 14 12 15 9 1 2 4 13
9 10 11 12 13 14 1 15 8 7 6 5 4 3 2
6 11 9 8 2 15 5 7 14 1 13 10 3 12 4
10 8 7 1 15 4 3 6 5 13 14 12 9 2 11
7 6 14 15 3 2 10 5 9 4 12 13 11 8 1
5 13 15 2 1 9 14 4 6 8 3 11 12 10 7
12 15 1 14 8 13 6 3 4 5 7 2 10 11 9
15 14 13 7 12 5 8 2 11 3 4 6 1 9 10
13 12 6 11 4 7 9 1 15 10 2 3 5 14 8

1 11 8 3 6 12 9 14 7 2 10 5 15 13 4
8 2 12 9 4 7 13 1 3 11 6 15 14 5 10
4 9 3 13 10 5 8 2 12 7 15 1 6 11 14
13 5 10 4 14 11 6 3 8 15 2 7 12 1 9
9 14 6 11 5 1 12 4 15 3 8 13 2 10 7
15 10 1 7 12 6 2 5 4 9 14 3 11 8 13
5 15 11 2 8 13 7 6 10 1 4 12 9 14 3
12 13 14 1 2 3 4 15 11 10 9 8 7 6 5
10 7 2 5 11 8 3 13 14 6 1 9 4 15 12
6 1 4 10 7 2 11 12 9 13 5 14 8 3 15
14 3 9 6 1 10 15 11 5 8 12 4 13 7 2
2 8 5 14 9 15 1 10 13 4 7 11 3 12 6
7 4 13 8 15 14 5 9 1 12 3 6 10 2 11
3 12 7 15 13 4 10 8 6 14 11 2 5 9 1
11 6 15 12 3 9 14 7 2 5 13 10 1 4 8
 
1 9 7 13 3 2 12 5 8 15 4 14 11 6 10
9 2 10 8 14 4 3 6 15 5 1 12 7 11 13
15 10 3 11 9 1 5 7 6 2 13 8 12 14 4
7 15 11 4 12 10 2 8 3 14 9 13 1 5 6
4 8 15 12 5 13 11 9 1 10 14 2 6 7 3
2 5 9 15 13 6 14 10 11 1 3 7 8 4 12
12 3 6 10 15 14 7 11 2 4 8 9 5 13 1
14 1 2 3 4 5 6 15 13 12 11 10 9 8 7
8 6 12 2 1 11 9 4 14 7 15 3 13 10 5
5 11 1 14 10 8 4 3 7 13 6 15 2 12 9
10 14 13 9 7 3 8 2 4 6 12 5 15 1 11
13 12 8 6 2 7 10 1 9 3 5 11 4 15 14
11 7 5 1 6 9 13 14 12 8 2 4 10 3 15
6 4 14 5 8 12 15 13 10 11 7 1 3 9 2
3 13 4 7 11 15 1 12 5 9 10 6 14 2 8

1 6 13 7 12 5 8 3 9 10 15 2 4 11 14
10 2 7 14 8 13 6 4 11 15 3 5 12 1 9
12 11 3 8 1 9 14 5 15 4 6 13 2 10 7
15 13 12 4 9 2 10 6 5 7 14 3 11 8 1
6 15 14 13 5 10 3 7 8 1 4 12 9 2 11
9 7 15 1 14 6 11 8 2 5 13 10 3 12 4
3 10 8 15 2 1 7 9 6 14 11 4 13 5 12
13 14 1 2 3 4 5 15 12 11 10 9 8 7 6
5 12 6 11 4 7 13 2 14 8 9 15 1 3 10
11 5 10 3 6 12 9 1 4 13 7 8 15 14 2
4 9 2 5 11 8 1 14 10 3 12 6 7 15 13
8 1 4 10 7 14 12 13 3 9 2 11 5 6 15
14 3 9 6 13 11 15 12 7 2 8 1 10 4 5
2 8 5 12 10 15 4 11 13 6 1 7 14 9 3
7 4 11 9 15 3 2 10 1 12 5 14 6 13 8

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверяю исходные ДЛК утилитой Harry White

Order? 15

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt

Counts
------
         4 diagonal Latin
         4 center symmetric
         3 orthogonal pair

Здесь ортогональные пары найдены.

Я пока ничего не понимаю.
Группа 4-х ОДЛК (взаимно ортогональных) есть.
А КФ этих ОДЛК друг другу не ортогональны... Это правильно?
Наверное, вчерашний ливень на меня плохо повлиял :)

Действительно, кажется, перегрелась :)
Взяла ортогональную пару 11-го порядка, канонизировала ОДЛК, проверила КФ этих ОДЛК, они не ортогональны.

Да, вспоминаю, как писал великий теоретик Белышев: ортогональны классы эквивалентности, которые представляются данными КФ.
В одном классе есть один ДЛК ортогональной пары, в другом классе - второй ДЛК ортогональной пары.

Ох, весь век учись и дураком помрёшь! Точная поговорка :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Тэк-с, мозги вроде встали на место :)
Ой, а за окном опять туча заходит! Этот дождь все мозги мне размочил :)
Уже льёт, с грозой!

Пытаюсь найти ещё линейки для СН ДЛК 14-го порядка.
Плохо получается, мало у меня КФ, всего 4070 на данный момент, а линеек они представляют 278

Order? 14
File? inp
Input file is inp.txt
.. writing squares to file inpDiags_2.txt
Which \ 1 or / 2? 2
squares 4070 diags 278

Всего 4 новые линейки добавились.
Надо много КФ сгенерировать, тогда дело продвинется.
Но у меня нет генератора для СН ДЛК 14-го порядка.
Понятно, что генерировать ДЛК надо по такому паттерну

0 X X X X X X X X X X X X 1
X 1 X X X X X X X X X X X X
X X 2 X X X X X X X X X X X
X X X 3 X X X X X X X X X X
X X X X 4 X X X X X X X X X
X X X X X 5 X X X X X X X X
X X X X X X 6 X X X X X X X
X X X X X X X 7 X X X X X X
X X X X X X X X 8 X X X X X
X X X X X X X X X 9 X X X X
X X X X X X X X X X 10 X X X
X X X X X X X X X X X 11 X X
X X X X X X X X X X X X 12 X
X X X X X X X X X X X X X 13

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Harry White сделал по моей просьбе программу поиска в наборе ОДЛК ортогональных пар.
Цитата

Program GetOrthogonal is installed just above
http://budshaw.ca/Download.html#canonizer

Очень полезная программа для поиска групп MODLS.

Алгоритм мне видится такой: для некоторого ДЛК находим все ортогональные диагональные соквадраты.
Затем в этом наборе ОДЛК ищем программой Harry ортогональные пары.
Если хотя бы одна ортогональная пара найдена, то найдена тройка MODLS.

Я уже проверила работу программы на нескольких наборах ОДЛК разных порядков.
Расскажу об этом чуть позже.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Итак, первый проверенный на ортогональные пары набор ОДЛК 9-го порядка, состоящий из 516 ОДЛК.
Протокол работы программы Harry White GetOrthogonal

Order? 9

Enter the name of the squares file: inp
..output file inpPairs.txt
..output file inpPairNos.txt
squares 516 orthogonal pairs 116

В наборе найдено 116 ортогональных пар.

Вывод программы

100:  52
344:  15
380:  7 8 9 11 12 13 14 15 16 18
 19 21 22 34 36 37 39 43 44 46
 48 52 53 57 67 68 84 85 91 93
 96 97 98 100 101 103 104 105 106 281
 282 296 297 304 308 310 343 344 350 353
 374 377
384:  380
385:  380
388:  380
389:  380
390:  380
392:  380
393:  380
394:  15 344 380
395:  380
396:  380
397:  380
399:  380
400:  380
403:  380
404:  380
407:  380
408:  380
413:  380
420:  380
424:  380
425:  380
427:  380
428:  380
435:  52 100 380
437:  380
439:  380
449:  380
450:  380
458:  380
460:  380
462:  380
463:  380
465:  380
467:  380
469:  380
473:  52 100 380 435
474:  380
478:  380
480:  380
485:  380
486:  380
488:  380
490:  380
491:  380
492:  380
493:  15 344 380 394
494:  380
495:  380
499:  380
500:  380
501:  380
502:  380

Интересно!
Здесь можно найти полную систему MODLS 9-го порядка, если добавить сюда исходный ДЛК.
Кстати, исходный ДЛК взят из полной системы MOLS 9-го порядка.

Далее проверила набор ОДЛК 11-го порядка, состоящий из 26914 ОДЛК.
Исходный ДЛК взят из полной системы MOLS 11-го порядка.
Протокол этой проверки

Order? 11

Enter the name of the squares file: inp
..output file inpPairs.txt
..output file inpPairNos.txt
squares 26914 orthogonal pairs 186

elapsed time 0:02:00

Здесь найдено 186 ортогональных пар.
Вывод программы

6423:  1800
11107:  1800 6423
11489:  1800 6423 11107
18550:  453 454 457 463 464 465 466 467 470 471
 492 493 499 517 531 1690 1749 1800 4891 4901
 4906 4908 4909 4917 4920 4921 4953 4954 4957 4958
 4959 4963 4964 6362 6419 6423 9131 9132 9138 9156
 9157 9158 9163 9177 9179 9183 9189 9207 9208 9210
 9211 11060 11102 11107 11180 11181 11186 11188 11190 11191
 11202 11203 11220 11234 11235 11250 11259 11260 11261 11477
 11487 11489 11536 11558 11581 11724 11725 11727 11728 11731
 11732 11735 11739 11749 11782 11795 11796 11798 11805 11806
 12069 12079 12080 12081 12085 12086 12099 12102 12107 12108
 12116 12117 12136 12137 12144 13240 13241 13242 13246 13247
 13258 13263 13264 13271 13276 13277 13281 13282 13283 13317
 14627 14628 14651 14653 14654 14656 14659 14660 14679 14680
 14691 14693 14695 14702 14704
19547:  18550
19561:  1800 6423 11107 11489 18550
19682:  18550
20696:  18550
20722:  18550
20723:  18550
20740:  18550
20741:  18550
20742:  18550
20750:  18550
20751:  18550
20754:  18550
20759:  18550
20761:  18550
20768:  18550
20773:  18550
20774:  18550
20777:  18550
24784:  1800 6423 11107 11489 18550 19561
24786:  18550
24795:  18550
26378:  18550
26383:  18550
26390:  18550
26393:  18550
26394:  18550
26396:  18550
26398:  18550
26401:  18550
26403:  18550
26407:  18550
26408:  18550
26426:  18550
26427:  18550
26428:  18550
26448:  18550

Не анализировала тут взаимно ортогональные ДЛК.
Думаю, что полная система MODLS 11-го порядка здесь содержится.

Далее проверила набор ОДЛК 12-го порядка, полученный от ДЛК, построенного методом Гергели. Этот набор содержит 2199 ОДЛК.
Ортогональных пар в нём не найдено.

И здесь мы вплотную подошли к задаче поиска тройки MODLS 12-го порядка.
Согласно показанной выше теореме может существовать даже группа из 5 MODLS 12-го порядка.
Ну, для начала найти хотя бы тройку MODLS.
Для этого надо получить много наборов ОДЛК посолиднее и проверить их на ортогональные пары.
Самый солидный набор должен получиться от ДЛК, который я проверяла выше. Он имеет 24752 Д-трансверсалей и >>276464 ОДЛК.
Правда, я нашла ДЛК, у которого ещё больше Д-трансверсалей - 24901, но не проверяла его на ОДЛК. Этот ДЛК тоже показан выше.
Вот эти наборы ОДЛК будут очень большие. Я их найти не смогу на своём ПК.
А потом и проверка этих огромных наборов на ортогональные пары будет выполняться очень долго.
Понятно, что чем больше набор ОДЛК, тем дольше будет выполняться проверка на ортогональные пары.
Harry отмечает это

The speed degrades rapidly with file size.
The order 12 file that you sent with 41,644 squares took only 1 minute 12 seconds.
Another order 12 file with 442,696 squares took 2 hours 27 minutes.

Кстати, он проверил набор ОДЛК 12-го порядка, состоящий из 41644 ОДЛК.
Этот набор получен от ДЛК, построенного Черновым.
Ортогональных пар в этом наборе не найдено.
У Harry проверка этого набора заняла 1 мин. 12 сек.

PS. Вспомним историю. Паркер нашёл ЛК 10-го порядка, у которого более 12 миллионов ОЛК. Хороший набор!
Каково же было его огорчение, когда он не нашёл в этом наборе ни одной ортогональной пары ЛК! Тройка MOLS не была найдена.
Не найдена она до сих пор, насколько мне известно.
Если я уже пропустила это важное событие, сообщите, пожалуйста.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Далее проверила набор из 4 MODLS 15-го порядка, найденный мной

1 7 12 10 9 3 15 8 2 14 11 4 13 5 6
3 2 8 13 11 10 4 9 1 12 5 14 6 7 15
2 4 3 9 14 12 11 10 13 6 1 7 8 15 5
14 3 5 4 10 1 13 11 7 2 8 9 15 6 12
8 1 4 6 5 11 2 12 3 9 10 15 7 13 14
4 9 2 5 7 6 12 13 10 11 15 8 14 1 3
11 5 10 3 6 8 7 14 12 15 9 1 2 4 13
9 10 11 12 13 14 1 15 8 7 6 5 4 3 2
6 11 9 8 2 15 5 7 14 1 13 10 3 12 4
10 8 7 1 15 4 3 6 5 13 14 12 9 2 11
7 6 14 15 3 2 10 5 9 4 12 13 11 8 1
5 13 15 2 1 9 14 4 6 8 3 11 12 10 7
12 15 1 14 8 13 6 3 4 5 7 2 10 11 9
15 14 13 7 12 5 8 2 11 3 4 6 1 9 10
13 12 6 11 4 7 9 1 15 10 2 3 5 14 8

1 11 8 3 6 12 9 14 7 2 10 5 15 13 4
8 2 12 9 4 7 13 1 3 11 6 15 14 5 10
4 9 3 13 10 5 8 2 12 7 15 1 6 11 14
13 5 10 4 14 11 6 3 8 15 2 7 12 1 9
9 14 6 11 5 1 12 4 15 3 8 13 2 10 7
15 10 1 7 12 6 2 5 4 9 14 3 11 8 13
5 15 11 2 8 13 7 6 10 1 4 12 9 14 3
12 13 14 1 2 3 4 15 11 10 9 8 7 6 5
10 7 2 5 11 8 3 13 14 6 1 9 4 15 12
6 1 4 10 7 2 11 12 9 13 5 14 8 3 15
14 3 9 6 1 10 15 11 5 8 12 4 13 7 2
2 8 5 14 9 15 1 10 13 4 7 11 3 12 6
7 4 13 8 15 14 5 9 1 12 3 6 10 2 11
3 12 7 15 13 4 10 8 6 14 11 2 5 9 1
11 6 15 12 3 9 14 7 2 5 13 10 1 4 8
 
1 9 7 13 3 2 12 5 8 15 4 14 11 6 10
9 2 10 8 14 4 3 6 15 5 1 12 7 11 13
15 10 3 11 9 1 5 7 6 2 13 8 12 14 4
7 15 11 4 12 10 2 8 3 14 9 13 1 5 6
4 8 15 12 5 13 11 9 1 10 14 2 6 7 3
2 5 9 15 13 6 14 10 11 1 3 7 8 4 12
12 3 6 10 15 14 7 11 2 4 8 9 5 13 1
14 1 2 3 4 5 6 15 13 12 11 10 9 8 7
8 6 12 2 1 11 9 4 14 7 15 3 13 10 5
5 11 1 14 10 8 4 3 7 13 6 15 2 12 9
10 14 13 9 7 3 8 2 4 6 12 5 15 1 11
13 12 8 6 2 7 10 1 9 3 5 11 4 15 14
11 7 5 1 6 9 13 14 12 8 2 4 10 3 15
6 4 14 5 8 12 15 13 10 11 7 1 3 9 2
3 13 4 7 11 15 1 12 5 9 10 6 14 2 8

1 6 13 7 12 5 8 3 9 10 15 2 4 11 14
10 2 7 14 8 13 6 4 11 15 3 5 12 1 9
12 11 3 8 1 9 14 5 15 4 6 13 2 10 7
15 13 12 4 9 2 10 6 5 7 14 3 11 8 1
6 15 14 13 5 10 3 7 8 1 4 12 9 2 11
9 7 15 1 14 6 11 8 2 5 13 10 3 12 4
3 10 8 15 2 1 7 9 6 14 11 4 13 5 12
13 14 1 2 3 4 5 15 12 11 10 9 8 7 6
5 12 6 11 4 7 13 2 14 8 9 15 1 3 10
11 5 10 3 6 12 9 1 4 13 7 8 15 14 2
4 9 2 5 11 8 1 14 10 3 12 6 7 15 13
8 1 4 10 7 14 12 13 3 9 2 11 5 6 15
14 3 9 6 13 11 15 12 7 2 8 1 10 4 5
2 8 5 12 10 15 4 11 13 6 1 7 14 9 3
7 4 11 9 15 3 2 10 1 12 5 14 6 13 8

Протокол этой проверки

Order? 15

Enter the name of the squares file: inp
..output file inpPairs.txt
..output file inpPairNos.txt
squares 4 orthogonal pairs 6

Вывод программы

2:  1
3:  1 2
4:  1 2 3

Всё верно: в этом наборе 6 ортогональных пар.

Отличная программа!
Огромная благодарность Harry.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Согласно показанной выше теореме может существовать даже группа из 5 MODLS 12-го порядка.

Я отредактировала эту фразу (сначала она была другая).
Может существовать, но не обязательно существует.
Даже о тройке MODLS 12-го порядка эта теорема ничего не утверждает.

Посмотрев внимательно на перевод указанной теоремы

Существует пять попарно ортогональных диагональных латинских квадратов каждого
порядок n, где n>164. Порядок 2 ≤ n ≤ 7 невозможен; единственные заказы на которые
Существуют нерешенные вопросы:

10 12 14 15 18 20 21 22 24 26
28 30 33 34 35 36 38 39 40 42
44 45 46 48 50 51 52 54 55 60
62 66 68 69 70 74 76 82 84 90
98 106 164

поняла, что для порядка 12 существование 5 MODLS не установлено, как и для порядка 10.
Вот для порядков n>164 уже нет вопросов.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё один пример покажу проверки набора на ортогональные пары.
Это набор из 19139 ОДЛК, полученный от другого ДЛК из полной системы MOLS 11-го порядка.
Протокол этой проверки

Order? 11

Enter the name of the squares file: inp
..output file inpPairs.txt
..output file inpPairNos.txt
squares 19139 orthogonal pairs 186

elapsed time 0:01:24

Интересно: найдено тоже 186 ортогональных пар, как и для набора из 26914 ОДЛК.
Вывод программы

3095:  1987
3096:  1987
3097:  1987
3106:  1987
3107:  1987
3108:  1987
3110:  1987
3111:  1987
3112:  1987
3146:  1987
3147:  1987
3149:  1987
3152:  1987
3156:  1987
3158:  1987
4410:  1987
4414:  1987
4443:  1987
4922:  1987
4925:  1987
4929:  1987
4937:  1987
4938:  1987
4939:  1987
4945:  1987
4946:  1987
4947:  1987
4954:  1987
4955:  1987
4956:  1987
4972:  1987
4973:  1987
4975:  1987
6089:  1987
6122:  1987
6159:  1987 4414
7979:  1987
7980:  1987
7981:  1987
7989:  1987
7990:  1987
7991:  1987
7999:  1987
8000:  1987
8002:  1987
8029:  1987
8033:  1987
8035:  1987
8037:  1987
8039:  1987
8040:  1987
8617:  1987
8618:  1987
8619:  1987
8621:  1987
8622:  1987
8623:  1987
8631:  1987
8632:  1987
8633:  1987
8663:  1987
8667:  1987
8670:  1987
8674:  1987
8675:  1987
8676:  1987
9256:  1987
9257:  1987
9261:  1987
9265:  1987
9266:  1987
9267:  1987
9272:  1987
9273:  1987
9274:  1987
9279:  1987
9280:  1987
9281:  1987
9292:  1987
9293:  1987
9294:  1987
9338:  1987
9411:  1987
9444:  1987
9445:  1987
9447:  1987 4414 6159
9519:  1987
9584:  1987
9585:  1987
9586:  1987
9613:  1987
9614:  1987
9615:  1987
9626:  1987
9627:  1987
9632:  1987
9636:  1987
9637:  1987
9638:  1987
9646:  1987
9648:  1987
9649:  1987
10109:  1987
10112:  1987
10116:  1987
10134:  1987
10135:  1987
10137:  1987
10138:  1987
10139:  1987
10140:  1987
10141:  1987
10142:  1987
10143:  1987
10166:  1987
10167:  1987
10168:  1987
11598:  1987
11621:  1987
11626:  1987 4414 6159 9447
13370:  1987
13371:  1987
13373:  1987
13375:  1987
13376:  1987
13377:  1987
13381:  1987
13382:  1987
13383:  1987
13421:  1987
13424:  1987
13426:  1987
13430:  1987
13431:  1987
13432:  1987
14652:  1987
14666:  1987 4414 6159 9447 11626
14690:  1987
15202:  1987
15203:  1987
15205:  1987
15208:  1987
15210:  1987
15211:  1987
15218:  1987
15219:  1987
15220:  1987
15254:  1987
15256:  1987
15258:  1987
15268:  1987
15269:  1987
15270:  1987
17569:  1987
17570:  1987
17571:  1987
17587:  1987
17588:  1987
17589:  1987
17590:  1987
17591:  1987
17592:  1987
17596:  1987
17598:  1987
17600:  1987
17618:  1987
17619:  1987
17620:  1987
18433:  1987
18440:  1987
18447:  1987 4414 6159 9447 11626 14666

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Всё, наборы ОДЛК 12-го порядка у меня закончились.
Точнее, они есть, но... я их все канонизировала.
А проверять-то надо не КФ ОДЛК, а сами ОДЛК!
Придётся искать все наборы ОДЛК 12-го порядка снова. Дурная голова черепашке покоя не даёт :)
Ну, наборы у меня получались не очень солидные, кроме последнего (276464 ОДЛК). Вот этот жалко!
Искать его снова - это же более 41 часа непрерывной работы.
Лучше попробовать ДЛК с 24901 Д-трансверсалей.
Но опять же надо кучу времени на это, причём непрерывно, прерывать-то нельзя, потому что программа не продолжает поиск с прерванного места.
Хорошо хоть найденные решения при прерывании не теряются, записываются в файл.

В общем, задача очень интересная, но... мои ресурсы не позволяют её решать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Выложила на Яндекс.Диск программу Белышева ortogon_u
https://yadi.sk/d/rW8gHaJgwLh3DA

Записала в файл input.txt этот ДЛК 12-го порядка, он имеет 24901 Д-трансверсалей

0 8 1 B 5 9 3 A 2 7 6 4
5 7 0 A 4 8 2 9 1 6 B 3
2 A 3 7 1 B 5 6 4 9 8 0
4 6 5 9 3 7 1 8 0 B A 2
3 B 4 8 2 6 0 7 5 A 9 1
7 3 8 0 6 4 A 5 9 2 1 B
8 4 9 1 7 5 B 0 A 3 2 6
9 5 A 2 8 0 6 1 B 4 3 7
A 0 B 3 9 1 7 2 6 5 4 8
1 9 2 6 0 A 4 B 3 8 7 5
B 1 6 4 A 2 8 3 7 0 5 9
6 2 7 5 B 3 9 4 8 1 0 A

Программа запускается обычно. При запуске программа запросит порядок ДЛК.
Введите его.

Если есть желание и интерес, попробуйте поискать ОДЛК к этому ДЛК.
Конечно, тут можно найти только какую-то небольшую часть набора (за несколько суток непрерывной работы на одном ПК).
Чтобы решить задачу полностью, одного ПК явно недостаточно.

Вы можете искать по этой программе ОДЛК к любым ДЛК разных порядков.
Правда, для порядков, начиная с 15, программа чаще всего ругается :) и ничего не ищет (слишком много Д-трансверсалей в исходном ДЛК).

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот запустила программу с этим ДЛК

Проверка ДЛК12 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 24901
Соквадратов:     57
Время в сек:     25

1994 820 249 10 4 4

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg