ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 . . . 21 · 22 · 23 · 24 · 25 · 26 · 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила ассоциативные SODLS 28-го порядка. Да, они являются DSODLS. Далее в теме нет ни одной ортогональной пары ДЛК 30-го порядка, SODLS тоже нет. Сейчас попробую по программе Harry найти SODLS, заодно и ортогональная пара будет. Готово! Мгновенно построился 0 22 24 11 23 27 28 8 6 5 4 14 13 1 29 2 3 16 15 20 9 12 25 19 18 17 21 10 7 26 13 1 21 23 12 22 26 27 9 7 6 5 14 2 28 3 4 15 19 10 0 24 18 17 29 20 11 8 25 16 14 13 2 20 22 0 21 25 26 10 8 7 6 3 27 4 5 18 11 1 23 17 29 28 19 12 9 24 16 15 7 14 13 3 19 21 1 20 24 25 11 9 8 4 26 5 6 12 2 22 29 28 27 18 0 10 23 16 15 17 9 8 14 13 4 18 20 2 19 23 24 12 10 5 25 6 7 3 21 28 27 26 17 1 11 22 16 15 29 0 11 10 9 14 13 5 17 19 3 18 22 23 0 6 24 7 8 20 27 26 25 29 2 12 21 16 15 28 1 4 1 12 11 10 14 13 6 29 18 4 17 21 22 7 23 8 9 26 25 24 28 3 0 20 16 15 27 2 5 19 21 2 0 12 11 14 13 7 28 17 5 29 20 8 22 9 10 24 23 27 4 1 19 16 15 26 3 6 18 25 19 20 3 1 0 12 14 13 8 27 29 6 28 9 21 10 11 22 26 5 2 18 16 15 25 4 7 17 24 23 27 18 19 4 2 1 0 14 13 9 26 28 7 10 20 11 12 25 6 3 17 16 15 24 5 8 29 23 22 21 8 26 17 18 5 3 2 1 14 13 10 25 27 11 19 12 0 7 4 29 16 15 23 6 9 28 22 21 20 24 26 9 25 29 17 6 4 3 2 14 13 11 24 12 18 0 1 5 28 16 15 22 7 10 27 21 20 19 23 8 23 25 10 24 28 29 7 5 4 3 14 13 12 0 17 1 2 27 16 15 21 8 11 26 20 19 18 22 9 6 3 4 5 6 7 8 9 10 11 12 0 1 2 13 15 16 14 29 17 18 19 20 21 22 23 24 25 26 27 28 28 27 26 25 24 23 22 21 20 19 18 17 29 16 14 13 15 2 1 0 12 11 10 9 8 7 6 5 4 3 29 28 27 26 25 24 23 22 21 20 19 18 17 14 16 15 13 1 0 12 11 10 9 8 7 6 5 4 3 2 4 5 6 7 8 9 10 11 12 0 1 2 3 15 13 14 16 28 29 17 18 19 20 21 22 23 24 25 26 27 22 19 23 28 10 2 11 6 29 21 15 16 1 27 5 20 25 17 13 14 24 9 3 4 26 18 8 12 0 7 20 24 29 9 1 10 5 17 22 15 16 0 23 28 4 21 26 6 18 13 14 25 8 2 3 27 19 7 11 12 25 17 8 0 9 4 18 23 15 16 12 24 21 29 3 22 27 11 5 19 13 14 26 7 1 2 28 20 6 10 18 7 12 8 3 19 24 15 16 11 25 22 26 17 2 23 28 9 10 4 20 13 14 27 6 0 1 29 21 5 6 11 7 2 20 25 15 16 10 26 23 27 19 18 1 24 29 4 8 9 3 21 13 14 28 5 12 0 17 22 10 6 1 21 26 15 16 9 27 24 28 20 5 19 0 25 17 23 3 7 8 2 22 13 14 29 4 11 12 18 5 0 22 27 15 16 8 28 25 29 21 4 9 20 12 26 18 19 24 2 6 7 1 23 13 14 17 3 10 11 12 23 28 15 16 7 29 26 17 22 3 8 4 21 11 27 19 10 20 25 1 5 6 0 24 13 14 18 2 9 24 29 15 16 6 17 27 18 23 2 7 3 11 22 10 28 20 8 9 21 26 0 4 5 12 25 13 14 19 1 17 15 16 5 18 28 19 24 1 6 2 10 25 23 9 29 21 0 7 8 22 27 12 3 4 11 26 13 14 20 15 16 4 19 29 20 25 0 5 1 9 26 18 24 8 17 22 21 12 6 7 23 28 11 2 3 10 27 13 14 16 3 20 17 21 26 12 4 0 8 27 19 15 25 7 18 23 14 22 11 5 6 24 29 10 1 2 9 28 13 2 21 18 22 27 11 3 12 7 28 20 15 16 26 6 19 24 13 14 23 10 4 5 25 17 9 0 1 8 29 DSODLS не является. Порядок 30 принадлежит серии порядков n=4k+2, поэтому ассоциативных ДЛК данного порядка не существует. Так, ещё одно белое пятно ликвидировали. До порядка 30 теперь есть и ортогональные пары, и SODLS. На DSODLS тоже все ДЛК, являющиеся SODLS, проверены. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Последовательность OEIS https://oeis.org/A287648 утверждена. A287648 Maximum number of diagonal transversals in a diagonal Latin square of order n. Добавленные мной оценки a(11) >= 4828, a(12) >= 24901, a(13) >= 131106, a(14) >= 364596, a(15) >= 389318 Вот здесь https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6211 я показала квадратик 8-го порядка [DLK(128):1021] 0 5 4 2 3 6 7 1 4 1 3 5 7 2 0 6 6 0 2 7 5 3 1 4 1 7 6 3 2 4 5 0 7 3 1 6 4 0 2 5 2 6 7 0 1 5 4 3 3 4 5 1 0 7 6 2 5 2 0 4 6 1 3 7 Он имеет 120 диагональных трансверсалей. Вывод программы Белышева ortogon_u Проверка ДЛК8 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 120 Соквадратов: 128 Время в сек: 5 Это член последовательности a(8)=120. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу представителей для остальных членов последовательности. a(4)=4 0 1 2 3 2 3 0 1 3 2 1 0 1 0 3 2 Вывод программы Белышева Проверка ДЛК4 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 4 Соквадратов: 1 a(5)=5 0 1 2 3 4 2 3 4 0 1 4 0 1 2 3 1 2 3 4 0 3 4 0 1 2 Проверка ДЛК5 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 5 Соквадратов: 1 a(7)=27 0 1 2 3 4 5 6 2 3 4 5 6 0 1 4 5 6 0 1 2 3 6 0 1 2 3 4 5 1 2 3 4 5 6 0 3 4 5 6 0 1 2 5 6 0 1 2 3 4 Проверка ДЛК7 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 27 Соквадратов: 3 Все эти ДЛК я взяла из полной системы MOLS соотсветствующего порядка. a(6)=6 пока отсутствует. Интересно, для этого порядка программа Белышева будет считать Д-трансверсали? Или поругается? ОДЛК для данного порядка не существует. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нашла ДЛК 6-го порядка в своей статье Построение диагональных латинских квадратов 0 1 2 3 4 5 4 2 5 0 3 1 3 0 4 1 5 2 1 3 0 5 2 4 5 4 3 2 1 0 2 5 1 4 0 3 Программа Белышева не ругалась, Д-трансверсали посчитала Проверка ДЛК6 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 6 Соквадратов: 0 Теперь все представители показаны. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это ДЛК 16-го порядка, построенный методом Гергели 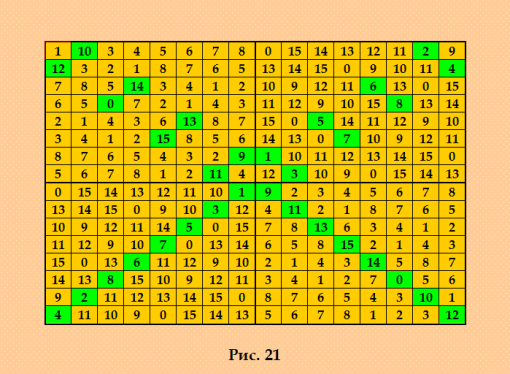 Смотрите статью по ссылке в предыдущем посте. Хороший квадратик! Я попросила Harry White посчитать Д-трансверсали в этом ДЛК. Программа Белышева не считает в этом ДЛК Д-трансверсали, просто сообщает, что их количество превышает максимальное значение, установленное в программе. Harry White сообщил, что в этом ДЛК 15456144 диагональных трансверсали. Это пока единственное известное мне значение количества Д-трансверсалей для ДЛК 16-го порядка. Вполне возможно, что оно не максимальное. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Этот ДЛК 16-го порядка показал Tomas Brada 0 14 1 7 2 4 3 5 13 11 12 10 15 9 6 8 15 1 6 0 5 3 4 2 10 12 11 13 8 14 9 7 3 5 2 12 1 7 0 6 14 8 15 9 4 10 13 11 4 2 13 3 6 0 7 1 9 15 8 14 11 5 10 12 6 0 7 1 4 10 5 3 11 13 2 12 9 15 8 14 1 7 0 6 11 5 2 4 12 10 13 3 14 8 15 9 5 3 4 2 7 1 6 8 0 14 9 15 10 12 11 13 2 4 3 5 0 6 9 7 15 1 14 8 13 11 12 10 13 11 12 10 15 9 14 0 8 6 1 7 2 4 3 5 10 12 11 13 8 14 1 15 7 9 6 0 5 3 4 2 14 8 15 9 12 2 13 11 3 5 10 4 1 7 0 6 9 15 8 14 3 13 10 12 4 2 5 11 6 0 7 1 11 13 10 4 9 15 8 14 6 0 7 1 12 2 5 3 12 10 5 11 14 8 15 9 1 7 0 6 3 13 2 4 8 6 9 15 10 12 11 13 5 3 4 2 7 1 14 0 7 9 14 8 13 11 12 10 2 4 3 5 0 6 1 15 init_trans(16) used 851 nodes num_trans: 15456144 time: 10.5s отсюда https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5909 У этого ДЛК такое же количество Д-трансверсалей. Возможно, эти ДЛК изоморфны. Проверить нечем, канонизатора для ДЛК 16-го порядка у меня нет. По структуре этот ДЛК очень похож на ДЛК, построенный методом Гергели. Оба ДЛК симметричные по Гергели/Брауну и оба "брауны". My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Изменилась ссылка на программу Harry White для подсчёта трансверсалей в ЛК/ДЛК http://budshaw.ca/Download.html#transversals My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Далее в теме нет ни одной ортогональной пары ДЛК 30-го порядка, SODLS тоже нет. Оказывается, ортогональная пара ДЛК 30-го порядка есть в теме, смотрите тут https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5798 Ортогональная пара построена методом Пелегрино-Ланселотти по программе А. Чернова. Ну, теперь есть две ортогональные пары. Ортогональной пары ДЛК 33-го порядка пока не вижу. Сейчас посмотрю внимательнее. Не нашла. И для ДЛК 34 порядка тоже не нашла ортогональную пару. Сейчас попробую через SODLS с помощью программы Harry White. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
SODLS 33-го порядка готов 0 6 7 4 1 2 16 5 17 20 24 21 22 23 19 18 3 25 28 32 29 30 31 27 26 8 11 15 12 13 14 10 9 7 1 4 2 5 16 3 6 19 18 22 23 24 21 17 20 0 27 26 30 31 32 29 25 28 10 9 13 14 15 12 8 11 4 5 2 16 6 3 0 1 22 23 19 18 17 20 24 21 7 30 31 27 26 25 28 32 29 13 14 10 9 8 11 15 12 2 16 6 3 0 1 7 4 24 21 17 20 19 18 22 23 5 32 29 25 28 27 26 30 31 15 12 8 11 10 9 13 14 6 0 3 1 4 7 5 16 18 19 23 22 21 24 20 17 2 26 27 31 30 29 32 28 25 9 10 14 13 12 15 11 8 3 4 1 7 16 5 2 0 20 17 21 24 23 22 18 19 6 28 25 29 32 31 30 26 27 11 8 12 15 14 13 9 10 1 7 16 5 2 0 6 3 21 24 20 17 18 19 23 22 4 29 32 28 25 26 27 31 30 12 15 11 8 9 10 14 13 16 2 5 0 3 6 4 7 23 22 18 19 20 17 21 24 1 31 30 26 27 28 25 29 32 14 13 9 10 11 8 12 15 25 28 32 29 30 31 27 26 8 14 15 12 9 10 16 13 11 0 3 7 4 5 6 2 1 17 20 24 21 22 23 19 18 27 26 30 31 32 29 25 28 15 9 12 10 13 16 11 14 8 2 1 5 6 7 4 0 3 19 18 22 23 24 21 17 20 30 31 27 26 25 28 32 29 12 13 10 16 14 11 8 9 15 5 6 2 1 0 3 7 4 22 23 19 18 17 20 24 21 32 29 25 28 27 26 30 31 10 16 14 11 8 9 15 12 13 7 4 0 3 2 1 5 6 24 21 17 20 19 18 22 23 26 27 31 30 29 32 28 25 14 8 11 9 12 15 13 16 10 1 2 6 5 4 7 3 0 18 19 23 22 21 24 20 17 28 25 29 32 31 30 26 27 11 12 9 15 16 13 10 8 14 3 0 4 7 6 5 1 2 20 17 21 24 23 22 18 19 29 32 28 25 26 27 31 30 9 15 16 13 10 8 14 11 12 4 7 3 0 1 2 6 5 21 24 20 17 18 19 23 22 31 30 26 27 28 25 29 32 16 10 13 8 11 14 12 15 9 6 5 1 2 3 0 4 7 23 22 18 19 20 17 21 24 5 3 0 6 7 4 1 2 13 11 8 14 15 12 9 10 16 22 20 17 23 24 21 18 19 30 28 25 31 32 29 26 27 8 11 15 12 13 14 10 9 25 28 32 29 30 31 27 26 20 17 23 24 21 18 19 16 22 0 3 7 4 5 6 2 1 10 9 13 14 15 12 8 11 27 26 30 31 32 29 25 28 17 24 18 21 19 22 16 20 23 2 1 5 6 7 4 0 3 13 14 10 9 8 11 15 12 30 31 27 26 25 28 32 29 24 21 22 19 16 23 20 17 18 5 6 2 1 0 3 7 4 15 12 8 11 10 9 13 14 32 29 25 28 27 26 30 31 22 19 16 23 20 17 18 24 21 7 4 0 3 2 1 5 6 9 10 14 13 12 15 11 8 26 27 31 30 29 32 28 25 19 23 17 20 18 21 24 22 16 1 2 6 5 4 7 3 0 11 8 12 15 14 13 9 10 28 25 29 32 31 30 26 27 23 20 21 18 24 16 22 19 17 3 0 4 7 6 5 1 2 12 15 11 8 9 10 14 13 29 32 28 25 26 27 31 30 21 18 24 16 22 19 17 23 20 4 7 3 0 1 2 6 5 14 13 9 10 11 8 12 15 31 30 26 27 28 25 29 32 18 16 19 22 17 20 23 21 24 6 5 1 2 3 0 4 7 17 20 24 21 22 23 19 18 0 3 7 4 5 6 2 1 28 8 11 15 12 13 14 10 9 25 31 32 29 26 27 16 30 19 18 22 23 24 21 17 20 2 1 5 6 7 4 0 3 25 10 9 13 14 15 12 8 11 32 26 29 27 30 16 28 31 22 23 19 18 17 20 24 21 5 6 2 1 0 3 7 4 32 13 14 10 9 8 11 15 12 29 30 27 16 31 28 25 26 24 21 17 20 19 18 22 23 7 4 0 3 2 1 5 6 30 15 12 8 11 10 9 13 14 27 16 31 28 25 26 32 29 18 19 23 22 21 24 20 17 1 2 6 5 4 7 3 0 27 9 10 14 13 12 15 11 8 31 25 28 26 29 32 30 16 20 17 21 24 23 22 18 19 3 0 4 7 6 5 1 2 31 11 8 12 15 14 13 9 10 28 29 26 32 16 30 27 25 21 24 20 17 18 19 23 22 4 7 3 0 1 2 6 5 29 12 15 11 8 9 10 14 13 26 32 16 30 27 25 31 28 23 22 18 19 20 17 21 24 6 5 1 2 3 0 4 7 26 14 13 9 10 11 8 12 15 16 27 30 25 28 31 29 32 Ну вот есть ортогональная пара теперь для данного порядка. DSODLS данный ДЛК не является, он не ассоциативный. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И SODLS 34-го порядка тоже готов 33 31 18 26 32 30 21 27 7 5 2 0 6 4 3 1 29 28 25 23 20 16 24 22 17 19 15 13 10 8 14 12 11 9 18 32 27 29 21 33 26 28 4 6 1 3 5 7 0 2 31 30 22 24 19 17 23 25 16 20 12 14 9 11 13 15 8 10 26 28 31 18 27 29 30 21 0 2 5 7 1 3 4 6 32 33 16 20 23 25 19 17 22 24 8 10 13 15 9 11 12 14 29 18 32 30 28 21 33 31 3 1 6 4 2 0 7 5 26 27 17 19 24 22 20 16 25 23 11 9 14 12 10 8 15 13 28 26 21 31 29 27 18 30 2 0 7 5 3 1 6 4 33 32 20 16 25 23 17 19 24 22 10 8 15 13 11 9 14 12 21 29 30 32 18 28 31 33 1 3 4 6 0 2 5 7 27 26 19 17 22 24 16 20 23 25 9 11 12 14 8 10 13 15 31 33 26 21 30 32 27 18 5 7 0 2 4 6 1 3 28 29 23 25 16 20 22 24 19 17 13 15 8 10 12 14 9 11 32 21 29 27 33 18 28 26 6 4 3 1 7 5 2 0 30 31 24 22 17 19 25 23 20 16 14 12 11 9 15 13 10 8 15 13 10 8 14 12 11 9 25 19 22 20 17 18 21 16 24 23 7 5 2 0 6 4 3 1 33 31 28 26 32 30 29 27 12 14 9 11 13 15 8 10 21 24 16 23 20 25 17 22 19 18 4 6 1 3 5 7 0 2 30 32 27 29 31 33 26 28 8 10 13 15 9 11 12 14 20 17 23 16 18 24 25 21 22 19 0 2 5 7 1 3 4 6 26 28 31 33 27 29 30 32 11 9 14 12 10 8 15 13 18 25 24 22 19 17 16 23 21 20 3 1 6 4 2 0 7 5 29 27 32 30 28 26 33 31 10 8 15 13 11 9 14 12 23 16 19 17 21 22 18 20 25 24 2 0 7 5 3 1 6 4 28 26 33 31 29 27 32 30 9 11 12 14 8 10 13 15 17 18 21 24 25 20 23 19 16 22 1 3 4 6 0 2 5 7 27 29 30 32 26 28 31 33 13 15 8 10 12 14 9 11 16 22 20 18 24 21 19 25 23 17 5 7 0 2 4 6 1 3 31 33 26 28 30 32 27 29 14 12 11 9 15 13 10 8 22 21 17 19 23 16 24 18 20 25 6 4 3 1 7 5 2 0 32 30 29 27 33 31 28 26 27 30 33 28 31 26 29 32 19 20 18 25 16 23 22 24 17 21 9 12 15 10 13 8 11 14 1 4 7 2 5 0 3 6 30 27 28 33 26 31 32 29 24 23 25 21 22 19 20 17 18 16 12 9 10 15 8 13 14 11 4 1 2 7 0 5 6 3 7 5 2 0 6 4 3 1 33 31 28 26 32 30 29 27 11 10 15 13 18 8 14 12 21 9 25 23 20 16 24 22 17 19 4 6 1 3 5 7 0 2 30 32 27 29 31 33 26 28 13 12 18 14 9 11 21 15 8 10 22 24 19 17 23 25 16 20 0 2 5 7 1 3 4 6 26 28 31 33 27 29 30 32 14 15 8 10 13 18 9 11 12 21 16 20 23 25 19 17 22 24 3 1 6 4 2 0 7 5 29 27 32 30 28 26 33 31 8 9 11 18 14 12 10 21 15 13 17 19 24 22 20 16 25 23 2 0 7 5 3 1 6 4 28 26 33 31 29 27 32 30 15 14 10 8 21 13 11 9 18 12 20 16 25 23 17 19 24 22 1 3 4 6 0 2 5 7 27 29 30 32 26 28 31 33 9 8 21 11 12 14 18 10 13 15 19 17 22 24 16 20 23 25 5 7 0 2 4 6 1 3 31 33 26 28 30 32 27 29 10 11 13 15 8 21 12 14 9 18 23 25 16 20 22 24 19 17 6 4 3 1 7 5 2 0 32 30 29 27 33 31 28 26 12 13 14 21 11 9 15 18 10 8 24 22 17 19 25 23 20 16 25 23 20 16 24 22 17 19 15 13 10 8 14 12 11 9 3 2 33 31 28 26 32 30 29 27 7 5 18 0 6 4 21 1 22 24 19 17 23 25 16 20 12 14 9 11 13 15 8 10 5 4 30 32 27 29 31 33 26 28 18 6 1 3 21 7 0 2 16 20 23 25 19 17 22 24 8 10 13 15 9 11 12 14 6 7 26 28 31 33 27 29 30 32 0 2 5 18 1 3 4 21 17 19 24 22 20 16 25 23 11 9 14 12 10 8 15 13 0 1 29 27 32 30 28 26 33 31 3 18 6 4 2 21 7 5 20 16 25 23 17 19 24 22 10 8 15 13 11 9 14 12 7 6 28 26 33 31 29 27 32 30 2 0 21 5 3 1 18 4 19 17 22 24 16 20 23 25 9 11 12 14 8 10 13 15 1 0 27 29 30 32 26 28 31 33 21 3 4 6 18 2 5 7 23 25 16 20 22 24 19 17 13 15 8 10 12 14 9 11 2 3 31 33 26 28 30 32 27 29 5 7 0 21 4 6 1 18 24 22 17 19 25 23 20 16 14 12 11 9 15 13 10 8 4 5 32 30 29 27 33 31 28 26 6 21 3 1 7 18 2 0 Порядок 34 принадлежит серии порядков n=4k+2, поэтому ассоциативных ДЛК данного порядка не существует. Найденный SODLS не является DSODLS. Теперь имеем и ортогональную пару ДЛК 34-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Напомню проблемные порядки до n=50, которые у нас пока без ортогональных пар ДЛК: 21, 33, 38, 39 и 46. отсюда https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5819 Для порядков 21 и 33 уже найдены ортогональные пары с помощью SODLS. Сейчас попробую найти SODLS для порядков 38, 39 и 46. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это SODLS 38-го порядка, построился мгновенно 0 6 5 4 19 20 14 31 37 36 35 34 33 32 24 30 29 28 27 26 25 3 2 1 21 22 23 18 17 16 15 7 13 12 11 10 9 8 14 1 0 6 5 19 20 33 32 31 37 36 35 34 26 25 24 30 29 28 27 4 3 2 16 15 21 22 23 18 17 9 8 7 13 12 11 10 20 14 2 1 0 6 19 35 34 33 32 31 37 36 28 27 26 25 24 30 29 5 4 3 18 17 16 15 21 22 23 11 10 9 8 7 13 12 19 20 14 3 2 1 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 6 5 4 22 23 18 17 16 15 21 13 12 11 10 9 8 7 1 19 20 14 4 3 2 32 31 37 36 35 34 33 25 24 30 29 28 27 26 0 6 5 15 21 22 23 18 17 16 8 7 13 12 11 10 9 3 2 19 20 14 5 4 34 33 32 31 37 36 35 27 26 25 24 30 29 28 1 0 6 17 16 15 21 22 23 18 10 9 8 7 13 12 11 5 4 3 19 20 14 6 36 35 34 33 32 31 37 29 28 27 26 25 24 30 2 1 0 23 18 17 16 15 21 22 12 11 10 9 8 7 13 21 22 23 18 17 16 15 7 13 12 11 19 20 14 0 6 5 4 3 2 1 10 9 8 31 37 36 35 34 33 32 24 30 29 28 27 26 25 16 15 21 22 23 18 17 14 8 7 13 12 19 20 2 1 0 6 5 4 3 11 10 9 33 32 31 37 36 35 34 26 25 24 30 29 28 27 18 17 16 15 21 22 23 20 14 9 8 7 13 19 4 3 2 1 0 6 5 12 11 10 35 34 33 32 31 37 36 28 27 26 25 24 30 29 22 23 18 17 16 15 21 19 20 14 10 9 8 7 6 5 4 3 2 1 0 13 12 11 37 36 35 34 33 32 31 30 29 28 27 26 25 24 15 21 22 23 18 17 16 8 19 20 14 11 10 9 1 0 6 5 4 3 2 7 13 12 32 31 37 36 35 34 33 25 24 30 29 28 27 26 17 16 15 21 22 23 18 10 9 19 20 14 12 11 3 2 1 0 6 5 4 8 7 13 34 33 32 31 37 36 35 27 26 25 24 30 29 28 23 18 17 16 15 21 22 12 11 10 19 20 14 13 5 4 3 2 1 0 6 9 8 7 36 35 34 33 32 31 37 29 28 27 26 25 24 30 31 37 36 35 34 33 32 24 30 29 28 27 26 25 14 19 23 15 20 22 18 17 16 21 7 13 12 11 10 9 8 0 6 5 4 3 2 1 33 32 31 37 36 35 34 26 25 24 30 29 28 27 16 15 18 21 14 23 19 20 17 22 9 8 7 13 12 11 10 2 1 0 6 5 4 3 35 34 33 32 31 37 36 28 27 26 25 24 30 29 15 22 16 23 17 18 21 19 20 14 11 10 9 8 7 13 12 4 3 2 1 0 6 5 37 36 35 34 33 32 31 30 29 28 27 26 25 24 18 20 22 17 21 16 14 23 15 19 13 12 11 10 9 8 7 6 5 4 3 2 1 0 32 31 37 36 35 34 33 25 24 30 29 28 27 26 17 21 14 19 18 20 15 22 23 16 8 7 13 12 11 10 9 1 0 6 5 4 3 2 34 33 32 31 37 36 35 27 26 25 24 30 29 28 20 14 21 22 23 19 17 16 18 15 10 9 8 7 13 12 11 3 2 1 0 6 5 4 36 35 34 33 32 31 37 29 28 27 26 25 24 30 19 23 17 16 22 15 20 14 21 18 12 11 10 9 8 7 13 5 4 3 2 1 0 6 6 0 1 2 3 4 5 13 7 8 9 10 11 12 23 16 15 18 19 17 22 21 14 20 30 24 25 26 27 28 29 37 31 32 33 34 35 36 4 5 6 0 1 2 3 11 12 13 7 8 9 10 21 18 19 20 16 14 23 15 22 17 28 29 30 24 25 26 27 35 36 37 31 32 33 34 2 3 4 5 6 0 1 9 10 11 12 13 7 8 22 17 20 14 15 21 16 18 19 23 26 27 28 29 30 24 25 33 34 35 36 37 31 32 7 13 12 11 10 9 8 0 6 5 4 3 2 1 31 37 36 35 34 33 32 27 26 25 24 30 29 28 19 20 14 21 22 23 18 17 16 15 9 8 7 13 12 11 10 2 1 0 6 5 4 3 33 32 31 37 36 35 34 28 27 26 14 25 24 30 29 19 20 16 15 21 22 23 18 17 11 10 9 8 7 13 12 4 3 2 1 0 6 5 35 34 33 32 31 37 36 29 28 27 20 14 26 25 24 30 19 18 17 16 15 21 22 23 13 12 11 10 9 8 7 6 5 4 3 2 1 0 37 36 35 34 33 32 31 30 29 28 19 20 14 27 26 25 24 22 23 18 17 16 15 21 8 7 13 12 11 10 9 1 0 6 5 4 3 2 32 31 37 36 35 34 33 24 30 29 25 19 20 14 28 27 26 15 21 22 23 18 17 16 10 9 8 7 13 12 11 3 2 1 0 6 5 4 34 33 32 31 37 36 35 25 24 30 27 26 19 20 14 29 28 17 16 15 21 22 23 18 12 11 10 9 8 7 13 5 4 3 2 1 0 6 36 35 34 33 32 31 37 26 25 24 29 28 27 19 20 14 30 23 18 17 16 15 21 22 24 30 29 28 27 26 25 21 22 23 18 17 16 15 7 13 12 11 10 9 8 34 33 32 0 6 5 4 3 2 1 31 37 36 35 19 20 14 26 25 24 30 29 28 27 16 15 21 22 23 18 17 9 8 7 13 12 11 10 35 34 33 2 1 0 6 5 4 3 14 32 31 37 36 19 20 28 27 26 25 24 30 29 18 17 16 15 21 22 23 11 10 9 8 7 13 12 36 35 34 4 3 2 1 0 6 5 20 14 33 32 31 37 19 30 29 28 27 26 25 24 22 23 18 17 16 15 21 13 12 11 10 9 8 7 37 36 35 6 5 4 3 2 1 0 19 20 14 34 33 32 31 25 24 30 29 28 27 26 15 21 22 23 18 17 16 8 7 13 12 11 10 9 31 37 36 1 0 6 5 4 3 2 32 19 20 14 35 34 33 27 26 25 24 30 29 28 17 16 15 21 22 23 18 10 9 8 7 13 12 11 32 31 37 3 2 1 0 6 5 4 34 33 19 20 14 36 35 29 28 27 26 25 24 30 23 18 17 16 15 21 22 12 11 10 9 8 7 13 33 32 31 5 4 3 2 1 0 6 36 35 34 19 20 14 37 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это SODLS 39-го порядка, построился мгновенно 0 4 3 2 1 34 38 37 21 20 29 33 32 31 30 35 36 24 28 27 26 25 16 17 15 19 18 23 22 10 14 13 12 11 5 9 8 7 6 2 1 0 4 3 20 35 34 38 21 31 30 29 33 32 36 37 26 25 24 28 27 17 18 22 16 15 19 23 12 11 10 14 13 7 6 5 9 8 4 3 2 1 0 21 20 36 35 34 33 32 31 30 29 37 38 28 27 26 25 24 18 19 23 22 17 16 15 14 13 12 11 10 9 8 7 6 5 1 0 4 3 2 35 21 20 37 36 30 29 33 32 31 38 34 25 24 28 27 26 19 15 16 23 22 18 17 11 10 14 13 12 6 5 9 8 7 3 2 1 0 4 37 36 21 20 38 32 31 30 29 33 34 35 27 26 25 24 28 15 16 18 17 23 22 19 13 12 11 10 14 8 7 6 5 9 10 14 13 21 20 5 9 8 7 6 0 4 3 2 1 11 12 34 38 37 23 22 35 36 29 33 32 31 30 24 28 27 26 25 15 19 18 17 16 20 11 10 14 21 7 6 5 9 8 2 1 0 4 3 12 13 22 35 34 38 23 36 37 31 30 29 33 32 26 25 24 28 27 17 16 15 19 18 21 20 12 11 10 9 8 7 6 5 4 3 2 1 0 13 14 23 22 36 35 34 37 38 33 32 31 30 29 28 27 26 25 24 19 18 17 16 15 11 21 20 13 12 6 5 9 8 7 1 0 4 3 2 14 10 35 23 22 37 36 38 34 30 29 33 32 31 25 24 28 27 26 16 15 19 18 17 13 12 21 20 14 8 7 6 5 9 3 2 1 0 4 10 11 37 36 23 22 38 34 35 32 31 30 29 33 27 26 25 24 28 18 17 16 15 19 24 28 27 26 25 15 19 18 17 16 10 14 13 23 22 30 31 5 9 8 7 6 11 12 0 4 3 2 1 34 38 37 36 35 29 33 32 21 20 26 25 24 28 27 17 16 15 19 18 22 11 10 14 23 31 32 7 6 5 9 8 12 13 2 1 0 4 3 36 35 34 38 37 20 30 29 33 21 28 27 26 25 24 19 18 17 16 15 23 22 12 11 10 32 33 9 8 7 6 5 13 14 4 3 2 1 0 38 37 36 35 34 21 20 31 30 29 25 24 28 27 26 16 15 19 18 17 11 23 22 13 12 33 29 6 5 9 8 7 14 10 1 0 4 3 2 35 34 38 37 36 30 21 20 32 31 27 26 25 24 28 18 17 16 15 19 13 12 23 22 14 29 30 8 7 6 5 9 10 11 3 2 1 0 4 37 36 35 34 38 32 31 21 20 33 12 13 14 10 11 36 37 38 34 35 17 18 19 15 16 20 22 2 3 4 0 1 23 21 26 27 28 24 25 7 8 9 5 6 31 32 33 29 30 14 10 11 12 13 38 34 35 36 37 19 15 16 17 18 23 21 4 0 1 2 3 20 22 28 24 25 26 27 9 5 6 7 8 33 29 30 31 32 34 38 37 36 35 29 33 32 23 22 24 28 27 26 25 6 7 15 19 18 17 16 30 31 10 14 13 12 11 5 9 8 21 20 0 4 3 2 1 36 35 34 38 37 22 30 29 33 23 26 25 24 28 27 7 8 17 16 15 19 18 31 32 12 11 10 14 13 20 6 5 9 21 2 1 0 4 3 38 37 36 35 34 23 22 31 30 29 28 27 26 25 24 8 9 19 18 17 16 15 32 33 14 13 12 11 10 21 20 7 6 5 4 3 2 1 0 35 34 38 37 36 30 23 22 32 31 25 24 28 27 26 9 5 16 15 19 18 17 33 29 11 10 14 13 12 6 21 20 8 7 1 0 4 3 2 37 36 35 34 38 32 31 23 22 33 27 26 25 24 28 5 6 18 17 16 15 19 29 30 13 12 11 10 14 8 7 21 20 9 3 2 1 0 4 7 8 9 5 6 31 32 33 29 30 12 13 14 10 11 21 23 36 37 38 34 35 22 20 17 18 19 15 16 2 3 4 0 1 26 27 28 24 25 9 5 6 7 8 33 29 30 31 32 14 10 11 12 13 22 20 38 34 35 36 37 21 23 19 15 16 17 18 4 0 1 2 3 28 24 25 26 27 5 9 8 23 22 0 4 3 2 1 34 38 37 36 35 25 26 29 33 32 31 30 6 7 24 28 27 21 20 15 19 18 17 16 10 14 13 12 11 22 6 5 9 23 2 1 0 4 3 36 35 34 38 37 26 27 31 30 29 33 32 7 8 20 25 24 28 21 17 16 15 19 18 12 11 10 14 13 23 22 7 6 5 4 3 2 1 0 38 37 36 35 34 27 28 33 32 31 30 29 8 9 21 20 26 25 24 19 18 17 16 15 14 13 12 11 10 6 23 22 8 7 1 0 4 3 2 35 34 38 37 36 28 24 30 29 33 32 31 9 5 25 21 20 27 26 16 15 19 18 17 11 10 14 13 12 8 7 23 22 9 3 2 1 0 4 37 36 35 34 38 24 25 32 31 30 29 33 5 6 27 26 21 20 28 18 17 16 15 19 13 12 11 10 14 15 19 18 17 16 10 14 13 12 11 5 9 8 7 6 1 2 0 4 3 21 20 25 26 34 38 37 36 35 29 33 32 31 30 24 28 27 23 22 17 16 15 19 18 12 11 10 14 13 7 6 5 9 8 2 3 20 1 0 4 21 26 27 36 35 34 38 37 31 30 29 33 32 22 25 24 28 23 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 3 4 21 20 2 1 0 27 28 38 37 36 35 34 33 32 31 30 29 23 22 26 25 24 16 15 19 18 17 11 10 14 13 12 6 5 9 8 7 4 0 1 21 20 3 2 28 24 35 34 38 37 36 30 29 33 32 31 25 23 22 27 26 18 17 16 15 19 13 12 11 10 14 8 7 6 5 9 0 1 3 2 21 20 4 24 25 37 36 35 34 38 32 31 30 29 33 27 26 23 22 28 29 33 32 31 30 24 28 27 26 25 15 19 18 21 20 16 17 10 14 13 12 11 1 2 5 9 8 7 6 0 4 3 23 22 34 38 37 36 35 31 30 29 33 32 26 25 24 28 27 20 16 15 19 21 17 18 12 11 10 14 13 2 3 7 6 5 9 8 22 1 0 4 23 36 35 34 38 37 33 32 31 30 29 28 27 26 25 24 21 20 17 16 15 18 19 14 13 12 11 10 3 4 9 8 7 6 5 23 22 2 1 0 38 37 36 35 34 30 29 33 32 31 25 24 28 27 26 16 21 20 18 17 19 15 11 10 14 13 12 4 0 6 5 9 8 7 1 23 22 3 2 35 34 38 37 36 32 31 30 29 33 27 26 25 24 28 18 17 21 20 19 15 16 13 12 11 10 14 0 1 8 7 6 5 9 3 2 23 22 4 37 36 35 34 38 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это SODLS 46-го порядка, построился мгновенно 0 5 27 1 6 8 4 3 2 37 43 44 41 38 39 45 42 40 28 34 35 32 29 30 36 33 31 7 18 24 25 22 19 20 26 23 21 9 15 16 13 10 11 17 14 12 2 1 4 7 0 27 5 6 3 44 38 41 39 42 45 40 43 37 35 29 32 30 33 36 31 34 28 8 25 19 22 20 23 26 21 24 18 16 10 13 11 14 17 12 15 9 1 8 2 27 3 4 7 5 6 41 42 39 45 43 40 37 38 44 32 33 30 36 34 31 28 29 35 0 22 23 20 26 24 21 18 19 25 13 14 11 17 15 12 9 10 16 4 6 8 3 7 2 0 27 1 39 45 43 40 37 38 44 41 42 30 36 34 31 28 29 35 32 33 5 20 26 24 21 18 19 25 22 23 11 17 15 12 9 10 16 13 14 3 7 0 5 4 6 1 8 27 43 37 40 38 41 44 42 45 39 34 28 31 29 32 35 33 36 30 2 24 18 21 19 22 25 23 26 20 15 9 12 10 13 16 14 17 11 6 0 7 8 27 5 3 2 4 40 41 38 44 45 42 39 37 43 31 32 29 35 36 33 30 28 34 1 21 22 19 25 26 23 20 18 24 12 13 10 16 17 14 11 9 15 5 27 3 2 8 1 6 0 7 38 44 45 42 39 37 43 40 41 29 35 36 33 30 28 34 31 32 4 19 25 26 23 20 18 24 21 22 10 16 17 14 11 9 15 12 13 27 2 1 4 5 3 8 7 0 45 39 42 37 40 43 41 44 38 36 30 33 28 31 34 32 35 29 6 26 20 23 18 21 24 22 25 19 17 11 14 9 12 15 13 16 10 7 4 5 6 2 0 27 1 8 42 40 37 43 44 41 38 39 45 33 31 28 34 35 32 29 30 36 3 23 21 18 24 25 22 19 20 26 14 12 9 15 16 13 10 11 17 18 24 25 22 19 20 26 23 21 9 14 27 10 15 17 13 12 11 0 6 7 4 1 2 8 5 3 16 37 43 44 41 38 39 45 42 40 28 34 35 32 29 30 36 33 31 25 19 22 20 23 26 21 24 18 11 10 13 16 9 27 14 15 12 7 1 4 2 5 8 3 6 0 17 44 38 41 39 42 45 40 43 37 35 29 32 30 33 36 31 34 28 22 23 20 26 24 21 18 19 25 10 17 11 27 12 13 16 14 15 4 5 2 8 6 3 0 1 7 9 41 42 39 45 43 40 37 38 44 32 33 30 36 34 31 28 29 35 20 26 24 21 18 19 25 22 23 13 15 17 12 16 11 9 27 10 2 8 6 3 0 1 7 4 5 14 39 45 43 40 37 38 44 41 42 30 36 34 31 28 29 35 32 33 24 18 21 19 22 25 23 26 20 12 16 9 14 13 15 10 17 27 6 0 3 1 4 7 5 8 2 11 43 37 40 38 41 44 42 45 39 34 28 31 29 32 35 33 36 30 21 22 19 25 26 23 20 18 24 15 9 16 17 27 14 12 11 13 3 4 1 7 8 5 2 0 6 10 40 41 38 44 45 42 39 37 43 31 32 29 35 36 33 30 28 34 19 25 26 23 20 18 24 21 22 14 27 12 11 17 10 15 9 16 1 7 8 5 2 0 6 3 4 13 38 44 45 42 39 37 43 40 41 29 35 36 33 30 28 34 31 32 26 20 23 18 21 24 22 25 19 27 11 10 13 14 12 17 16 9 8 2 5 0 3 6 4 7 1 15 45 39 42 37 40 43 41 44 38 36 30 33 28 31 34 32 35 29 23 21 18 24 25 22 19 20 26 16 13 14 15 11 9 27 10 17 5 3 0 6 7 4 1 2 8 12 42 40 37 43 44 41 38 39 45 33 31 28 34 35 32 29 30 36 37 43 44 41 38 39 45 42 40 28 34 35 32 29 30 36 33 31 18 23 27 19 24 26 22 21 20 25 9 15 16 13 10 11 17 14 12 0 6 7 4 1 2 8 5 3 44 38 41 39 42 45 40 43 37 35 29 32 30 33 36 31 34 28 20 19 22 25 18 27 23 24 21 26 16 10 13 11 14 17 12 15 9 7 1 4 2 5 8 3 6 0 41 42 39 45 43 40 37 38 44 32 33 30 36 34 31 28 29 35 19 26 20 27 21 22 25 23 24 18 13 14 11 17 15 12 9 10 16 4 5 2 8 6 3 0 1 7 39 45 43 40 37 38 44 41 42 30 36 34 31 28 29 35 32 33 22 24 26 21 25 20 18 27 19 23 11 17 15 12 9 10 16 13 14 2 8 6 3 0 1 7 4 5 43 37 40 38 41 44 42 45 39 34 28 31 29 32 35 33 36 30 21 25 18 23 22 24 19 26 27 20 15 9 12 10 13 16 14 17 11 6 0 3 1 4 7 5 8 2 40 41 38 44 45 42 39 37 43 31 32 29 35 36 33 30 28 34 24 18 25 26 27 23 21 20 22 19 12 13 10 16 17 14 11 9 15 3 4 1 7 8 5 2 0 6 38 44 45 42 39 37 43 40 41 29 35 36 33 30 28 34 31 32 23 27 21 20 26 19 24 18 25 22 10 16 17 14 11 9 15 12 13 1 7 8 5 2 0 6 3 4 45 39 42 37 40 43 41 44 38 36 30 33 28 31 34 32 35 29 27 20 19 22 23 21 26 25 18 24 17 11 14 9 12 15 13 16 10 8 2 5 0 3 6 4 7 1 42 40 37 43 44 41 38 39 45 33 31 28 34 35 32 29 30 36 25 22 23 24 20 18 27 19 26 21 14 12 9 15 16 13 10 11 17 5 3 0 6 7 4 1 2 8 8 3 6 0 1 7 2 4 5 17 12 15 9 10 16 11 13 14 26 21 24 18 19 25 20 22 23 27 36 31 34 28 29 35 30 32 33 45 40 43 37 38 44 39 41 42 9 15 16 13 10 11 17 14 12 0 6 7 4 1 2 8 5 3 37 43 44 41 38 39 45 42 40 35 28 33 27 29 34 36 32 31 30 18 24 25 22 19 20 26 23 21 16 10 13 11 14 17 12 15 9 7 1 4 2 5 8 3 6 0 44 38 41 39 42 45 40 43 37 36 30 29 32 35 28 27 33 34 31 25 19 22 20 23 26 21 24 18 13 14 11 17 15 12 9 10 16 4 5 2 8 6 3 0 1 7 41 42 39 45 43 40 37 38 44 28 29 36 30 27 31 32 35 33 34 22 23 20 26 24 21 18 19 25 11 17 15 12 9 10 16 13 14 2 8 6 3 0 1 7 4 5 39 45 43 40 37 38 44 41 42 33 32 34 36 31 35 30 28 27 29 20 26 24 21 18 19 25 22 23 15 9 12 10 13 16 14 17 11 6 0 3 1 4 7 5 8 2 43 37 40 38 41 44 42 45 39 30 31 35 28 33 32 34 29 36 27 24 18 21 19 22 25 23 26 20 12 13 10 16 17 14 11 9 15 3 4 1 7 8 5 2 0 6 40 41 38 44 45 42 39 37 43 29 34 28 35 36 27 33 31 30 32 21 22 19 25 26 23 20 18 24 10 16 17 14 11 9 15 12 13 1 7 8 5 2 0 6 3 4 38 44 45 42 39 37 43 40 41 32 33 27 31 30 36 29 34 28 35 19 25 26 23 20 18 24 21 22 17 11 14 9 12 15 13 16 10 8 2 5 0 3 6 4 7 1 45 39 42 37 40 43 41 44 38 34 27 30 29 32 33 31 36 35 28 26 20 23 18 21 24 22 25 19 14 12 9 15 16 13 10 11 17 5 3 0 6 7 4 1 2 8 42 40 37 43 44 41 38 39 45 31 35 32 33 34 30 28 27 29 36 23 21 18 24 25 22 19 20 26 28 34 35 32 29 30 36 33 31 18 24 25 22 19 20 26 23 21 9 15 16 13 10 11 17 14 12 44 0 6 7 4 1 2 8 5 3 37 42 27 38 43 45 41 40 39 35 29 32 30 33 36 31 34 28 25 19 22 20 23 26 21 24 18 16 10 13 11 14 17 12 15 9 45 7 1 4 2 5 8 3 6 0 39 38 41 44 37 27 42 43 40 32 33 30 36 34 31 28 29 35 22 23 20 26 24 21 18 19 25 13 14 11 17 15 12 9 10 16 37 4 5 2 8 6 3 0 1 7 38 45 39 27 40 41 44 42 43 30 36 34 31 28 29 35 32 33 20 26 24 21 18 19 25 22 23 11 17 15 12 9 10 16 13 14 42 2 8 6 3 0 1 7 4 5 41 43 45 40 44 39 37 27 38 34 28 31 29 32 35 33 36 30 24 18 21 19 22 25 23 26 20 15 9 12 10 13 16 14 17 11 39 6 0 3 1 4 7 5 8 2 40 44 37 42 41 43 38 45 27 31 32 29 35 36 33 30 28 34 21 22 19 25 26 23 20 18 24 12 13 10 16 17 14 11 9 15 38 3 4 1 7 8 5 2 0 6 43 37 44 45 27 42 40 39 41 29 35 36 33 30 28 34 31 32 19 25 26 23 20 18 24 21 22 10 16 17 14 11 9 15 12 13 41 1 7 8 5 2 0 6 3 4 42 27 40 39 45 38 43 37 44 36 30 33 28 31 34 32 35 29 26 20 23 18 21 24 22 25 19 17 11 14 9 12 15 13 16 10 43 8 2 5 0 3 6 4 7 1 27 39 38 41 42 40 45 44 37 33 31 28 34 35 32 29 30 36 23 21 18 24 25 22 19 20 26 14 12 9 15 16 13 10 11 17 40 5 3 0 6 7 4 1 2 8 44 41 42 43 39 37 27 38 45 Программа Harry White - высший пилотаж! Напомню: это у Harry метод SODLS для построения магических квадратов. А магический квадрат он и строит с помощью полученной ортогональной пары ДЛК. Все отсутствующие ортогональные пары для ДЛК порядков n<=50 найдены. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Вот нашла тут, в теме ассоциативный SODLS 16-го порядка Я тут программу Tomas Brada ortogonb.exe осваиваю :) (смотрите тут) Вот для показанного в цитате ДЛК посчитала по этой программе количество Д-трансверсалей. Что-то жутко много получилось: 31313088 Д-трансверсалей. Засомневалась, правильно ли программа насчитала... Может быть, я что-то сделала не так. Хотя квадратик офигенный, вполне может быть, что и имеет так много Д-трансверсалей. Кстати, надо было применить режим "посчитать трансверсали и выйти", потому что программа пошла дальше - искать ортогональные соквадраты и зависла. У Tomas Brada есть такой ДЛК 16-го порядка HJUmgVNZQnTeguW9hVu4wbEppeo5hqYHNDP2hXm3qrnLkfL7mWD3KT8i7nrSmA62pM5 (16, 15456144, ?) отсюда https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4133 Для этого ДЛК я просила Harry White посчитать количество Д-трансверсалей, он посчитал, результат такой же, как у Tomas Brada - 15456144. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сейчас применила режим "посчитать трансверсали". Протокол работы программы C:\Users\Дом\Downloads\libr>ortogonb.exe -c H8YURdMXZnihqsPkArWe9CwrZqH62bHYQ3MY 81AmSxkqDU4UM8WFe3ncZMbpZr5 1>out.txt init_trans(16) used 851 nodes dance_mt: using 2 threads for 16 rows in column 1 l(1) 16 / 16 Программа вывела в файл out.txt num_dtrans: 31313088 По идее должно быть правильно. Это максимальное количество Д-трансверсалей для ДЛК 16-го порядка, известное мне на данный момент. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Нет, для ассоциативного SODLS 17-го порядка программа Harry что-то задумалась. Для этого классного квадратика тоже посчитала количество трансверсалей по программе Tomas Brada. Протокол работы программы C:\Users\Дом\Downloads\libr>ortogonb.exe -c JQiBJzfpi4cDA7gjVeqHYS9v66FyyHaywfvh UvgBXnkJa2PbDv7UgMAgKYZupiCsckFX7b8kMdaEFFREt4gbPtRSf2 1>out.txt init_trans(17) used 955 nodes dance_mt: using 2 threads for 17 rows in column 1 l(1) 17 / 17 Результат записан в файл out.txt num_dtrans: 204995269 Это текущий максимум количества Д-трансверсалей для ДЛК 17-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Если всё правильно насчитала, тогда имеем для последовательности OEIS https://oeis.org/A287648 следующие оценки a(16) >= 31313088, a(17) >= 204995269 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Для ДЛК 18-го порядка насчитала 280308432 Д-трансверсалей. Считала для ДЛК, построенного методом Гергели 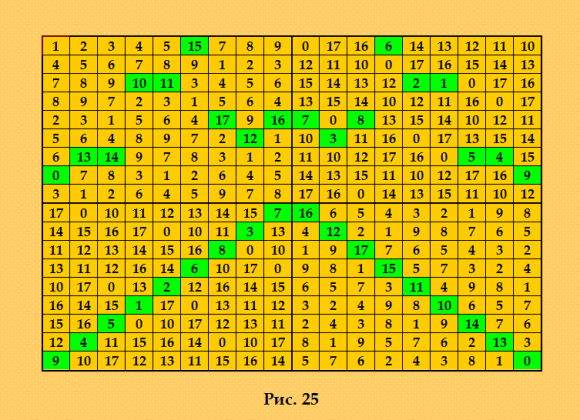 Это получилась у меня оценка для a(18) a(18) >= 280308432 У Tomas Brada имеется (ссылка указана выше) KUwuJ8TaFRKk82ckNomJHbJdRHUUzx413PBL1dq7WqLTqyLPR4paqjGSU2xcuJrfQ6bb4UVn3pVZLYHLLQkd53jhhiwedC (18, 82602438, ?) LhDfWkfWNWsfvUzFYyyvx5AqBgSFywEfyHwEYKZiydespqiN347Rwa971usDASx45jxmGzb8ssC99X3tviY3jb3Sgkr6Sz9jnZcRKLK (19, 631935677, ?) Ну, для ДЛК 18-го порядка у него мало Д-трансверсалей. А вот для ДЛК порядка 19, наверное, текущий максимум. Я пока не считала для ДЛК этого порядка. Кстати, ДЛК Гергели в закодированном по системе Tomas Brada виде выглядит так KXz98jHe3xqNgKno4EZyrPSQpj5Mu8Y6A5wx1U4FWZWTVE46spXG8qXAJD7W6fuK8kCSqMcPTTHspANa1A4Mn4gVEph4 В этой системе, как я понимаю, первой символ имени означает порядок квадрата: J <-->17, K <--> 18, L <--> 19 и т. д. PS. А квадрат 19-го порядка у Tomas Brada - тоже квадрат Гергели. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Решила в этом ДЛК 19-го порядка посчитать Д-трансверсали 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 ДЛК из полной системы MOLS, построен вручную методом циклического сдвига. Утилита Harry White сообщает об этом ДЛК Order? 19
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
1 diagonal Latin
1 pandiagonal
1 center symmetric
1 nfr
1 self-orthogonalЗапустила программу C:\Users\Дом\Downloads\libr>ortogonb.exe -c LNPBNdjGWMGj8q6LJcFJQDE9d3bfxZxELHin jkmjZp9FAqyy8P8Byyzks9rAa4GSffr4GSWyqqvwagd8aKGotS6KZZhYQ1KhesT4XnarJWF83MvkwohS EvKg3 1>out.txt init_trans(19) used 1181 nodes dance_mt: using 2 threads for 19 rows in column 1 ... Жду. Ой, ни фига не дождалась, вот это выдалось C:\Users\Дом\Downloads\libr>ortogonb.exe -c LNPBNdjGWMGj8q6LJcFJQDE9d3bfxZxELHin jkmjZp9FAqyy8P8Byyzks9rAa4GSffr4GSWyqqvwagd8aKGotS6KZZhYQ1KhesT4XnarJWF83MvkwohS EvKg3 1>out.txt init_trans(19) used 1181 nodes dance_mt: using 2 threads for 19 rows in column 1 l(1) 2 / 19 и дальше не хочет выдавать. При этом занимает два потока и у меня другая программа почти стоит. Поэтому прерываю. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger