ОДЛК для порядков n>10


Advanced search

Message boards : Science : ОДЛК для порядков n>10
Message board moderation

To post messages, you must log in.

Previous · 1 . . . 20 · 21 · 22 · 23 · 24 · 25 · 26 . . . 27 · Next

AuthorMessage
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6453 - Posted: 30 Sep 2020, 18:49:16 UTC
Last modified: 30 Sep 2020, 18:50:09 UTC

Для порядков 21 и 22 SODLS у меня нет.
А для порядка 23 - вот они
цитирую
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7
10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9
12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11
14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13
16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6
9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8
11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10
13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12
15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2
6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5
9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8
12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11
15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3
7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6
10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9
13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12
16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1
5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4
8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7
11 12 13 14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10
14 15 16 17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13
17 18 19 20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
20 21 22 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

Утилита Harry White сообщает от этих ОДЛК следуюшее:
Thursday 2020-06-18 07:45:45 ╠юёъютёъюх тЁхь  (чшьр)

Order? 23

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt

Counts
------
         2 diagonal Latin
         2 pandiagonal
         2 center symmetric
         2 nfr
         1 orthogonal pair
         2 self-orthogonal

Отличные свойства!
Квадраты ассоциативные и пандиагональные (то есть ultra), ещё они self orthogonal.

Построены методом циклического сдвига.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6453 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6455 - Posted: 1 Oct 2020, 5:03:13 UTC
Last modified: 1 Oct 2020, 5:19:35 UTC

Программку для построения antitranspose сварганила.
Теперь проверю.
На этом симпатяге я остановилась

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1
4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3
6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5
8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7
10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9
12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11
14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13
16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0
3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2
5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4
7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6
9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8
11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10
13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12
15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14

это atnitranspose

 14  12  10  8  6  4  2  0  15  13  11  9  7  5  3  1  16 
 13  11  9  7  5  3  1  16  14  12  10  8  6  4  2  0  15 
 12  10  8  6  4  2  0  15  13  11  9  7  5  3  1  16  14 
 11  9  7  5  3  1  16  14  12  10  8  6  4  2  0  15  13 
 10  8  6  4  2  0  15  13  11  9  7  5  3  1  16  14  12 
 9  7  5  3  1  16  14  12  10  8  6  4  2  0  15  13  11 
 8  6  4  2  0  15  13  11  9  7  5  3  1  16  14  12  10 
 7  5  3  1  16  14  12  10  8  6  4  2  0  15  13  11  9 
 6  4  2  0  15  13  11  9  7  5  3  1  16  14  12  10  8 
 5  3  1  16  14  12  10  8  6  4  2  0  15  13  11  9  7 
 4  2  0  15  13  11  9  7  5  3  1  16  14  12  10  8  6 
 3  1  16  14  12  10  8  6  4  2  0  15  13  11  9  7  5 
 2  0  15  13  11  9  7  5  3  1  16  14  12  10  8  6  4 
 1  16  14  12  10  8  6  4  2  0  15  13  11  9  7  5  3 
 0  15  13  11  9  7  5  3  1  16  14  12  10  8  6  4  2 
 16  14  12  10  8  6  4  2  0  15  13  11  9  7  5  3  1 
 15  13  11  9  7  5  3  1  16  14  12  10  8  6  4  2  0

Проверяю на ортогональность симпатягу и его atnitranspose
Order? 17

Enter the name of the squares file: inp
..output file inpPairs_4.txt
..output file inpPairNos_5.txt
squares 2 orthogonal pairs 1

Всё в порядке, квадраты ортогональны.

А для порядка 18 SODLS не ассоциативные (ассоциативных для данного порядка не может быть).
Но на DSODLS надо проверить, DSODLS бывают и не ассоциативные.

Проверила. Нет, не являются два мои SODLS 18-го порядка DSODLS.
На очереди ассоциативный SODLS 19-го порядка.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6455 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6456 - Posted: 1 Oct 2020, 5:27:58 UTC

Исходный ДЛК
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1
4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3
6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5
8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7
10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9
12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11
14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13
16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0
3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2
5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4
7 8 9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6
9 10 11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8
11 12 13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10
13 14 15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12
15 16 17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14
17 18 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

antitranspoze
 16  14  12  10  8  6  4  2  0  17  15  13  11  9  7  5  3  1  18 
 15  13  11  9  7  5  3  1  18  16  14  12  10  8  6  4  2  0  17 
 14  12  10  8  6  4  2  0  17  15  13  11  9  7  5  3  1  18  16 
 13  11  9  7  5  3  1  18  16  14  12  10  8  6  4  2  0  17  15 
 12  10  8  6  4  2  0  17  15  13  11  9  7  5  3  1  18  16  14 
 11  9  7  5  3  1  18  16  14  12  10  8  6  4  2  0  17  15  13 
 10  8  6  4  2  0  17  15  13  11  9  7  5  3  1  18  16  14  12 
 9  7  5  3  1  18  16  14  12  10  8  6  4  2  0  17  15  13  11 
 8  6  4  2  0  17  15  13  11  9  7  5  3  1  18  16  14  12  10 
 7  5  3  1  18  16  14  12  10  8  6  4  2  0  17  15  13  11  9 
 6  4  2  0  17  15  13  11  9  7  5  3  1  18  16  14  12  10  8 
 5  3  1  18  16  14  12  10  8  6  4  2  0  17  15  13  11  9  7 
 4  2  0  17  15  13  11  9  7  5  3  1  18  16  14  12  10  8  6 
 3  1  18  16  14  12  10  8  6  4  2  0  17  15  13  11  9  7  5 
 2  0  17  15  13  11  9  7  5  3  1  18  16  14  12  10  8  6  4 
 1  18  16  14  12  10  8  6  4  2  0  17  15  13  11  9  7  5  3 
 0  17  15  13  11  9  7  5  3  1  18  16  14  12  10  8  6  4  2 
 18  16  14  12  10  8  6  4  2  0  17  15  13  11  9  7  5  3  1 
 17  15  13  11  9  7  5  3  1  18  16  14  12  10  8  6  4  2  0

Проверка на ортогональность

Order? 19

Enter the name of the squares file: inp
..output file inpPairs_3.txt
..output file inpPairNos_3.txt
squares 2 orthogonal pairs 1

Всё в порядке, квадраты ортогональны.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6456 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6457 - Posted: 1 Oct 2020, 5:35:18 UTC

Для порядка 20

исходный ДЛК
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
2 3 4 0 1 7 8 9 5 6 12 13 14 10 11 17 18 19 15 16
4 0 1 2 3 9 5 6 7 8 14 10 11 12 13 19 15 16 17 18
1 2 3 4 0 6 7 8 9 5 11 12 13 14 10 16 17 18 19 15
3 4 0 1 2 8 9 5 6 7 13 14 10 11 12 18 19 15 16 17
15 16 17 18 19 10 11 12 13 14 5 6 7 8 9 0 1 2 3 4
17 18 19 15 16 12 13 14 10 11 7 8 9 5 6 2 3 4 0 1
19 15 16 17 18 14 10 11 12 13 9 5 6 7 8 4 0 1 2 3
16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 0
18 19 15 16 17 13 14 10 11 12 8 9 5 6 7 3 4 0 1 2
5 6 7 8 9 0 1 2 3 4 15 16 17 18 19 10 11 12 13 14
7 8 9 5 6 2 3 4 0 1 17 18 19 15 16 12 13 14 10 11
9 5 6 7 8 4 0 1 2 3 19 15 16 17 18 14 10 11 12 13
6 7 8 9 5 1 2 3 4 0 16 17 18 19 15 11 12 13 14 10
8 9 5 6 7 3 4 0 1 2 18 19 15 16 17 13 14 10 11 12
10 11 12 13 14 15 16 17 18 19 0 1 2 3 4 5 6 7 8 9
12 13 14 10 11 17 18 19 15 16 2 3 4 0 1 7 8 9 5 6
14 10 11 12 13 19 15 16 17 18 4 0 1 2 3 9 5 6 7 8
11 12 13 14 10 16 17 18 19 15 1 2 3 4 0 6 7 8 9 5
13 14 10 11 12 18 19 15 16 17 3 4 0 1 2 8 9 5 6 7

antitranspose
 7  5  8  6  9  12  10  13  11  14  2  0  3  1  4  17  15  18  16  19 
 6  9  7  5  8  11  14  12  10  13  1  4  2  0  3  16  19  17  15  18 
 5  8  6  9  7  10  13  11  14  12  0  3  1  4  2  15  18  16  19  17 
 9  7  5  8  6  14  12  10  13  11  4  2  0  3  1  19  17  15  18  16 
 8  6  9  7  5  13  11  14  12  10  3  1  4  2  0  18  16  19  17  15 
 2  0  3  1  4  17  15  18  16  19  7  5  8  6  9  12  10  13  11  14 
 1  4  2  0  3  16  19  17  15  18  6  9  7  5  8  11  14  12  10  13 
 0  3  1  4  2  15  18  16  19  17  5  8  6  9  7  10  13  11  14  12 
 4  2  0  3  1  19  17  15  18  16  9  7  5  8  6  14  12  10  13  11 
 3  1  4  2  0  18  16  19  17  15  8  6  9  7  5  13  11  14  12  10 
 17  15  18  16  19  2  0  3  1  4  12  10  13  11  14  7  5  8  6  9 
 16  19  17  15  18  1  4  2  0  3  11  14  12  10  13  6  9  7  5  8 
 15  18  16  19  17  0  3  1  4  2  10  13  11  14  12  5  8  6  9  7 
 19  17  15  18  16  4  2  0  3  1  14  12  10  13  11  9  7  5  8  6 
 18  16  19  17  15  3  1  4  2  0  13  11  14  12  10  8  6  9  7  5 
 12  10  13  11  14  7  5  8  6  9  17  15  18  16  19  2  0  3  1  4 
 11  14  12  10  13  6  9  7  5  8  16  19  17  15  18  1  4  2  0  3 
 10  13  11  14  12  5  8  6  9  7  15  18  16  19  17  0  3  1  4  2 
 14  12  10  13  11  9  7  5  8  6  19  17  15  18  16  4  2  0  3  1 
 13  11  14  12  10  8  6  9  7  5  18  16  19  17  15  3  1  4  2  0

Проверка
Order? 20

Enter the name of the squares file: inp
..output file inpPairs_3.txt
..output file inpPairNos_3.txt
squares 2 orthogonal pairs 1

Квадраты ортогональны.

А что с красавцем 20-го порядка, он не ассоциативный SODLS.
Сейчас посмотрим, вряд ли будет DSODLS.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6457 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6458 - Posted: 1 Oct 2020, 5:38:03 UTC
Last modified: 1 Oct 2020, 5:44:07 UTC

Итак, исходный ДЛК



antitranspose
 19  9  4  14  10  0  16  6  12  2  8  18  15  5  1  11  7  17  3  13 
 8  18  15  5  1  11  7  17  3  13  19  9  4  14  10  0  16  6  12  2 
 1  11  17  7  2  12  8  18  14  4  10  0  6  16  13  3  19  9  5  15 
 10  0  6  16  13  3  19  9  5  15  1  11  17  7  2  12  8  18  14  4 
 3  13  19  9  15  5  0  10  6  16  12  2  8  18  4  14  11  1  17  7 
 12  2  8  18  4  14  11  1  17  7  3  13  19  9  15  5  0  10  6  16 
 15  5  1  11  17  7  13  3  18  8  4  14  10  0  6  16  2  12  9  19 
 4  14  10  0  6  16  2  12  9  19  15  5  1  11  17  7  13  3  18  8 
 7  17  13  3  19  9  15  5  11  1  16  6  2  12  8  18  4  14  0  10 
 16  6  2  12  8  18  4  14  0  10  7  17  13  3  19  9  15  5  11  1 
 18  8  5  15  11  1  17  7  13  3  9  19  14  4  0  10  6  16  2  12 
 9  19  14  4  0  10  6  16  2  12  18  8  5  15  11  1  17  7  13  3 
 0  10  16  6  3  13  9  19  15  5  11  1  7  17  12  2  18  8  4  14 
 11  1  7  17  12  2  18  8  4  14  0  10  16  6  3  13  9  19  15  5 
 2  12  18  8  14  4  1  11  7  17  13  3  9  19  5  15  10  0  16  6 
 13  3  9  19  5  15  10  0  16  6  2  12  18  8  14  4  1  11  7  17 
 14  4  0  10  16  6  12  2  19  9  5  15  11  1  7  17  3  13  8  18 
 5  15  11  1  7  17  3  13  8  18  14  4  0  10  16  6  12  2  19  9 
 6  16  12  2  18  8  14  4  10  0  17  7  3  13  9  19  5  15  1  11 
 17  7  3  13  9  19  5  15  1  11  6  16  12  2  18  8  14  4  10  0

Проверка
Order? 20

Enter the name of the squares file: inp
..output file inpPairs_3.txt
..output file inpPairNos_3.txt
squares 2 orthogonal pairs 1

Является DSODLS!
Очень интересный квадрат.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6458 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6459 - Posted: 1 Oct 2020, 5:53:16 UTC

До порядка 20 всё проверила.
Гипотеза пока подтверждается для всех ассоциативных SODLS - все они также и DSODLS.
Кажется, интуитивно и понятно - за счёт ассоциативности всё получается.
Но надо строго доказать, интуиция - не доказательство.

С порядком 21 что-то не везёт. Вчера покрутила программу Harry White для диагонали 1, не нашла решение.
Сегодня покрутила для диагонали 3
SODLS order? 21

Make SSSOLDS, y (yes) or n (no)? y
.. writing SODLS to file SSSODLS21_1.txt
First /diagonal value, (1..9 or 11..19)? 3

не находится решение.
Ну, порядок 21 вообще сильно проблемный. У меня здесь, кажется, нет ни одной ортогональной пары ДЛК данного порядка.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6459 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6461 - Posted: 2 Oct 2020, 1:55:22 UTC

У меня хорошая новость.
Harry White прислал программки для разных поворотов.
Цитата
Program http://budshaw.ca/Download.html#rotate
will make these.

transpose = rotate 7, anti-transpose = rotate 5

Я скачала и попробовала. Отлично работают программки.
Теперь можно крутить-вертеть квадраты :)

Например, транспонированнный вариант для ДЛК 20-го порядка, полученный программой Harry

 0  2  4  1  3 15 17 19 16 18  5  7  9  6  8 10 12 14 11 13
 1  3  0  2  4 16 18 15 17 19  6  8  5  7  9 11 13 10 12 14
 2  4  1  3  0 17 19 16 18 15  7  9  6  8  5 12 14 11 13 10
 3  0  2  4  1 18 15 17 19 16  8  5  7  9  6 13 10 12 14 11
 4  1  3  0  2 19 16 18 15 17  9  6  8  5  7 14 11 13 10 12
 5  7  9  6  8 10 12 14 11 13  0  2  4  1  3 15 17 19 16 18
 6  8  5  7  9 11 13 10 12 14  1  3  0  2  4 16 18 15 17 19
 7  9  6  8  5 12 14 11 13 10  2  4  1  3  0 17 19 16 18 15
 8  5  7  9  6 13 10 12 14 11  3  0  2  4  1 18 15 17 19 16
 9  6  8  5  7 14 11 13 10 12  4  1  3  0  2 19 16 18 15 17
10 12 14 11 13  5  7  9  6  8 15 17 19 16 18  0  2  4  1  3
11 13 10 12 14  6  8  5  7  9 16 18 15 17 19  1  3  0  2  4
12 14 11 13 10  7  9  6  8  5 17 19 16 18 15  2  4  1  3  0
13 10 12 14 11  8  5  7  9  6 18 15 17 19 16  3  0  2  4  1
14 11 13 10 12  9  6  8  5  7 19 16 18 15 17  4  1  3  0  2
15 17 19 16 18  0  2  4  1  3 10 12 14 11 13  5  7  9  6  8
16 18 15 17 19  1  3  0  2  4 11 13 10 12 14  6  8  5  7  9
17 19 16 18 15  2  4  1  3  0 12 14 11 13 10  7  9  6  8  5
18 15 17 19 16  3  0  2  4  1 13 10 12 14 11  8  5  7  9  6
19 16 18 15 17  4  1  3  0  2 14 11 13 10 12  9  6  8  5  7
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6461 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6464 - Posted: 2 Oct 2020, 9:48:07 UTC

Приведу цитату из своей статьи (ссылка на статью в подписи к посту)

A Doubly Self Orthogonal Latin Square (DSOLS) is a Latin square which is orthogonal to its transpose to the diagonal and its transpose to the back diagonal. It is challenging to find a non-trivial DSOLS. For the orders n = 2 (mod 4), the existence of DSOLS(n) is unknown except for n = 2, 6. We propose an efficient approach and data structure based on a set system and exact cover, with which we obtained a new result, i.e., the non-existence of DSOLS(10).

As I understand it, this is from the next book
«Principles and Practice of Constraint Programming – CP 2011»
https://link.springer.com/book/10.1007/978-3-642-23786-7


Порядки серии n=2(mod 4) проблемные для DSOLS, а значит и для DSODLS.
Для порядка 14 я даже SODLS пока не нашла.
А вот для порядка 18 уже есть SODLS (см. выше).
Дальше ещё не искала.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6464 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6486 - Posted: 3 Oct 2020, 16:56:39 UTC
Last modified: 3 Oct 2020, 16:58:17 UTC

У меня отличная новость.
Harry White прислал SODLS порядков 14 и 21.
Сначала покажу два SODLS порядка 14

 0 12  6 10  9 13 11  2  1  5  8  7  4  3
 8  1 10  7  6  9 12  4  0  3 11 13  2  5
 4  5  2  9  7 11 13  0  3  1 12 10  8  6
 6 10  8  3  5  4  0 13  2  7  1 12  9 11
 5 13  3  0  4 12  2 10  9 11  7  1  6  8
10  0 12  2  1  5  7  8  6 13  3  9 11  4
 1  2  9 11  0  8  6  5  7 12  4  3 13 10
 3 11 13 12  2  6  8  7  5  4  9  0 10  1
 2  3 11 13 12  7  5  6  8 10  0  4  1  9
11  8  5  1 13  3 10 12  4  9  6  2  0  7
13  6  7  4 11  1  9  3 12  0 10  8  5  2
 9  7  0  5  8 10  4  1 13  6  2 11  3 12
 7  9  4  6  3  2  1 11 10  8 13  5 12  0
12  4  1  8 10  0  3  9 11  2  5  6  7 13

 0 12  9  6  5  1 13  2  3  8  7  4 11 10
 5  1  0  2  6 11 12  4 13  7  3 10  9  8
 6  5  2 11 12  3  9 10  4  1  0 13  8  7
11  6  5  3 13 10  2  9  1  4 12  8  7  0
 9 13  6  5  4 12  0  1 10 11  8  7  2  3
 3  2 11  1 10  5  8  6  7 12 13  0  4  9
 1  4 10  9  3  7  6  8  5  0 11 12 13  2
 4 10 13 12  0  8  5  7  6  2  9  1  3 11
10  0  3  4 11  6  7  5  8 13  2  9  1 12
12 11  7  8  1 13 10  3  2  9  5  6  0  4
13  7  8  0  2  9  4 11 12  3 10  5  6  1
 7  8  4 13  9  2  3 12  0 10  1 11  5  6
 8  3  1 10  7  0 11 13  9  6  4  2 12  5
 2  9 12  7  8  4  1  0 11  5  6  3 10 13

О SODLS 21-го порядка подумала, что он ассоциативный (ассоциативный проще искать), но нет

 0 12  3  2 17 19 20 18 13 15 16 14  1  8 10 11  9  4  6  7  5
 2  1  0 12 20 18 17 19 16 14 13 15  3 11  9  8 10  7  5  4  6
12  3  2  1 18 20 19 17 14 16 15 13  0  9 11 10  8  5  7  6  4
 1  0 12  3 19 17 18 20 15 13 14 16  2 10  8  9 11  6  4  5  7
 8 10 11  9  4 12  7  6  0  2  3  1  5 17 19 20 18 13 15 16 14
11  9  8 10  6  5  4 12  3  1  0  2  7 20 18 17 19 16 14 13 15
 9 11 10  8 12  7  6  5  1  3  2  0  4 18 20 19 17 14 16 15 13
10  8  9 11  5  4 12  7  2  0  1  3  6 19 17 18 20 15 13 14 16
17 19 20 18 13 15 16 14  8 12 11 10  9  4  6  7  5  0  2  3  1
20 18 17 19 16 14 13 15 10  9  8 12 11  7  5  4  6  3  1  0  2
18 20 19 17 14 16 15 13 12 11 10  9  8  5  7  6  4  1  3  2  0
19 17 18 20 15 13 14 16  9  8 12 11 10  6  4  5  7  2  0  1  3
 3  2  1  0  7  6  5  4 11 10  9  8 12 16 15 14 13 20 19 18 17
 4  6  7  5  0  2  3  1 17 19 20 18 14 13 12 16 15  8 10 11  9
 7  5  4  6  3  1  0  2 20 18 17 19 16 15 14 13 12 11  9  8 10
 5  7  6  4  1  3  2  0 18 20 19 17 13 12 16 15 14  9 11 10  8
 6  4  5  7  2  0  1  3 19 17 18 20 15 14 13 12 16 10  8  9 11
13 15 16 14  8 10 11  9  4  6  7  5 18  0  2  3  1 17 12 20 19
16 14 13 15 11  9  8 10  7  5  4  6 20  3  1  0  2 19 18 17 12
14 16 15 13  9 11 10  8  5  7  6  4 17  1  3  2  0 12 20 19 18
15 13 14 16 10  8  9 11  6  4  5  7 19  2  0  1  3 18 17 12 20

Проверка этого ДЛК утилитой Harry GetType
Order? 21

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         1 diagonal Latin
         1 natural \diagonal
         1 self-orthogonal

SODLS не ассоциативный и DSODLS не является.
А я подумала сначала, что найден контрпример: ассоциативный SODLS не является DSODLS.
Пока контрпримера у меня нет.

У нас теперь есть одна ортогональная пара ДЛК 21-го порядка!
Замечательно. Ликвидировали одно белое пятно.

И теперь у нас есть SODLS для порядков n<24 за исключением n=22.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6486 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6492 - Posted: 3 Oct 2020, 18:13:41 UTC

О-о-о!
Пришло некоторое уточнение от Harry White.
Цитирую
I was referring to program MagicSquaresSODLS http://budshaw.ca/Download.html#sodls
It will instantly make a SODLS of any order, (except 2, 3, 6).


Я и не сразу поняла, что есть другая программа для построения SODLS.
На основе пары из SODLS мгновенно получается магический квадрат.

Скачала и попробовала для порядка 22.
Мгновенно получила SODLS и магический квадрат, полученный с его помощью (магический квадрат не показываю)

 0 16 14  8 15  6 17 10  9  1 21  2  3 12 11  5 20 19  4 13  7 18
 9  1 15 13  0 14  7 16 10  2 20  3  4 11  6 19 18  5 21  8 17 12
10  9  2 14 21  1 13  8 15  3 19  4  5  7 18 17  6 20  0 16 12 11
14 10  9  3 13 20  2 21  0  4 18  5  6 17 16  7 19  1 15 12 11  8
 1 13 10  9  4 21 19  3 20  5 17  6  7 15  8 18  2 14 12 11  0 16
19  2 21 10  9  5 20 18  4  6 16  7  8  0 17  3 13 12 11  1 15 14
 5 18  3 20 10  9  6 19 17  7 15  8  0 16  4 21 12 11  2 14 13  1
16  6 17  4 19 10  9  7 18  8 14  0  1  5 20 12 11  3 13 21  2 15
17 15  7 16  5 18 10  9  8  0 13  1  2 19 12 11  4 21 20  3 14  6
 3  4  5  6  7  8  0  1  2  9 11 12 10 21 13 14 15 16 17 18 19 20
20 19 18 17 16 15 14 13 21 12 10  9 11  2  1  0  8  7  6  5  4  3
21 20 19 18 17 16 15 14 13 10 12 11  9  1  0  8  7  6  5  4  3  2
 4  5  6  7  8  0  1  2  3 11  9 10 12 14 15 16 17 18 19 20 21 13
18  7 20 21  2  4 11 12  1 19  5 14 17 13  9 10  3  8 16 15  6  0
 6 21 13  1  3 11 12  0 19 20  4 15 18  8 14  9 10  2  7 17 16  5
13 14  0  2 11 12  8 20  5 21  3 16 19  4  7 15  9 10  1  6 18 17
15  8  1 11 12  7 21  4 14 13  2 17 20 18  3  6 16  9 10  0  5 19
 7  0 11 12  6 13  3 15 16 14  1 18 21 20 19  2  5 17  9 10  8  4
 8 11 12  5 14  2 16 17  6 15  0 19 13  3 21 20  1  4 18  9 10  7
11 12  4 15  1 17 18  5  7 16  8 20 14  6  2 13 21  0  3 19  9 10
12  3 16  0 18 19  4  6 11 17  7 21 15 10  5  1 14 13  8  2 20  9
 2 17  8 19 20  3  5 11 12 18  6 13 16  9 10  4  0 15 14  7  1 21

Здорово!
Тогда не понятно, почему программа SODLS, специально предназначенная для построения SODLS, работает очень медленно для больших порядков.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6492 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6493 - Posted: 3 Oct 2020, 18:39:12 UTC
Last modified: 3 Oct 2020, 19:16:52 UTC

Ого!
SODLS 24-го порядка получился ассоциативный

 0 12  3  2 20 13 23 22  1 21 16 14 19 18 17  9  8 15 11 10  4  6  7  5
 2  1  0 12 22 21 20 13  3 23 18 17 16 14 19 11 10  9  8 15  7  5  4  6
12  3  2  1 13 23 22 21  0 20 14 19 18 17 16  8 15 11 10  9  5  7  6  4
 1  0 12  3 21 20 13 23  2 22 17 16 14 19 18 10  9  8 15 11  6  4  5  7
 8 13 11 10  4 14  7  6 17  9  0 15  3  2  5  1 20 22 23 21 16 12 19 18
10  9  8 13  6  5  4 14 19 11  2  1  0 15  7  3 23 21 20 22 18 17 16 12
13 11 10  9 14  7  6  5 16  8 15  3  2  1  4  0 21 23 22 20 12 19 18 17
 9  8 13 11  5  4 14  7 18 10  1  0 15  3  6  2 22 20 21 23 17 16 12 19
 3  2  1  0 11 10  9  8 12 14 23 22 21 20 15 13  7  6  5  4 19 18 17 16
11 10  9  8 23 22 21 20 15 13  7  6  5  4 12 14 19 18 17 16  3  2  1  0
20 14 23 22 16 15 19 18  5  1  8 10 11  9 21 17  4 12  7  6  0 13  3  2
22 21 20 14 18 17 16 15  7  3 11  9  8 10 23 19  6  5  4 12  2  1  0 13
14 23 22 21 15 19 18 17  4  0  9 11 10  8 20 16 12  7  6  5 13  3  2  1
21 20 14 23 17 16 15 19  6  2 10  8  9 11 22 18  5  4 12  7  1  0 13  3
23 22 21 20  7  6  5  4 13 15 19 18 17 16 14 12  3  2  1  0 11 10  9  8
 7  6  5  4 19 18 17 16 14 12  3  2  1  0 13 15 11 10  9  8 23 22 21 20
 4 15  7  6  0  2  3  1 21 17 20 12 23 22  9  5 16 13 19 18  8 14 11 10
 6  5  4 15  3  1  0  2 23 19 22 21 20 12 11  7 18 17 16 13 10  9  8 14
15  7  6  5  1  3  2  0 20 16 12 23 22 21  8  4 13 19 18 17 14 11 10  9
 5  4 15  7  2  0  1  3 22 18 21 20 12 23 10  6 17 16 13 19  9  8 14 11
16 18 19 17  8 12 11 10  9  5  4 13  7  6  1 21  0 14  3  2 20 15 23 22
19 17 16 18 10  9  8 12 11  7  6  5  4 13  3 23  2  1  0 14 22 21 20 15
17 19 18 16 12 11 10  9  8  4 13  7  6  5  0 20 14  3  2  1 15 23 22 21
18 16 17 19  9  8 12 11 10  6  5  4 13  7  2 22  1  0 14  3 21 20 15 23

Order? 24

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt

Counts
------
         1 diagonal Latin
         1 center symmetric
         1 self-orthogonal

Тоже мгновенно построился.
Сейчас мы его на DSODLS проверим.

Да! Он является DSODLS.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6493 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6497 - Posted: 3 Oct 2020, 19:18:17 UTC

Завтра посмотрю, для каких порядков у нас нет ни одной ортогональной пары.
Попробую с помощью SODLS найти их.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6497 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6513 - Posted: 4 Oct 2020, 4:37:56 UTC
Last modified: 4 Oct 2020, 4:43:51 UTC

Цитата
a(9) ≥ 323, a(10) ≥ 866, a(11) ≥ 4665, a(12) ≥ 8760, a(13) ≥ 131106, a(14) ≥ 364252, a(15) ≥ 389318.
отсюда
https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5902

На сегодня имеем следующие оценки
a(9) ≥ 333, a(10) ≥ 866, a(11) ≥ 4828, a(12) ≥ 24901, a(13) ≥ 131106, a(14) ≥ 364596, a(15) ≥ 389318

Вчера я попросила Harry White посчитать Д-трансверсали во всех найденных мной КФ ОДЛК 14-го порядка (5241 КФ).
У меня программа вчера полдня работала и не справилась. Уже поздно вечером прервала.
Он любезно выполнил мою просьбу.
Вот как у него отработала программа

order? 14
Type of Latin square, 1 LS or 2 DLS? 2
Get diagonal transversals, (Y or N)? Y
File name? CF14_all
.. writing counts to file 14Transversals.txt
DLS 4490 max transversals 364596

elapsed time 8:27:03

Даже на его мощном компьютере программа работала более 8 часов.
И вот найдена новая оценка для Д-трансверсалей ДЛК 14-го порядка.

Показываю ДЛК, имеющий 364596 Д-трансверсалей

 0  7  6 11  9  3  4  5  2 12 13  8 10  1
 6  1 11  5 10 12  2  3  9  7  4 13  0  8
 5 11  2 12  8  1  7 10  0  6  9  3 13  4
13  6  5  3  1 10  9 12  7  0  2  4  8 11
12  3 10  1  4 13  8  6 11  5  0  7  2  9
10 12  1  8  2  5 11 13  4  3  6  0  9  7
 9  2  7  0  5 11  6  8 13  4  1 10  3 12
 4 13  3  9  6  0 10  7  1  8 12  2 11  5
 2  4  9 10 11  6  1  0  8 13  7 12  5  3
 1 10  8 13 12  2  5  4  3  9 11  6  7  0
 3  5 12  7 13  8  0  1  6 11 10  9  4  2
 8  0 13  4  7  9  3  2 12 10  5 11  1  6
 7  9  0  6  3  4 13 11  5  2  8  1 12 10
11  8  4  2  0  7 12  9 10  1  3  5  6 13
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6513 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6514 - Posted: 4 Oct 2020, 5:11:10 UTC

Позже я покажу остальные ДЛК с максимальным на данный момент количеством Д-трансверсалей.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6514 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6516 - Posted: 4 Oct 2020, 10:21:40 UTC
Last modified: 4 Oct 2020, 15:06:53 UTC

Итак, показываю ДЛК, имеющие максимальное количество Д-трансвнрсалей на данный момент

1. n=9
Совершенный квадрат



Смотрите мою статью "Совершенные латинские квадраты (часть 1)", там есть ссылка на статью, в которой этот квадрат опубликован.

Вывод программы Белышева ortogon_u
Проверка ДЛК9 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 333
Соквадратов:     308

2. n=10
ДЛК Брауна

0 8 5 1 7 3 4 6 9 2
5 1 7 2 9 8 0 3 4 6
1 7 2 9 5 6 8 0 3 4
9 6 4 3 0 2 7 1 5 8
3 0 8 6 4 1 5 9 2 7
4 3 0 8 6 5 9 2 7 1
7 2 9 5 1 4 6 8 0 3
6 4 3 0 8 9 2 7 1 5
2 9 6 4 3 7 1 5 8 0
8 5 1 7 2 0 3 4 6 9

Из статьи
Brown et al. "Completion of the Spectrum of Orthogonal Diagonal Latin Squares". Lecture notes in pure and applied mathematics 139 (1992), 43-49.
Вывод программы Белышева ortogon_u
Проверка ДЛК10 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 866
Соквадратов:     4


Продолжение следует
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6516 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6517 - Posted: 4 Oct 2020, 10:36:05 UTC
Last modified: 4 Oct 2020, 15:03:32 UTC

3. n=11

0 1 2 3 4 5 6 7 8 9 10
1 2 3 5 6 9 7 10 0 4 8
7 10 8 0 3 1 5 9 6 2 4
3 5 9 4 10 6 8 0 2 7 1
4 6 7 10 1 8 2 3 9 0 5
5 9 4 6 8 7 0 1 3 10 2
10 8 0 1 5 2 9 4 7 3 6
6 7 10 8 2 0 3 5 4 1 9
8 0 1 2 9 3 4 6 10 5 7
2 3 5 9 7 4 10 8 1 6 0
9 4 6 7 0 10 1 2 5 8 3

Квадрат нашёл Tomas Brada, смотрите
https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4149

Вывод программы Белышева ortogon_u
Проверка ДЛК11 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 4828
Соквадратов:     32462
Время в сек:     8000

1 38 15 12        1 1 1 1 1

Для выхода нажмите любую клавишу:

Поиск выполнен до конца.
У ДЛК имеется 32462 ОДЛК.

4. n=12
Квадрат найден мной

0 9 7 6 10 3 2 11 4 1 8 5
10 1 0 11 5 9 4 3 7 8 6 2
4 11 2 1 7 6 10 8 5 3 9 0
5 8 10 3 2 1 7 9 0 6 11 4
2 6 5 9 4 8 0 1 10 11 3 7
1 2 9 0 8 5 11 10 3 4 7 6
9 5 3 7 1 10 6 0 11 2 4 8
3 10 11 4 9 0 8 7 6 5 2 1
11 0 6 2 3 7 1 4 8 10 5 9
7 3 4 8 0 11 5 6 2 9 1 10
6 7 8 5 11 4 9 2 1 0 10 3
8 4 1 10 6 2 3 5 9 7 0 11

Вывод программы Белышева ortogon_u
Проверка ДЛК12 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 24901
Соквадратов:     2010
Время в сек:     2025

1994 812 165 28 14 2

Программа прервана. Диагональных соквадратов будет много.

5. n=13
ДЛК из полной системы MOLS

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

Вывод программы Белышева ortogon_u
Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 131106
Соквадратов:     4937
Время в сек:     10270

Программа была прервана. Конечно, диагональных соквадратов будет больше.

6. n=14

 0  7  6 11  9  3  4  5  2 12 13  8 10  1
 6  1 11  5 10 12  2  3  9  7  4 13  0  8
 5 11  2 12  8  1  7 10  0  6  9  3 13  4
13  6  5  3  1 10  9 12  7  0  2  4  8 11
12  3 10  1  4 13  8  6 11  5  0  7  2  9
10 12  1  8  2  5 11 13  4  3  6  0  9  7
 9  2  7  0  5 11  6  8 13  4  1 10  3 12
 4 13  3  9  6  0 10  7  1  8 12  2 11  5
 2  4  9 10 11  6  1  0  8 13  7 12  5  3
 1 10  8 13 12  2  5  4  3  9 11  6  7  0
 3  5 12  7 13  8  0  1  6 11 10  9  4  2
 8  0 13  4  7  9  3  2 12 10  5 11  1  6
 7  9  0  6  3  4 13 11  5  2  8  1 12 10
11  8  4  2  0  7 12  9 10  1  3  5  6 13

Вывод программы Белышева ortogon_u
Проверка ДЛК14 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 364596
Соквадратов:     1
Время в сек:     380

25358 10401 3947 1403 267 60 13 3

Программа прервана, поиск не выполнялся.
Уже понятно, что это ОДЛК. Этот ОДЛК из моего набора КФ ОДЛК 14-го порядка.
Набор КФ на Д-трансверсали проверял Harry White своей программой.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6517 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6518 - Posted: 4 Oct 2020, 10:52:16 UTC
Last modified: 4 Oct 2020, 18:05:32 UTC

7. n=15
ДЛК, построенный методом Гергели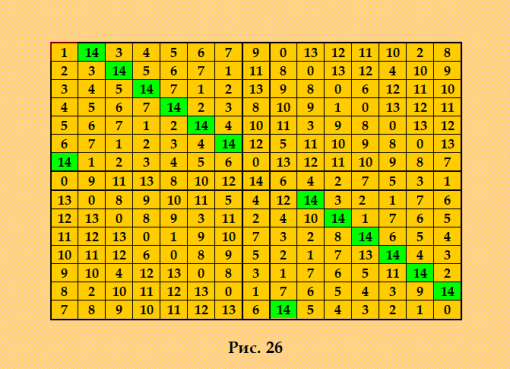


Смотрите мою статью
http://www.natalimak1.narod.ru/dlk.htm

Вывод программы Белышева ortogon_u
Проверка ДЛК15 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 389318
Соквадратов:     0
Время в сек:     4320

20371 8124 2757 857 134 40 12 1

Программа прервана.

PS. Для удобства читателей и исследователей покажу квадрат Гергели в обычном виде

1 14 3 4 5 6 7 9 0 13 12 11 10 2 8
2 3 14 5 6 7 1 11 8 0 13 12 4 10 9
3 4 5 14 7 1 2 13 9 8 0 6 12 11 10
4 5 6 7 14 2 3 8 10 9 1 0 13 12 11
5 6 7 1 2 14 4 10 11 3 9 8 0 13 12
6 7 1 2 3 4 14 12 5 11 10 9 8 0 13
14 1 2 3 4 5 6 0 13 12 11 10 9 8 7
0 9 11 13 8 10 12 14 6 4 2 7 5 3 1
13 0 8 9 10 11 5 4 12 14 3 2 1 7 6
12 13 0 8 9 3 11 2 4 10 14 1 7 6 5
11 12 13 0 1 9 10 7 3 2 8 14 6 5 4
10 11 12 6 0 8 9 5 2 1 7 13 14 4 3
9 10 4 12 13 0 8 3 1 7 6 5 11 14 2
8 2 10 11 12 13 0 1 7 6 5 4 3 9 14
7 8 9 10 11 12 13 6 14 5 4 3 2 1 0

А это его КФ в формате 2
 0  8  9 14  7  3  4 10  5  2 13 12  6 11  1
 9  1  7  4  8 10  2 12  3 13 11  5 14  0  6
 4 14  2 13  9  1  7  8 11  0  6 10  3 12  5
 7  9  4  3  1  8 13 14 10 11  0  2  5  6 12
10  3  8  1  4 12  9  6  7 14  5  0 11  2 13
 8  7  1  9  3  5 14 13 12  4  2  6  0 10 11
13  2 11  0  5 14  6  4  9 12  7  1  8  3 10
14 13 12 11 10  9  8  7  6  5  4  3  2  1  0
 5 12  3 10  6  0 11  2  8  1  9 13  7 14  4
 2  4 13  7 14  6  0 11  1  9 12  8 10  5  3
 1 11  6 12 13  2  5  0  4  3 10 14  9  8  7
 3  5 10  8 12  7  1  9  0  6 14 11 13  4  2
 6  0 14  5 11 13  3  1  2 10  8  4 12  7  9
11 10  0  6  2  4 12  5 14  7  3  9  1 13  8
12  6  5  2  0 11 10  3 13  8  1  7  4  9 14

КФ получена канонизатором Harry White.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6518 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6519 - Posted: 4 Oct 2020, 17:37:58 UTC
Last modified: 4 Oct 2020, 17:40:34 UTC

Для порядка 26 ортогональная пара в теме есть, а вот SODLS нет.
Построила его программой Harry White

 0 17 20 16 19 10 21  5  4 12 11  1 25  2  3 14 13 24  6  7  9 23 15 18  8 22
11  1 16 19 15 18  0 20  6  5 12  2 24  3  4 13 23  7  8 10 22 25 17  9 21 14
12 11  2 15 18 25 17  1 19  7  6  3 23  4  5 22  8  9  0 21 24 16 10 20 14 13
 7 12 11  3 25 17 24 16  2 18  8  4 22  5  6  9 10  1 20 23 15  0 19 14 13 21
 9  8 12 11  4 24 16 23 15  3 17  5 21  6  7  0  2 19 22 25  1 18 14 13 20 10
16 10  9 12 11  5 23 15 22 25  4  6 20  7  8  3 18 21 24  2 17 14 13 19  0  1
 5 15  0 10 12 11  6 22 25 21 24  7 19  8  9 17 20 23  3 16 14 13 18  1  2  4
23  6 25  1  0 12 11  7 21 24 20  8 18  9 10 19 22  4 15 14 13 17  2  3  5 16
19 22  7 24  2  1 12 11  8 20 23  9 17 10  0 21  5 25 14 13 16  3  4  6 15 18
22 18 21  8 23  3  2 12 11  9 19 10 16  0  1  6 24 14 13 15  4  5  7 25 17 20
18 21 17 20  9 22  4  3 12 11 10  0 15  1  2 23 14 13 25  5  6  8 24 16 19  7
 3  4  5  6  7  8  9 10  0  1  2 11 13 14 12 25 15 16 17 18 19 20 21 22 23 24
24 23 22 21 20 19 18 17 16 15 25 14 12 11 13  2  1  0 10  9  8  7  6  5  4  3
25 24 23 22 21 20 19 18 17 16 15 12 14 13 11  1  0 10  9  8  7  6  5  4  3  2
 4  5  6  7  8  9 10  0  1  2  3 13 11 12 14 24 25 15 16 17 18 19 20 21 22 23
17  7 18  4 22 16  3  6 13 14  1 23  5 20 21 15 11 12 19 24  0  9 25  2 10  8
 6 19  3 23 17  2  5 13 14  0 18 24  4 21 22  7 16 11 12 20 25 10  8 15  1  9
20  2 24 18  1  4 13 14 10 19  5 25  3 22 23  8  6 17 11 12 21 15  9  7 16  0
 1 25 19  0  3 13 14  9 20  4 21 15  2 23 24 10  7  5 18 11 12 22 16  8  6 17
15 20 10  2 13 14  8 21  3 22  0 16  1 24 25 18  9  6  4 19 11 12 23 17  7  5
21  9  1 13 14  7 22  2 23 10 16 17  0 25 15  4 19  8  5  3 20 11 12 24 18  6
 8  0 13 14  6 23  1 24  9 17 22 18 10 15 16  5  3 20  7  4  2 21 11 12 25 19
10 13 14  5 24  0 25  8 18 23  7 19  9 16 17 20  4  2 21  6  3  1 22 11 12 15
13 14  4 25 10 15  7 19 24  6  9 20  8 17 18 16 21  3  1 22  5  2  0 23 11 12
14  3 15  9 16  6 20 25  5  8 13 21  7 18 19 12 17 22  2  0 23  4  1 10 24 11
 2 16  8 17  5 21 15  4  7 13 14 22  6 19 20 11 12 18 23  1 10 24  3  0  9 25

DSODLS этот ДЛК не является.

Порядок 26 относится к серии n=4k+2, поэтому ассоциативных ДЛК данного порядка не существует.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6519 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6520 - Posted: 4 Oct 2020, 17:44:31 UTC
Last modified: 4 Oct 2020, 17:52:26 UTC

Для порядка 27 копирую ортогональную пару, показанную в теме выше

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20
6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8
12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2
15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5
18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11
24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14
13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0
16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3
10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6
22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9
25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12
19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15
4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18
7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21
1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24
26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13
20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16
23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10
8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22
2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25
5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19
17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4
11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7
14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26
4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18
8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22
12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2
16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3
11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7
24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14
19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15
23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10
22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0 13 14 12 16 17 15 10 11 9
26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4 17 15 16 11 9 10 14 12 13
18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17
7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12 25 26 24 19 20 18 22 23 21
2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16 20 18 19 23 21 22 26 24 25
3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11 21 22 23 24 25 26 18 19 20
10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24 1 2 0 4 5 3 7 8 6
14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19 5 3 4 8 6 7 2 0 1
15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23 6 7 8 0 1 2 3 4 5
17 15 16 11 9 10 14 12 13 26 24 25 20 18 19 23 21 22 8 6 7 2 0 1 5 3 4
9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 0 1 2 3 4 5 6 7 8
13 14 12 16 17 15 10 11 9 22 23 21 25 26 24 19 20 18 4 5 3 7 8 6 1 2 0
20 18 19 23 21 22 26 24 25 2 0 1 5 3 4 8 6 7 11 9 10 14 12 13 17 15 16
21 22 23 24 25 26 18 19 20 3 4 5 6 7 8 0 1 2 12 13 14 15 16 17 9 10 11
25 26 24 19 20 18 22 23 21 7 8 6 1 2 0 4 5 3 16 17 15 10 11 9 13 14 12
5 3 4 8 6 7 2 0 1 14 12 13 17 15 16 11 9 10 23 21 22 26 24 25 20 18 19
6 7 8 0 1 2 3 4 5 15 16 17 9 10 11 12 13 14 24 25 26 18 19 20 21 22 23
1 2 0 4 5 3 7 8 6 10 11 9 13 14 12 16 17 15 19 20 18 22 23 21 25 26 24

Оба ДЛК ассоциативные и являются SODLS.
А значит, они должны быть и DSODLS согласно моей гипотезе.
Сейчас проверю.

Да! Эти ДЛК являются DSODLS.
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6520 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Profile Natalia Makarova
Project scientist
Avatar

Send message
Joined: 6 Apr 17
Posts: 14338
Credit: 0
RAC: 0
Message 6521 - Posted: 4 Oct 2020, 17:58:58 UTC

Здесь
https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5786
показана ортогональная пара ДЛК 28-го порядка, построенная методом составных квадратов.
Проверка этих ДЛК утилитой Harry White
Order? 28

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt

Counts
------
         2 diagonal Latin
         1 weakly pandiagonal
         2 center symmetric
         2 nfr
         1 orthogonal pair
         2 self-orthogonal

Отличные квадратики!
И согласно гипотезе они должны быть DSODLS.
Проверю завтра.
Сегодня был очень напряжённый день. Черепашке-то ничего, она работает себе спокойненько :)
А вот у меня был штурм... :)
My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg
ID: 6521 · Rating: 0 · rate: Rate + / Rate - Report as offensive     Reply Quote
Previous · 1 . . . 20 · 21 · 22 · 23 · 24 · 25 · 26 . . . 27 · Next

Message boards : Science : ОДЛК для порядков n>10


©2024 (C) Progger