ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 . . . 11 · 12 · 13 · 14 · 15 · 16 · 17 . . . 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А какое множество КФ ОДЛК получено в последней веточке! Вот результат проверки утилитой Harry White Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
90050 diagonal Latin
36513 associative
50466 axial symmetric
36258 double axial symmetric
90050 natural \diagonalУпиваюсь квадратами, как Пушкин гармонией :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Показываю 10 первых и 10 последних линеек из найденных на данный момент 515 линеек для СН ДЛК 12-го порядка 1 0 3 2 5 4 7 6 9 8 11 10 1 0 3 2 5 4 7 6 9 10 11 8 1 0 3 2 5 4 7 6 10 11 8 9 1 0 3 2 5 4 7 6 10 11 9 8 1 0 3 2 5 4 7 8 6 10 11 9 1 0 3 2 5 4 7 8 9 10 11 6 1 0 3 2 5 4 7 8 10 6 11 9 1 0 3 2 5 4 7 8 10 11 6 9 1 0 3 2 5 4 7 8 10 11 9 6 1 0 3 2 5 4 8 9 10 11 6 7 . . . . . 1 2 3 4 8 9 11 5 10 6 0 7 1 2 3 4 8 10 11 0 7 5 6 9 1 2 3 4 8 10 11 5 7 0 6 9 1 2 3 4 8 10 11 9 0 5 6 7 1 2 3 4 8 10 11 9 7 0 6 5 1 2 3 4 9 8 11 5 10 0 6 7 1 2 3 4 9 10 11 5 0 7 6 8 1 2 3 4 10 7 11 6 0 5 9 8 1 2 3 4 10 9 11 5 0 6 7 8 1 2 3 9 5 7 4 11 0 8 6 10 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Проверилось 326 ДЛК из 360. Отлично! Завтра добью эту ветку, если, конечно, не все оставшиеся 34 квадрата долгоиграющие. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Добивать ветку решила по три квадратика, потому что уже самый первый квадрат долгоиграющий Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 6128 Соквадратов: 8617 Время в сек: 5880 169 59 40 16 2 1 Вот три квадрата проверятся, потом ещё три запущу. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Для первого квадрата близится финиш Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 6128 Соквадратов: 12421 Время в сек: 8920 21 3 17 12 1 1 1 1 1 1 1 Посмотрим на следующий квадрат - будет ли таким же долгоиграющим. Ну, если таким же, ещё не страшно, только бы не более долгоиграющим. Поехал второй квадрат Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 7076 Соквадратов: 31945 Время в сек: 9370 492 35 28 3 5 1 1 1 1 1 Да, он оказался ещё более долгоиграющим, судя по количеству Д-трансверсалей. Ладно, покручу. Теперь у меня всего три квадратика запущено в проверку, управлюсь за день. Зато и ортогональных соквадратов будет много; может быть, найдутся ещё новые линейки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пошла проверка третьего квадрата Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 6028 Соквадратов: 31599 Время в сек: 30365 408 122 33 2 1 1 1 2 1 Полегче первых двух квадратов, побыстрее проверится. Кстати, заметка для Белышева, если он смотрит тему. Строка вывода соквадратов однозначно не очищается при переходе к следующему квадрату. Можно подумать, что соквадраты просто суммируются для всех проверяемых квадратов, но и это не так. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот и финиш Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 6028 Соквадратов: 12380 Время в сек: 36995 1 2 15 2 1 3 1 1 1 2 1 Для выхода нажмите любую клавишу: Посмотрите на проверенные квадратики [DLK(12953):1] 0 1 2 3 4 5 6 7 8 9 A B 2 B 6 4 A 8 3 1 7 5 0 9 9 0 1 7 5 3 8 6 4 A B 2 5 2 0 A 3 7 4 8 1 B 9 6 8 A 4 B 2 6 5 9 0 7 1 3 A 4 B 5 8 9 2 3 6 0 7 1 6 9 8 1 B 4 7 0 A 3 2 5 B 6 9 8 7 A 1 4 3 2 5 0 1 7 3 6 0 2 9 B 5 8 4 A 4 3 5 2 1 0 B A 9 6 8 7 7 8 A 9 6 B 0 5 2 1 3 4 3 5 7 0 9 1 A 2 B 4 6 8 [DLK(59607):12954] 0 1 2 3 4 5 6 7 8 9 A B 9 B 6 7 1 3 8 A 4 5 0 2 2 0 1 4 6 8 3 5 7 A B 9 5 7 8 A B 2 9 0 1 3 4 6 8 6 4 B 2 A 1 9 0 7 5 3 A 4 0 5 3 9 2 8 6 B 7 1 6 9 3 1 0 4 7 B A 8 2 5 B A 9 8 7 6 5 4 3 2 1 0 1 2 B 6 8 7 4 3 5 0 9 A 7 3 5 9 A B 0 1 2 6 8 4 4 8 A 2 5 0 B 6 9 1 3 7 3 5 7 0 9 1 A 2 B 4 6 8 [DLK(12380):72561] 0 1 2 3 4 5 6 7 8 9 A B 9 B 6 4 A 3 8 1 7 5 0 2 2 3 1 7 5 B 0 6 4 A 8 9 6 2 3 A B 7 4 0 1 8 9 5 8 6 4 B 2 A 1 9 0 7 5 3 5 4 B 1 3 9 2 8 A 0 7 6 1 9 8 5 0 4 7 B 6 3 2 A B A 9 8 7 6 5 4 3 2 1 0 A 7 0 6 8 2 9 3 5 B 4 1 7 0 5 2 1 8 3 A 9 6 B 4 4 8 A 9 6 0 B 5 2 1 3 7 3 5 7 0 9 1 A 2 B 4 6 8 С количеством соквадратов тут непонятки. Если у первого ДЛК 12953 соквадрата, что похоже на правду, то что такое 59607 у второго ДЛК? Сейчас посмотрю на mates. Тэк-с, всего ортогональных ДЛК от трёх квадратов найдено 84940. Похоже, что второй ДЛК дал рекорд ортогональных соквадратов! У меня было раньше максимальное количество ортогональных диагональных соквадратов от ДЛК 12-го порядка 41644, это от ДЛК, построенного Черновым. Итак, проверенные три квадрата дали 12953+59607+12380=84940 ортогональных диагональных соквадратов. Сейчас канонизирую и найду линейки, которым принадлежат КФ ОДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот что имеем File name? inp Format, (1 or 2)? 2 .. writing DLS to file output12CF2_8.txt number of DLS 84940 CFs 42727 elapsed time 0:02:27 42727 КФ ОДЛК! Они находятся в 227 линейках Order? 12 File? inp Input file is inp.txt .. writing squares to file inpDiags_4.txt Which \ 1 or / 2? 2 squares 42727 diags 227 Осталось проверить, найдены ли новые линейки. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Есть! Order? 12 File? inp Input file is inp.txt .. writing squares to file inpDiags_5.txt Which \ 1 or / 2? 2 squares 144308 diags 538 Все найденные КФ ОДЛК (а их уже 144308) дали 538 уникальных побочных диагоналей. Итак, добавилось 23 новые линейки, их стало 538. Думаю, что это ещё не окончательное решение для количества линеек. Новая нижняя граница, R(12)>=538. А я эту ветку буду добивать, у меня ещё 31 квадрат остался для проверки. Но это уже завтра. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот квадратик, давший рекордное количество (на данный момент) ортогональных диагональных соквадратов - 59607 0 1 2 3 4 5 6 7 8 9 A B 9 B 6 7 1 3 8 A 4 5 0 2 2 0 1 4 6 8 3 5 7 A B 9 5 7 8 A B 2 9 0 1 3 4 6 8 6 4 B 2 A 1 9 0 7 5 3 A 4 0 5 3 9 2 8 6 B 7 1 6 9 3 1 0 4 7 B A 8 2 5 B A 9 8 7 6 5 4 3 2 1 0 1 2 B 6 8 7 4 3 5 0 9 A 7 3 5 9 A B 0 1 2 6 8 4 4 8 A 2 5 0 B 6 9 1 3 7 3 5 7 0 9 1 A 2 B 4 6 8 Грандиозно!!! Утилита Harry White сообщает об этом ДЛК, представленном в формате 2 Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt
Counts
------
1 diagonal Latin
1 associative
1 double axial symmetric
1 natural \diagonalДважды симметричный по Гергели/Брауну и ассоциативный. У нас есть новая нижняя граница для члена a(12) последовательности OEIS A287695 a(12)>=59607. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу иллюстрации. Это ДЛК 12-го порядка, построенный Черновым 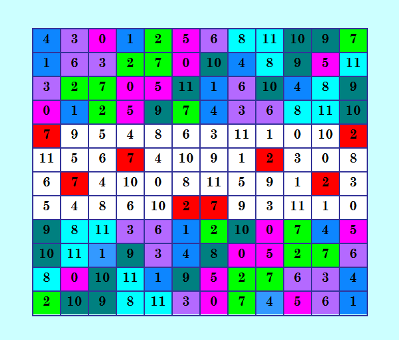 Симпатичный квадратик, частично ассоциативный и частично симметричный по Гергели/Брауну. Этот ДЛК имеет 41644 ортогональных диагональных соквадратов. Этот ДЛК построен мной  ДЛК ассоциативный (что показано раскраской) и дважды симметричный по Гергели/Брауну (и горизонтальная, и вертикальная симметрия). У этого ДЛК 59607 ортогональных диагональных соквадратов! А у ДЛК 10-го порядка у нас пока только 10 ортогональных диагональных соквадратов найдено от одного ДЛК. Да, порядок 10 какой-то совершенно особенный. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Интересно, нашёл Tomas Brada Top 10 CF-ODLK with most orthogonal mates: отсюда https://boinc.tbrada.eu/forum_thread.php?id=3104&postid=4149 А у меня Топ-10 для ОДЛК 12-го порядка собирается. 1. ДЛК, построенный методом Гергели 1 8 3 4 5 6 0 11 10 9 2 7 5 3 0 1 4 2 8 10 7 6 9 11 10 1 5 2 6 3 9 0 8 11 7 4 2 4 1 6 9 5 11 3 0 7 10 8 6 5 4 3 2 7 1 8 9 10 11 0 3 6 2 11 1 4 10 7 5 8 0 9 0 11 10 9 8 1 7 2 3 4 5 6 8 10 7 0 3 11 5 9 6 1 4 2 9 0 8 5 7 10 4 1 11 2 6 3 11 9 6 7 10 8 2 4 1 0 3 5 7 2 9 10 11 0 6 5 4 3 8 1 4 7 11 8 0 9 3 6 2 5 1 10 Д-трансверсалей: 5718 ОДЛК: 2199 КФ ОДЛК: 733 2. ДЛК, построенный Черновым 4 3 0 1 2 5 6 8 11 10 9 7 1 6 3 2 7 0 10 4 8 9 5 11 3 2 7 0 5 11 1 6 10 4 8 9 0 1 2 5 9 7 4 3 6 8 11 10 7 9 5 4 8 6 3 11 1 0 10 2 11 5 6 7 4 10 9 1 2 3 0 8 6 7 4 10 0 8 11 5 9 1 2 3 5 4 8 6 10 2 7 9 3 11 1 0 9 8 11 3 6 1 2 10 0 7 4 5 10 11 1 9 3 4 8 0 5 2 7 6 8 0 10 11 1 9 5 2 7 6 3 4 2 10 9 8 11 3 0 7 4 5 6 1 Д-трансверсалей: 8760 ОДЛК: 41644 КФ ОДЛК: 10798 3. ДЛК, построенный мной 0 2 4 10 7 8 9 6 11 5 3 1 5 1 9 6 2 10 11 3 7 8 0 4 4 0 2 7 9 11 10 8 6 3 1 5 8 6 11 3 1 4 5 0 2 10 7 9 11 9 7 1 4 3 2 5 0 6 8 10 3 7 0 8 10 5 4 11 9 1 6 2 9 5 10 2 0 7 6 1 3 11 4 8 1 3 5 11 6 9 8 7 10 4 2 0 2 4 1 9 11 6 7 10 8 0 5 3 6 10 8 5 3 1 0 2 4 9 11 7 7 11 3 4 8 0 1 9 5 2 10 6 10 8 6 0 5 2 3 4 1 7 9 11 Д-трансверсалей: 7076 ОДЛК: 59607 КФ ОДЛК: ? (не канонизировала отдельно эти ОДЛК) Пока Топ-3 у меня для ОДЛК порядка 12. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Запущены в проверку на марьяжность ещё три квадрата (добиваю ветку). Это первый квадрат проверяется Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 3 Найдено ОДЛК: 0 Д-трансверсалей: 7168 Соквадратов: 53802 Время в сек: 17865 225 183 80 20 1 Возможно будет новый рекорд количества ОДЛК от одного ДЛК 12-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот и последовательность https://oeis.org/A309283 опубликована. Цитирую A309283 Number of equivalence classes of X-based filling of diagonals in a diagonal Latin square of order n. Однако странно: почему Ватутин не добавил член a(11)? Он ведь его посчитал, как сообщается здесь https://vk.com/wall162891802_1292 Мы с Harry White тоже посчитали количество линеек для СН ДЛК 11-го порядка. И не только посчитали. Я их все выписала, смотрите тут https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=6038 То есть нам известны 67 линеек для СН ДЛК 11-го порядка. С порядком 12 сложнее. На данный момент у меня есть только нижняя граница количества линеек для СН ДЛК 12-го порядка: a(12)>=538. КФ ОДЛК 12-го порядка слишком много, поэтому отдельные небольшие порции КФ ОДЛК не дают всех уникальных побочных диагоналей (линеек). PS. Я не утверждаю, что для СН ДЛК 11-го порядка существует 67 линеек. Наш результат получен эмпирически. Есть набор КФ ОДЛК, из этих КФ ОДЛК выписаны уникальные побочные диагонали, их оказалось 67. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Черепашка кричит: "Финиш!" :) Посмотрите на три проверенных сегодня квадратика [DLK(85439):1] 0 1 2 3 4 5 6 7 8 9 A B 9 B A 7 6 3 8 5 4 1 0 2 7 3 1 9 5 B 0 6 2 A 8 4 6 7 B A 3 2 9 8 1 0 4 5 B A 4 8 2 6 5 9 3 7 1 0 5 4 3 1 B 9 2 0 A 8 7 6 A 9 0 6 8 4 7 3 5 B 2 1 8 5 9 B 7 1 A 4 0 2 6 3 1 2 8 5 0 7 4 B 6 3 9 A 2 0 6 4 A 8 3 1 7 5 B 9 4 8 5 2 1 0 B A 9 6 3 7 3 6 7 0 9 A 1 2 B 4 5 8 [DLK(15004):85440] 0 1 2 3 4 5 6 7 8 9 A B 9 B A 4 5 8 3 6 7 1 0 2 2 3 1 7 6 0 B 5 4 A 8 9 6 2 B A 8 7 4 3 1 0 9 5 B A 4 8 2 6 5 9 3 7 1 0 5 4 0 1 3 9 2 8 A B 7 6 A 9 3 6 0 4 7 B 5 8 2 1 8 5 9 B 7 1 A 4 0 2 6 3 1 7 8 5 B 2 9 0 6 3 4 A 7 0 6 2 1 3 8 A 9 5 B 4 4 8 5 9 A B 0 1 2 6 3 7 3 6 7 0 9 A 1 2 B 4 5 8 [DLK(21):100444] 0 1 2 3 4 5 6 7 8 9 A B 4 B 5 9 3 1 A 8 2 6 0 7 B 3 1 7 5 2 9 6 4 A 8 0 7 8 9 A B 6 5 0 1 2 3 4 6 7 A 0 2 3 8 9 B 1 4 5 3 4 B 5 1 9 2 A 6 0 7 8 2 A 8 6 0 7 4 B 5 3 1 9 1 2 7 8 6 B 0 5 3 4 9 A A 0 6 4 9 8 3 2 7 5 B 1 5 9 3 B 7 A 1 4 0 8 2 6 9 5 0 1 8 4 7 3 A B 6 2 8 6 4 2 A 0 B 1 9 7 5 3 Есть рекорд! Первый квадрат имеет 85439 ортогональных диагональных соквадратов. Супер! Третий квадратик скромненький - очко :) У второго квадрата 15004 ОДЛК. Сейчас рассмотрю mates. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, от трёх квадратиков получено 100464 ОДЛК, которые дали 47010 КФ ОДЛК File name? inp Format, (1 or 2)? 2 .. writing DLS to file output12CF2_11.txt number of DLS 100464 CFs 47010 elapsed time 0:02:56 Эти КФ ОДЛК находятся в 236 линейках Order? 12 File? inp Input file is inp.txt .. writing squares to file inpDiags.txt Which \ 1 or / 2? 2 squares 47010 diags 236 Осталось проверить, найдены ли новые линейки. Есть! Order? 12 File? inp Input file is inp.txt .. writing squares to file inpDiags_1.txt Which \ 1 or / 2? 2 squares 191318 diags 553 Добавились 15 новых линеек, их стало 553. Интернсно, сколько же всего линеек для СН ДЛК 12-го порядка? Я думаю, Белышеву не понадобится грид, чтобы это посчитать. Он знает, как линейки образуются в КФ. Я этого не знаю. Поэтому мне нужны сами КФ, чтобы увидеть в них побочные диагонали (=линейки). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю собирать Топ-10 групп пар ОДЛК 12-го порядка; пока Топ-4. 4. Мой ДЛК 0 2 4 10 7 9 8 6 11 5 3 1 5 1 3 6 8 10 11 9 7 2 0 4 6 10 2 5 9 1 0 8 4 3 11 7 8 6 1 3 10 4 5 11 2 0 7 9 1 3 7 11 4 8 9 5 10 6 2 0 9 7 10 2 1 5 4 0 3 11 6 8 3 5 0 8 11 7 6 10 9 1 4 2 11 9 5 1 6 2 3 7 0 4 8 10 2 4 11 9 0 6 7 1 8 10 5 3 4 0 8 7 3 11 10 2 6 9 1 5 7 11 9 4 2 0 1 3 5 8 10 6 10 8 6 0 5 3 2 4 1 7 9 11 Д-трансверсалей: 7168 ОДЛК: 85439 Ой, посмотреть бы на все эти ортогональки! Они небось узорчатые :) Невообразимо! У одного ДЛК 85439 ортогональных диагональных соквадратов! А мы всё с двушками, с тройками и четвёрками возимся для ДЛК 10-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Заглянула на форум boinc.ru Давненько там не была. Вот что нашла https://boinc.ru/forum/topic/novosti-proekta-rakesearch/?part=6#postid-2042 Цитирую В тех приложениях, что сделал Даниэль, исходный код легко перекомпилируется для поиска квадратов с 11 по 16 порядка. Вот оригинальный текст с переводом: Улыбнулась! Автор сообщения, видимо, ничего не знает об этой теме, иначе бы он так не писал. Конечно, ортогональные ДЛК для порядков 11 - 16 существуют, причём в огромных количествах. И никакой разведки делать не надо. За 2 месяца найдётся столько ортогональных ДЛК, что БД лопнет :) Если один ДЛК 12-го порядка может дать 85439 ОДЛК, трудно представить, сколько ОДЛК могут дать 1000000 ДЛК данного порядка. Ну, собственно, эта тема и посвящена исследованию ОДЛК порядков n>10. Расскажите автору сообщения об этой теме, пусть заглянет :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю добивать ветку. Сегодня запустила проверку сразу 15 квадратов, есть скромненькие (мало ОДЛК имеют). А вот сейчас проверяется долгоиграющий квадрат Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 15 Найдено ОДЛК: 0 Д-трансверсалей: 7116 Соквадратов: 53934 Время в сек: 26545 44 156 30 12 4 1 Скоро финиш. Попадёт квадрат в Топ-10, хотя и не рекорд. Посмотрим, что там следом идёт. Если нет больше долгоиграющих, то быстро проверятся оставшиеся квадраты. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Закончилась проверка 15 квадратов. Этот долгоиграющий квадрат, оказывается, был последним [DLK(59855):295] 0 1 2 3 4 5 6 7 8 9 A B 8 B 7 5 1 2 9 A 6 4 0 3 5 7 1 9 B 3 8 0 2 A 4 6 3 0 4 A 6 9 2 5 1 7 B 8 9 6 B 4 3 A 1 8 7 0 5 2 A 4 6 0 2 8 3 9 B 5 7 1 6 8 A 2 0 4 7 B 9 1 3 5 B A 9 8 7 6 5 4 3 2 1 0 7 2 8 6 A B 0 1 5 3 9 4 1 3 5 B 9 7 4 2 0 6 8 A 4 9 3 1 5 0 B 6 A 8 2 7 2 5 0 7 8 1 A 3 4 B 6 9 59855 ОДЛК! Неплохо, пока на втором месте квадрат. Сейчас Топ-5 покажу, расположу их в порядке убывания количеств ОДЛК, то есть на первом месте рекордный квадрат. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger