ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 . . . 7 · 8 · 9 · 10 · 11 · 12 · 13 . . . 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ещё раз подведу итоги a(9) ≥ 323, a(10) ≥ 866, a(11) ≥ 4665, a(12) ≥ 8760, a(13) ≥ 131106, a(14) ≥ 364252, a(15) ≥ 389318. У меня пока всё. Начиная с порядка 16, программа Белышева ortogon_u не считает все диагональные трансверсали в ДЛК, так как их больше заложенного в программе максимума. Например, для ДЛК 16-го порядка, построенного методом Гергели, программа Белышева выдаёт Число диагональных трансверсалей ДЛК16: 1 A 3 4 5 6 7 8 0 F E D C B 2 9 C 3 2 1 8 7 6 5 D E F 0 9 A B 4 7 8 5 E 3 4 1 2 A 9 C B 6 D 0 F 6 5 0 7 2 1 4 3 B C 9 A F 8 D E 2 1 4 3 6 D 8 7 F 0 5 E B C 9 A 3 4 1 2 F 8 5 6 E D 0 7 A 9 C B 8 7 6 5 4 3 2 9 1 A B C D E F 0 5 6 7 8 1 2 B 4 C 3 A 9 0 F E D 0 F E D C B A 1 9 2 3 4 5 6 7 8 D E F 0 9 A 3 C 4 B 2 1 8 7 6 5 A 9 C B E 5 0 F 7 8 D 6 3 4 1 2 B C 9 A 7 0 D E 6 5 8 F 2 1 4 3 F 0 D 6 B C 9 A 2 1 4 3 E 5 8 7 E D 8 F A 9 C B 3 4 1 2 7 0 5 6 9 2 B C D E F 0 8 7 6 5 4 3 A 1 4 B A 9 0 F E D 5 6 7 8 1 2 3 C превышает максимум 2097152 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
ДЛК 13-го порядка I confirm that this square has 9840 d-transverses and my porogram found 45 orthogonal mates. It took just over two hours on my PC. First two are: 8 7 0 1 6 9 3 10 5 11 12 4 2 9 0 4 6 10 3 8 11 1 12 2 5 7 3 6 11 10 1 5 9 8 0 4 7 2 12 2 10 5 4 8 6 1 7 3 0 9 12 11 12 9 6 0 5 11 2 3 4 7 8 10 1 4 12 10 9 7 1 5 6 11 2 0 8 3 10 2 8 7 0 4 12 9 6 3 1 11 5 6 5 7 12 11 10 0 2 8 1 3 9 4 0 8 12 3 9 2 11 1 7 5 4 6 10 1 4 9 8 3 12 6 5 2 10 11 7 0 5 11 3 2 12 7 4 0 10 9 6 1 8 7 1 2 11 4 0 10 12 9 8 5 3 6 11 3 1 5 2 8 7 4 12 6 10 0 9 3 6 0 8 2 4 7 5 9 10 11 1 12 12 0 11 4 5 6 3 1 2 9 8 10 7 4 11 2 3 7 8 1 0 10 5 6 12 9 9 5 6 7 10 12 2 4 8 0 1 3 11 0 7 12 10 9 2 5 11 3 6 4 8 1 8 12 4 11 3 1 9 7 5 2 10 6 0 1 3 5 2 11 9 8 6 7 12 0 4 10 5 9 1 12 0 11 6 10 4 7 3 2 8 10 8 3 9 4 7 0 12 6 1 2 11 5 7 4 10 5 8 3 12 2 1 11 9 0 6 6 2 9 0 1 5 10 8 11 4 12 7 3 11 1 8 6 12 10 4 9 0 3 7 5 2 2 10 7 1 6 0 11 3 12 8 5 9 4 |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
Number of transversals. In my project, I have a DLK10 with 1212 transversals. But A287644 a(10) >= 5504 from Parker and Brown. width: 15 isLK isDLK 0 7 8 9 6 13 10 4 3 5 12 2 11 14 1 4 1 7 0 8 14 12 5 6 11 3 10 13 2 9 14 5 2 7 1 0 13 6 10 4 9 12 3 8 11 9 13 6 3 7 2 1 14 5 8 11 4 0 10 12 6 8 12 14 4 7 3 13 0 10 5 1 9 11 2 1 14 0 11 13 5 7 12 9 6 2 8 10 3 4 8 2 13 1 10 12 6 11 14 3 0 9 4 5 7 11 10 9 8 0 1 2 7 12 13 14 6 5 4 3 7 9 10 5 14 11 0 3 8 2 4 13 1 12 6 10 11 4 6 12 8 5 2 7 9 1 3 14 0 13 12 3 5 13 9 4 14 1 11 7 10 0 2 6 8 2 4 14 10 3 6 9 0 13 12 7 11 8 1 5 3 6 11 2 5 10 4 8 1 14 13 7 12 9 0 5 12 1 4 11 3 8 9 2 0 6 14 7 13 10 13 0 3 12 2 9 11 10 4 1 8 5 6 7 14 init_trans(15) used 753 nodes num_trans: 305408 time: <1s width: 16 isLK isDLK 0 7 8 6 9 10 13 14 5 3 4 2 15 12 11 1 5 1 7 8 6 9 12 13 15 4 3 14 11 10 2 0 4 15 2 7 8 6 11 12 14 5 13 10 0 3 1 9 12 5 14 3 7 8 10 11 13 15 0 1 4 2 9 6 1 11 15 13 4 7 0 10 12 14 2 5 3 9 6 8 3 2 10 14 12 5 1 0 11 13 15 4 9 6 8 7 10 0 1 2 3 4 6 9 7 8 11 12 13 14 15 5 11 10 0 1 2 3 8 7 9 6 12 13 14 15 5 4 13 12 11 10 0 1 9 6 8 7 14 15 5 4 3 2 2 3 4 5 15 14 7 8 6 9 1 0 10 11 12 13 7 8 6 9 11 0 14 15 4 2 10 3 1 5 13 12 8 6 9 12 10 13 15 5 3 1 7 11 2 0 4 14 6 9 13 11 14 15 5 4 2 0 8 7 12 1 10 3 9 14 12 15 5 2 4 3 1 10 6 8 7 13 0 11 15 13 5 4 1 12 3 2 0 11 9 6 8 7 14 10 14 4 3 0 13 11 2 1 10 12 5 9 6 8 7 15 init_trans(16) used 851 nodes num_trans: 1879316 time: 2.3s width: 17 isLK isDLK 0 8 9 10 12 15 13 6 5 2 4 7 3 11 16 14 1 3 1 8 0 9 11 14 12 6 5 16 4 10 15 13 2 7 6 4 2 8 1 0 10 13 7 15 5 9 14 12 3 16 11 14 7 5 3 8 2 1 9 16 6 0 13 11 4 15 10 12 7 13 16 6 4 8 3 2 15 1 12 10 5 14 9 11 0 2 16 12 15 7 5 8 4 14 11 9 6 13 0 10 1 3 10 3 15 11 14 16 6 8 13 0 7 12 1 9 2 4 5 1 9 4 14 10 13 15 7 12 16 11 2 0 3 5 6 8 12 11 10 9 0 1 2 3 8 13 14 15 16 7 6 5 4 8 10 11 13 16 14 5 0 4 9 1 3 6 2 12 7 15 11 12 14 7 15 4 9 16 3 8 10 0 2 5 1 13 6 13 15 6 16 3 10 7 5 2 12 8 11 9 1 4 0 14 16 5 7 2 11 6 4 15 1 14 13 8 12 10 0 3 9 4 6 1 12 5 3 16 10 0 7 15 14 8 13 11 9 2 5 0 13 4 2 7 11 1 9 3 6 16 15 8 14 12 10 9 14 3 1 6 12 0 11 10 4 2 5 7 16 8 15 13 15 2 0 5 13 9 12 14 11 10 3 1 4 6 7 8 16 init_trans(17) used 955 nodes num_trans: 12102527 time: 21.4s width: 18 isLK isDLK 0 4 7 10 8 9 1 11 3 12 2 6 13 15 17 5 14 16 17 1 5 7 10 8 9 0 4 11 3 12 14 16 6 13 15 2 11 16 2 6 7 10 8 1 5 0 4 13 15 17 12 14 3 9 12 0 15 3 17 7 10 2 6 1 5 14 16 11 13 4 9 8 13 11 1 14 4 16 7 3 17 2 6 15 0 12 5 9 8 10 14 12 0 2 13 5 15 4 16 3 17 1 11 6 9 8 10 7 2 13 11 1 3 12 6 5 15 4 16 0 17 9 8 10 7 14 16 15 14 13 12 11 0 7 10 8 9 17 6 5 4 3 2 1 5 6 17 16 15 14 13 9 8 10 7 4 3 2 1 0 11 12 4 5 6 17 16 15 14 10 7 9 8 3 2 1 0 11 12 13 6 17 16 15 14 13 12 8 9 7 10 5 4 3 2 1 0 11 3 7 10 8 9 0 17 12 2 13 1 11 5 14 16 6 4 15 7 10 8 9 11 6 16 13 1 14 0 2 12 4 15 17 5 3 10 8 9 12 5 17 2 14 0 15 11 7 1 13 3 16 6 4 8 9 13 4 6 1 3 15 11 16 12 10 7 0 14 2 17 5 9 14 3 5 0 2 4 16 12 17 13 8 10 7 11 15 1 6 15 2 4 11 1 3 5 17 13 6 14 9 8 10 7 12 16 0 1 3 12 0 2 4 11 6 14 5 15 16 9 8 10 7 13 17 init_trans(18) used 1065 nodes num_trans: 82602438 time: 2m 57.4s |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
I confirm that this square has 9840 d-transverses and my porogram found 45 orthogonal mates. It took just over two hours on my PC. First two are: Это хороший результат. Ваша программа работает быстро. Справится ли ваша программа со следующим ДЛК 13-го порядка? 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 Здесь 131106 диагональных трансверсалей, как посчитала программа Белышева ortogon_u. Я думаю, что этот ДЛК 13-го порядка является претендентом на максимальное количество ортогональных ДЛК. То есть это нижняя граница для члена a(13) в последовательности OEIS https://oeis.org/A287695 Кстати, я нашла нижние границы для членов a(11) и a(12) a(11) ≥ 26914 a(12) ≥ 41644 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
In my project, I have a DLK10 with 1212 transversals. Вы имеете в виду диагональные трансверсали или общие трансверсали? В последовательности OEIS https://oeis.org/A287644 Maximum number of transversals in a diagonal Latin square of order n. рассматриваются общие трансверсали. ДЛК10 Брауна имеет 866 диагональных трансверсалей и 5504 общих трансверсалей. Смотрите здесь https://boinc.progger.info/odlk/forum_thread.php?id=162&postid=5894 Нам сейчас интересны диагональные трансверсали, так как мы занимаемся поиском ОДЛК. Если у вас есть ДЛК10, имеющий 1212 диагональных трансверсалей, покажите его, пожалуйста. Для ДЛК 10-го порядка это текущий максимум количества диагональных трансверсалей. Максимальные количества диагональных трансверсалей в ДЛК рассматриваются в последовательности https://oeis.org/A287648 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
width: 15 isLK isDLK Это не максимальное количество диагональных трансверсалей для ДЛК 15-го порядка. ДЛК15, построенный методом Гергели, имеет 389318 диагональных трансверсалей. width: 16 isLK isDLK Это не максимальное количество диагональных трансверсалей для ДЛК 16-го порядка. Вот что выдаёт программа Белышева для ДЛК16 Число диагональных трансверсалей ДЛК16: 1 A 3 4 5 6 7 8 0 F E D C B 2 9 C 3 2 1 8 7 6 5 D E F 0 9 A B 4 7 8 5 E 3 4 1 2 A 9 C B 6 D 0 F 6 5 0 7 2 1 4 3 B C 9 A F 8 D E 2 1 4 3 6 D 8 7 F 0 5 E B C 9 A 3 4 1 2 F 8 5 6 E D 0 7 A 9 C B 8 7 6 5 4 3 2 9 1 A B C D E F 0 5 6 7 8 1 2 B 4 C 3 A 9 0 F E D 0 F E D C B A 1 9 2 3 4 5 6 7 8 D E F 0 9 A 3 C 4 B 2 1 8 7 6 5 A 9 C B E 5 0 F 7 8 D 6 3 4 1 2 B C 9 A 7 0 D E 6 5 8 F 2 1 4 3 F 0 D 6 B C 9 A 2 1 4 3 E 5 8 7 E D 8 F A 9 C B 3 4 1 2 7 0 5 6 9 2 B C D E F 0 8 7 6 5 4 3 A 1 4 B A 9 0 F E D 5 6 7 8 1 2 3 C превышает максимум 2097152 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
width: 16 isLK isDLK 0 14 1 7 2 4 3 5 13 11 12 10 15 9 6 8 15 1 6 0 5 3 4 2 10 12 11 13 8 14 9 7 3 5 2 12 1 7 0 6 14 8 15 9 4 10 13 11 4 2 13 3 6 0 7 1 9 15 8 14 11 5 10 12 6 0 7 1 4 10 5 3 11 13 2 12 9 15 8 14 1 7 0 6 11 5 2 4 12 10 13 3 14 8 15 9 5 3 4 2 7 1 6 8 0 14 9 15 10 12 11 13 2 4 3 5 0 6 9 7 15 1 14 8 13 11 12 10 13 11 12 10 15 9 14 0 8 6 1 7 2 4 3 5 10 12 11 13 8 14 1 15 7 9 6 0 5 3 4 2 14 8 15 9 12 2 13 11 3 5 10 4 1 7 0 6 9 15 8 14 3 13 10 12 4 2 5 11 6 0 7 1 11 13 10 4 9 15 8 14 6 0 7 1 12 2 5 3 12 10 5 11 14 8 15 9 1 7 0 6 3 13 2 4 8 6 9 15 10 12 11 13 5 3 4 2 7 1 14 0 7 9 14 8 13 11 12 10 2 4 3 5 0 6 1 15 init_trans(16) used 851 nodes num_trans: 15456144 time: 10.5s |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
width: 19 isLK isDLK 0 9 1 6 8 7 3 5 4 17 18 14 13 15 11 10 12 2 16 2 1 9 8 7 6 5 4 3 16 13 18 14 10 15 11 0 12 17 1 0 2 9 6 8 4 3 5 15 14 13 18 11 10 7 17 16 12 6 8 7 3 9 4 0 2 1 14 12 17 16 18 5 13 15 11 10 8 7 6 5 4 9 2 1 0 13 16 12 17 3 18 14 10 15 11 7 6 8 4 3 5 9 0 2 12 17 16 1 14 13 18 11 10 15 3 5 4 0 2 1 6 9 7 11 15 8 10 12 17 16 18 14 13 5 4 3 2 1 0 8 7 9 10 6 15 11 16 12 17 13 18 14 9 3 5 1 0 2 7 6 8 18 11 10 15 17 16 12 14 13 4 18 17 16 15 14 13 12 11 10 9 5 1 6 2 7 3 8 4 0 14 15 13 17 18 16 11 12 6 1 10 9 8 0 4 2 3 7 5 13 14 15 16 17 18 10 8 12 6 1 11 9 4 2 0 7 5 3 15 13 14 18 16 17 1 10 11 2 8 6 12 9 0 4 5 3 7 11 12 10 14 15 3 17 18 16 7 0 4 2 13 9 5 6 1 8 10 11 12 13 5 15 16 17 18 3 4 2 0 7 14 9 1 8 6 12 10 11 7 13 14 18 16 17 8 2 0 4 5 3 15 9 6 1 17 18 0 11 12 10 14 15 13 4 3 7 5 6 1 8 16 9 2 16 2 18 10 11 12 13 14 15 0 7 5 3 1 8 6 4 17 9 4 16 17 12 10 11 15 13 14 5 9 3 7 8 6 1 2 0 18 init_trans(19) used 1181 nodes num_trans: 631935677 time: 20m 35.8s |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
width: 16 isLK isDLK 0 14 1 7 2 4 3 5 13 11 12 10 15 9 6 8 15 1 6 0 5 3 4 2 10 12 11 13 8 14 9 7 3 5 2 12 1 7 0 6 14 8 15 9 4 10 13 11 4 2 13 3 6 0 7 1 9 15 8 14 11 5 10 12 6 0 7 1 4 10 5 3 11 13 2 12 9 15 8 14 1 7 0 6 11 5 2 4 12 10 13 3 14 8 15 9 5 3 4 2 7 1 6 8 0 14 9 15 10 12 11 13 2 4 3 5 0 6 9 7 15 1 14 8 13 11 12 10 13 11 12 10 15 9 14 0 8 6 1 7 2 4 3 5 10 12 11 13 8 14 1 15 7 9 6 0 5 3 4 2 14 8 15 9 12 2 13 11 3 5 10 4 1 7 0 6 9 15 8 14 3 13 10 12 4 2 5 11 6 0 7 1 11 13 10 4 9 15 8 14 6 0 7 1 12 2 5 3 12 10 5 11 14 8 15 9 1 7 0 6 3 13 2 4 8 6 9 15 10 12 11 13 5 3 4 2 7 1 14 0 7 9 14 8 13 11 12 10 2 4 3 5 0 6 1 15 init_trans(16) used 851 nodes num_trans: 15456144 time: 10.5s Грандиозно! Можно считать, что a(16)>=15456144. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
In my project, I have a DLK10 with 1212 transversals. After checking my notes, those are unfortunately general transverses. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У меня есть набор ДЛК10 из последней постобработки (более миллиона ДЛК). Когда работала программа Белышева ortogon_u для этого набора, там мелькали большие количества диагональных трансверсалей. Я видела наибольшее - 994 Д-трансверсалей. Но не могу найти ДЛК с таким количеством Д-трансверсалей. Tomas вы можете посчитать количество Д-трансверсалей во всех ДЛК этого набора и выбрать максимальное количество? При этом важно установить сам ДЛК с максимальным количеством Д-трансверсалей. Набор ДЛК я вам пришлю. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата У меня есть набор ДЛК10 из последней постобработки (более миллиона ДЛК). Показываю скриншот; работает программа Белышева ortogon_u, это постобработка одним из моих алгоритмов 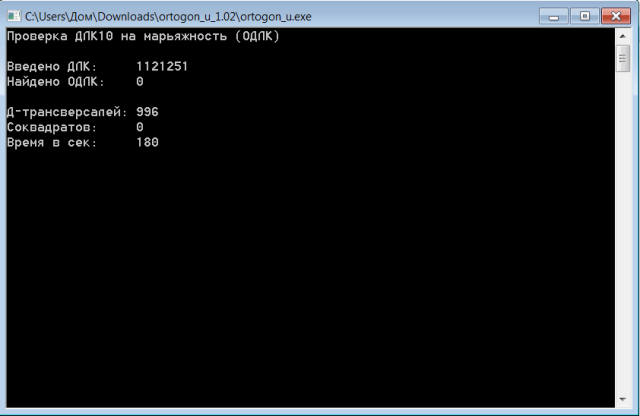 Здесь видим 996 Д-трансверсалей. Но установить ДЛК с таким количеством Д-трансверсалей никак не могу :( Кроме того, у меня закрадывается сомнение: есть ли такой ДЛК вообще? Корректен ли здесь вывод количества Д-трансверсалей? Не происходит ли наложение количеств Д-трансверсалей при такой массовой обработке ДЛК? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Пробежалась по порядкам от n=91 до n=100. Обнаружила всего два проблемных порядка: 93 и 94. Для порядка 94 одиночный ДЛК строится методом Гергели по моей программке, показанной выше (k=47). Для порядка 93 пытаюсь построить одиночный ДЛК методом Линдера по программе Чернова. Пока ничего не получается. Вот, например, сейчас работает программа Microsoft Windows [Version 6.1.7601] (c) Корпорация Майкрософт (Microsoft Corp.), 2009. Все права защищены. C:\Users\Дом>cd C:\Users\Дом\Downloads\test_dols_2 C:\Users\Дом\Downloads\test_dols_2>test 4 1 24 >d93.txt Ошибок не выдала, вроде работает, но сколько она будет думать и придумает ли в конце концов чего-нибудь - одному Богу известно. Порядок квадрата Q большой - 24. Найти подходящий квадрат довольно сложно. Вот и задумалась программа. В методе Гергели должен построиться одиночный ДЛК 93-го порядка, надо смотреть порядки данной серии. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Нет, не выруливает программа Чернова на ДЛК 93-го порядка. Если бы разобраться, как из квадрата Q получается квадрат P1, можно вручную попробовать построить. Только технические сложности опять же будут: слишком большой квадрат. Ладно пока оставляю этот одиночный ДЛК. Итак, до порядка n=100 почти все одиночные ДЛК для проблемных порядков у нас имеются. Для некоторых проблемных порядков и ортогональные пары построены. Теперь надо закрывать белые пятна. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Полная система MOLS 13-го порядка №1 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 0 2 3 4 5 6 7 8 9 10 11 12 0 1 3 4 5 6 7 8 9 10 11 12 0 1 2 4 5 6 7 8 9 10 11 12 0 1 2 3 5 6 7 8 9 10 11 12 0 1 2 3 4 6 7 8 9 10 11 12 0 1 2 3 4 5 7 8 9 10 11 12 0 1 2 3 4 5 6 8 9 10 11 12 0 1 2 3 4 5 6 7 9 10 11 12 0 1 2 3 4 5 6 7 8 10 11 12 0 1 2 3 4 5 6 7 8 9 11 12 0 1 2 3 4 5 6 7 8 9 10 12 0 1 2 3 4 5 6 7 8 9 10 11 №2 0 1 2 3 4 5 6 7 8 9 10 11 12 2 3 4 5 6 7 8 9 10 11 12 0 1 4 5 6 7 8 9 10 11 12 0 1 2 3 6 7 8 9 10 11 12 0 1 2 3 4 5 8 9 10 11 12 0 1 2 3 4 5 6 7 10 11 12 0 1 2 3 4 5 6 7 8 9 12 0 1 2 3 4 5 6 7 8 9 10 11 1 2 3 4 5 6 7 8 9 10 11 12 0 3 4 5 6 7 8 9 10 11 12 0 1 2 5 6 7 8 9 10 11 12 0 1 2 3 4 7 8 9 10 11 12 0 1 2 3 4 5 6 9 10 11 12 0 1 2 3 4 5 6 7 8 11 12 0 1 2 3 4 5 6 7 8 9 10 №3 0 1 2 3 4 5 6 7 8 9 10 11 12 3 4 5 6 7 8 9 10 11 12 0 1 2 6 7 8 9 10 11 12 0 1 2 3 4 5 9 10 11 12 0 1 2 3 4 5 6 7 8 12 0 1 2 3 4 5 6 7 8 9 10 11 2 3 4 5 6 7 8 9 10 11 12 0 1 5 6 7 8 9 10 11 12 0 1 2 3 4 8 9 10 11 12 0 1 2 3 4 5 6 7 11 12 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 11 12 0 4 5 6 7 8 9 10 11 12 0 1 2 3 7 8 9 10 11 12 0 1 2 3 4 5 6 10 11 12 0 1 2 3 4 5 6 7 8 9 №4 0 1 2 3 4 5 6 7 8 9 10 11 12 4 5 6 7 8 9 10 11 12 0 1 2 3 8 9 10 11 12 0 1 2 3 4 5 6 7 12 0 1 2 3 4 5 6 7 8 9 10 11 3 4 5 6 7 8 9 10 11 12 0 1 2 7 8 9 10 11 12 0 1 2 3 4 5 6 11 12 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 11 12 0 1 6 7 8 9 10 11 12 0 1 2 3 4 5 10 11 12 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 11 12 0 5 6 7 8 9 10 11 12 0 1 2 3 4 9 10 11 12 0 1 2 3 4 5 6 7 8 №5 0 1 2 3 4 5 6 7 8 9 10 11 12 5 6 7 8 9 10 11 12 0 1 2 3 4 10 11 12 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 11 12 0 1 7 8 9 10 11 12 0 1 2 3 4 5 6 12 0 1 2 3 4 5 6 7 8 9 10 11 4 5 6 7 8 9 10 11 12 0 1 2 3 9 10 11 12 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 11 12 0 6 7 8 9 10 11 12 0 1 2 3 4 5 11 12 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 11 12 0 1 2 8 9 10 11 12 0 1 2 3 4 5 6 7 №6 0 1 2 3 4 5 6 7 8 9 10 11 12 6 7 8 9 10 11 12 0 1 2 3 4 5 12 0 1 2 3 4 5 6 7 8 9 10 11 5 6 7 8 9 10 11 12 0 1 2 3 4 11 12 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 11 12 0 1 2 3 10 11 12 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 11 12 0 1 2 9 10 11 12 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 11 12 0 1 8 9 10 11 12 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 11 12 0 7 8 9 10 11 12 0 1 2 3 4 5 6 №7 0 1 2 3 4 5 6 7 8 9 10 11 12 7 8 9 10 11 12 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 11 12 0 8 9 10 11 12 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 11 12 0 1 9 10 11 12 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 11 12 0 1 2 10 11 12 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 11 12 0 1 2 3 11 12 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 11 12 0 1 2 3 4 12 0 1 2 3 4 5 6 7 8 9 10 11 6 7 8 9 10 11 12 0 1 2 3 4 5 №8 0 1 2 3 4 5 6 7 8 9 10 11 12 8 9 10 11 12 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 11 12 0 1 2 11 12 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 11 12 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 11 12 0 9 10 11 12 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 11 12 0 1 2 3 12 0 1 2 3 4 5 6 7 8 9 10 11 7 8 9 10 11 12 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 11 12 0 1 10 11 12 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 11 12 0 1 2 3 4 №9 0 1 2 3 4 5 6 7 8 9 10 11 12 9 10 11 12 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 11 12 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 11 12 0 10 11 12 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 11 12 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 11 12 0 1 11 12 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 11 12 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 11 12 0 1 2 12 0 1 2 3 4 5 6 7 8 9 10 11 8 9 10 11 12 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 11 12 0 1 2 3 №10 0 1 2 3 4 5 6 7 8 9 10 11 12 10 11 12 0 1 2 3 4 5 6 7 8 9 7 8 9 10 11 12 0 1 2 3 4 5 6 4 5 6 7 8 9 10 11 12 0 1 2 3 1 2 3 4 5 6 7 8 9 10 11 12 0 11 12 0 1 2 3 4 5 6 7 8 9 10 8 9 10 11 12 0 1 2 3 4 5 6 7 5 6 7 8 9 10 11 12 0 1 2 3 4 2 3 4 5 6 7 8 9 10 11 12 0 1 12 0 1 2 3 4 5 6 7 8 9 10 11 9 10 11 12 0 1 2 3 4 5 6 7 8 6 7 8 9 10 11 12 0 1 2 3 4 5 3 4 5 6 7 8 9 10 11 12 0 1 2 №11 0 1 2 3 4 5 6 7 8 9 10 11 12 11 12 0 1 2 3 4 5 6 7 8 9 10 9 10 11 12 0 1 2 3 4 5 6 7 8 7 8 9 10 11 12 0 1 2 3 4 5 6 5 6 7 8 9 10 11 12 0 1 2 3 4 3 4 5 6 7 8 9 10 11 12 0 1 2 1 2 3 4 5 6 7 8 9 10 11 12 0 12 0 1 2 3 4 5 6 7 8 9 10 11 10 11 12 0 1 2 3 4 5 6 7 8 9 8 9 10 11 12 0 1 2 3 4 5 6 7 6 7 8 9 10 11 12 0 1 2 3 4 5 4 5 6 7 8 9 10 11 12 0 1 2 3 2 3 4 5 6 7 8 9 10 11 12 0 1 №12 0 1 2 3 4 5 6 7 8 9 10 11 12 12 0 1 2 3 4 5 6 7 8 9 10 11 11 12 0 1 2 3 4 5 6 7 8 9 10 10 11 12 0 1 2 3 4 5 6 7 8 9 9 10 11 12 0 1 2 3 4 5 6 7 8 8 9 10 11 12 0 1 2 3 4 5 6 7 7 8 9 10 11 12 0 1 2 3 4 5 6 6 7 8 9 10 11 12 0 1 2 3 4 5 5 6 7 8 9 10 11 12 0 1 2 3 4 4 5 6 7 8 9 10 11 12 0 1 2 3 3 4 5 6 7 8 9 10 11 12 0 1 2 2 3 4 5 6 7 8 9 10 11 12 0 1 1 2 3 4 5 6 7 8 9 10 11 12 0 В этой системе только два ЛК не являются ДЛК - №1 и №12. Таким образом, мы имеем ещё и систему MODLS 13-го порядка, состоящую из 10 взаимно ортогональных ДЛК. Я построила эту систему вручную методом циклического сдвига. Все ЛК и ДЛК в этой системе получаются друг из друга перестановкой строк. Аналогично можно построить полную систему MOLS любого порядка n>3, являющегося простым числом. И точно так же в такой системе будет содержаться система MODLS данного порядка, содержащая n-3 взаимно ортогональных ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Интересны результаты проверки полной системы MOLS 13-го порядка утилитой Harry White Order? 13
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
2 Latin
10 diagonal Latin
10 pandiagonal
12 center symmetric
12 nfr
1 nfc
1 nfr nfc
1 self-transpose
11 orthogonal pair
10 self-orthogonalMy new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
I created a program to compress any size diagonal latin square, similar to namechdlk10. Of course, needs de-compressor too. Example: DrdVfwmF2ghiNUw45W9NmZr4iDgJwV49 0 1 2 3 4 5 6 7 8 9 10 11 3 6 1 4 11 2 9 0 7 10 5 8 1 4 11 2 5 8 3 6 9 0 7 10 2 3 4 5 10 11 0 1 6 7 8 9 11 10 5 0 7 6 1 8 3 2 9 4 8 5 6 11 0 9 10 3 4 1 2 7 6 11 0 9 2 7 8 5 10 3 4 1 5 0 7 6 9 4 11 10 1 8 3 2 10 7 8 1 6 3 4 9 2 11 0 5 9 8 3 10 1 0 7 2 5 4 11 6 7 2 9 8 3 10 5 4 11 6 1 0 4 9 10 7 8 1 2 11 0 5 6 3 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Tomas вы можете сделать программу конвертирования такого ДЛК 5 8 3 7 9 6 4 0 1 A B 2 A 0 6 8 B 2 1 9 7 4 5 3 B 3 4 9 A 7 5 2 8 0 1 6 4 6 B 2 7 1 8 A 3 5 9 0 6 9 0 1 8 5 3 B 2 7 4 A 0 7 9 5 3 B A 1 6 2 8 4 8 A 7 3 0 9 6 4 5 B 2 1 1 2 A B 6 4 7 3 9 8 0 5 2 B 5 4 1 3 0 7 A 9 6 8 9 4 8 0 5 A 2 6 B 1 3 7 3 1 2 A 4 8 9 5 0 6 7 B 7 5 1 6 2 0 B 8 4 3 A 9 в такой ДЛК 5 8 3 7 9 6 4 0 1 10 11 2 10 0 6 8 11 2 1 9 7 4 5 3 11 3 4 9 10 7 5 2 8 0 1 6 4 6 11 2 7 1 8 10 3 5 9 0 6 9 0 1 8 5 3 11 2 7 4 10 0 7 9 5 3 11 10 1 6 2 8 4 8 10 7 3 0 9 6 4 5 11 2 1 1 2 10 11 6 4 7 3 9 8 0 5 2 11 5 4 1 3 0 7 10 9 6 8 9 4 8 0 5 10 2 6 11 1 3 7 3 1 2 10 4 8 9 5 0 6 7 11 7 5 1 6 2 0 11 8 4 3 10 9 ??? Мне надо конвертировать 41644 ДЛК 12-го порядка. Я делаю это в Word, но Word не берёт большие массивы, поэтому делаю это порциями. Это очень нудно и долго. Желательно сделать программу для любого порядка n>10. Для дальнейшего использования конвертированных ДЛК в Бейсике мне нужно, чтобы между квадратами не было пустых строк. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот конвертировала уже 10200 ДЛК (из 41644) и проверила утилитой Harry White Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
10200 diagonal LatinОртогональных пар пока не обнаружено в этом множестве ДЛК. Мне интересно: будет ли в этом множестве ДЛК хотя бы одна ортогональная пара. Если будет, значит, нашлась тройка MODLS 12-го порядка. Напомню: исследуемое множество ДЛК - это ортогональные ДЛК к ДЛК, построенному Черновым 4 3 0 1 2 5 6 8 11 10 9 7 1 6 3 2 7 0 10 4 8 9 5 11 3 2 7 0 5 11 1 6 10 4 8 9 0 1 2 5 9 7 4 3 6 8 11 10 7 9 5 4 8 6 3 11 1 0 10 2 11 5 6 7 4 10 9 1 2 3 0 8 6 7 4 10 0 8 11 5 9 1 2 3 5 4 8 6 10 2 7 9 3 11 1 0 9 8 11 3 6 1 2 10 0 7 4 5 10 11 1 9 3 4 8 0 5 2 7 6 8 0 10 11 1 9 5 2 7 6 3 4 2 10 9 8 11 3 0 7 4 5 6 1 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Господа! У меня для вас есть отличная задача. Надо построить одиночный ДЛК 93-го порядка (а, может, даже и ортогональную пару!) методом Линдера. Предлагаю такие вспомогательные квадраты для построения. V = 1 3 4 2 4 2 1 3 2 4 3 1 3 1 2 4 Q = 8 2 1 0 7 6 5 4 3 9 10 11 12 13 14 16 23 22 21 20 19 18 17 15 1 11 3 2 5 4 7 6 10 0 8 9 14 15 19 13 21 20 23 22 17 16 12 18 7 6 14 4 3 2 1 0 12 13 5 15 8 22 10 11 19 18 17 16 23 9 21 20 5 4 7 13 1 0 3 2 14 15 12 6 21 11 8 9 17 16 19 18 10 20 23 22 6 7 4 5 9 3 0 1 13 12 15 17 2 8 11 10 18 19 16 14 22 23 20 21 4 5 6 7 0 10 2 3 15 14 18 12 11 1 9 8 16 17 13 19 20 21 22 23 2 3 0 1 6 7 15 5 9 23 11 10 13 12 4 14 22 8 20 21 18 19 16 17 0 1 2 3 4 5 6 12 20 10 9 8 15 14 13 7 11 21 22 23 16 17 18 19 10 17 8 9 14 15 12 13 16 11 6 19 20 21 22 23 4 5 18 7 0 1 2 3 18 9 10 11 12 13 14 15 8 19 16 5 22 23 20 21 6 7 4 17 2 3 0 1 14 15 12 23 10 11 8 9 0 21 22 13 16 17 18 19 20 1 2 3 4 5 6 7 12 13 20 15 8 9 10 11 22 3 14 21 18 19 16 17 2 23 0 1 6 7 4 5 15 14 13 12 11 16 9 8 21 20 23 22 17 10 7 18 1 0 3 2 5 4 19 6 13 12 15 14 19 8 11 10 23 22 21 20 9 18 17 4 3 2 1 0 7 6 5 16 11 10 9 8 15 14 13 22 17 16 19 18 1 20 23 12 5 4 7 6 21 0 3 2 9 8 11 10 13 12 21 14 19 18 17 16 23 2 15 20 7 6 5 4 3 22 1 0 17 16 19 18 21 20 23 7 11 1 2 3 4 5 6 22 0 10 9 8 15 14 13 12 19 18 17 16 23 22 4 20 2 8 0 1 6 7 21 5 9 3 11 10 13 12 15 14 21 20 23 22 17 1 19 18 4 5 13 7 0 16 2 3 15 14 6 12 11 10 9 8 23 22 21 20 2 18 17 16 6 7 4 14 19 3 0 1 13 12 15 5 9 8 11 10 20 21 22 6 16 17 18 19 5 4 7 23 10 0 3 2 14 15 12 13 1 11 8 9 22 23 5 21 18 19 16 17 7 6 20 4 3 9 1 0 12 13 14 15 8 2 10 11 16 0 18 19 20 21 22 23 1 17 3 2 5 4 12 6 10 11 8 9 14 15 7 13 3 19 16 17 22 23 20 21 18 2 1 0 7 6 5 15 8 9 10 11 12 13 14 4 Квадрат Q - ДЛК 24-го порядка, постреонный мной в статье http://www.natalimak1.narod.ru/ddolk.htm Построение выполнено методом Пелегрино-Ланселотти, описанным в статье Чернова http://alex-black.ru/article.php?content=124 Построена даже ортогональная пара этим методом. Таким образом, квадрат Q имеет ортогональный диагональный соквадрат. Квадрат P имеет порядок 1 и состоит из одного элемента. P = 1 Важно понять, как из квадрата Q получить квадрат P1. Для этого надо читать статью Чернова http://alex-black.ru/article.php?content=125 либо первоисточник – статью о методе Линдера Charles C.Linder. Construction Of Doubly Diagonalized Orthogonal Latin Squares. 1972 (эта статья есть в Сети) Ну, и уже отмечала выше: здесь технические трудности, так как порядок квадрата 93 слишком большой и разместить его на стандартном мониторе проблематично. Наверное, можно с таким квадратом работать на большом мониторе. Не знаю, ни разу даже не видела большой монитор. Разве что на почте видела большой монитор, на котором постоянно бежит реклама. Дерзайте, господа! Вдруг у вас получится. Итак, задача-минимум: построить одиночный ДЛК 93-го порядка методом Линдера; задача-максимум: построить ортогональную пару ДЛК 93-го порядка тем же методом. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger