Solving squares with large number of transversals is hard.

Да, это верно.
Программа Белышева вообще отказывается работать, когда количество трансверсалей очень большое (превышает некоторый максимум).

У меня есть такая идея (возможно, не совсем правильная): нельзя ли ограничить количество трансверсалей, а не задействовать их сразу все?
Вот в программе Белышева заложен некоторый максимум количества трансверсалей; хорошо, пусть для трансверсалей, найденных до этого максимума, и поищутся ортогональные ДЛК. Так нельзя поискать?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

I fixed my program and verified that the DLK11 has right number of d-transversals and co-squares.
Then I tried a DLK13, but I could not find a good input square, can you give me an example?
Now I am checking DLK14 (this one), but the sparse matrix has over 5 million nodes, it is going to take a long time, I do not know how long.
One DLK16 has 1879316 transversals, which yields over 30 million nodes in sparse matrix and 116138 rows in the smallest column. Huge numbers.
I definitely can not do DLK 26, it has more transversals than fit in my computer memory, and even if it did fit, is would run for a century.
We can try to just count the number of transversals, to provide lower bound to the oeis sequence.

Вот, например, интересный ДЛК 20-го порядка



Программа Белышева ortogon_u сообщает для данного ДЛК

Число диагональных трансверсалей ДЛК20:

0 B 9 I H 6 5 E 3 C 1 A 8 J G 7 4 F 2 D
A 1 J 8 7 G F 4 D 2 B 0 I 9 6 H E 5 C 3
4 F 2 D B 0 J 8 7 G 5 E 3 C A 1 I 9 6 H
E 5 C 3 1 A 9 I H 6 F 4 D 2 0 B 8 J G 7
8 J 6 H 4 F D 2 1 A 9 I 7 G 5 E C 3 0 B
I 9 G 7 E 5 3 C B 0 J 8 H 6 F 4 2 D A 1
2 D A 1 8 J 6 H F 4 3 C B 0 9 I 7 G E 5
C 3 0 B I 9 G 7 5 E D 2 1 A J 8 H 6 4 F
G 7 4 F C 3 A 1 8 J H 6 5 E D 2 B 0 9 I
6 H E 5 2 D 0 B I 9 7 G F 4 3 C 1 A J 8
B 0 I 9 6 H E 5 C 3 A 1 J 8 7 G F 4 D 2
1 A 8 J G 7 4 F 2 D 0 B 9 I H 6 5 E 3 C
F 4 D 2 0 B 8 J G 7 E 5 C 3 1 A 9 I H 6
5 E 3 C A 1 I 9 6 H 4 F 2 D B 0 J 8 7 G
J 8 H 6 F 4 2 D A 1 I 9 G 7 E 5 3 C B 0
9 I 7 G 5 E C 3 0 B 8 J 6 H 4 F D 2 1 A
D 2 1 A J 8 H 6 4 F C 3 0 B I 9 G 7 5 E
3 C B 0 9 I 7 G E 5 2 D A 1 8 J 6 H F 4
7 G F 4 3 C 1 A J 8 6 H E 5 2 D 0 B I 9
H 6 5 E D 2 B 0 9 I G 7 4 F C 3 A 1 8 J

превышает максимум 2097152

Максимум количества диагональных трансверсалей, заложенный в программе, равен 2097152.
Нельзя ли искать ортогональные ДЛК только для этого множества диагональных трансверсалей?

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

У меня есть такая идея (возможно, не совсем правильная): нельзя ли ограничить количество трансверсалей, а не задействовать их сразу все?
Вот в программе Белышева заложен некоторый максимум количества трансверсалей; хорошо, пусть для трансверсалей, найденных до этого максимума, и поищутся ортогональные ДЛК. Так нельзя поискать?
Нельзя ли искать ортогональные ДЛК только для этого множества диагональных трансверсалей?

Yes. This is possible. But it will most likely not find a solution.
There are actually two ways:

1) find all transversals, build the sparse matrix, and then limit how far the algorithm backtracks.
This has a good chance of finding a solution.

2) terminate the transversal search after X transversals found, but proceed next step as normal.
This has smaller chance of finding a solution, but avoids running out of memory.

Then I tried a DLK13, but I could not find a good input square, can you give me an example?

ДЛК 13-го порядка

0 12 11 7 10 4 8 2 3 5 6 9 1 
3 1 12 0 8 11 9 4 6 7 10 2 5 
5 4 2 12 1 9 10 7 8 11 3 6 0 
8 6 5 3 12 2 11 9 0 4 7 1 10 
10 9 7 6 4 12 0 1 5 8 2 11 3 
2 11 10 8 7 5 1 6 9 3 0 4 12 
1 2 3 4 5 6 12 0 11 10 9 8 7 
12 10 6 9 3 0 7 11 1 2 4 5 8 
9 5 8 2 11 7 6 12 10 0 1 3 4 
4 7 1 10 6 3 5 8 12 9 11 0 2 
6 0 9 5 2 1 4 3 7 12 8 10 11 
11 8 4 1 0 10 3 5 2 6 12 7 9 
7 3 0 11 9 8 2 10 4 1 5 12 6 

Я начинала проверку этого ДЛК программой Белышева ortogon_u

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 9840
Соквадратов:     5
Время в сек:     18195

641 257 8  28 5

Прервала программу, очень долго работает.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ещё пример ДЛК 13-го порядка (это из полной системы MOLS данного порядка)

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

Я начала проверку этого ДЛК программой Белышева

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 131106
Соквадратов:     4937
Время в сек:     10270

9114 4110 1558 230 24 16  6

Прервала программу.
В момент прерывания найдено 4949 ортогональных диагональных соквадратов. Я их сохранила.
Обратите внимание, сколько здесь диагональных трансверсалей.
Интересно бы узнать, сколько всего ортогональных диагональных соквадратов имеет этот ДЛК. Думаю, очень много.
Но проверить до конца здесь проблематично даже в 16 потоков.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Example for method 1 on DLK12.
In this one, there are 292 rows in the smallest column. Solving just first 10 of them gives the following distribution of solutions:

l(1) 1 / 292 r304 s2  
l(1) 2 / 292 r592 s0  
l(1) 3 / 292 r916 s6  
l(1) 4 / 292 r928 s144
l(1) 5 / 292 r940 s17  
l(1) 6 / 292 r1552 s10
l(1) 7 / 292 r1564 s13                    
l(1) 8 / 292 r1576 s16
l(1) 9 / 292 r1588 s10

(number of solutions is the last number)
Stopping after first solution is also possible.

Example for method 1 on DLK12.
In this one, there are 292 rows in the smallest column. Solving just first 10 of them gives the following distribution of solutions:

l(1) 1 / 292 r304 s2  
l(1) 2 / 292 r592 s0  
l(1) 3 / 292 r916 s6  
l(1) 4 / 292 r928 s144
l(1) 5 / 292 r940 s17  
l(1) 6 / 292 r1552 s10
l(1) 7 / 292 r1564 s13                    
l(1) 8 / 292 r1576 s16
l(1) 9 / 292 r1588 s10

(number of solutions is the last number)
Stopping after first solution is also possible.

Отлично!
Значит, моя идея реализуема.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

We can try to just count the number of transversals, to provide lower bound to the oeis sequence.

Когда-то давно видела эту последовательность OEIS (количество трансверсалей в ДЛК).
Пожалуйста, дайте ссылку.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Одиночный ДЛК 86-го порядка методом Гергели по своей программке построила и проверила утилитой Harry White

Order? 86

Enter the name of the squares file: inp1
.. writing type information to file inp1TypeDetail.txt

Counts
------
         1 diagonal Latin
         1 axial symmetric

Правильный ДЛК получился, утилита отметила у этого ДЛК симметричность по Гергели/Брауну.

О своей программке скажу несколько слов.
Вот скриншот из статьи
http://www.natalimak1.narod.ru/dlk.htm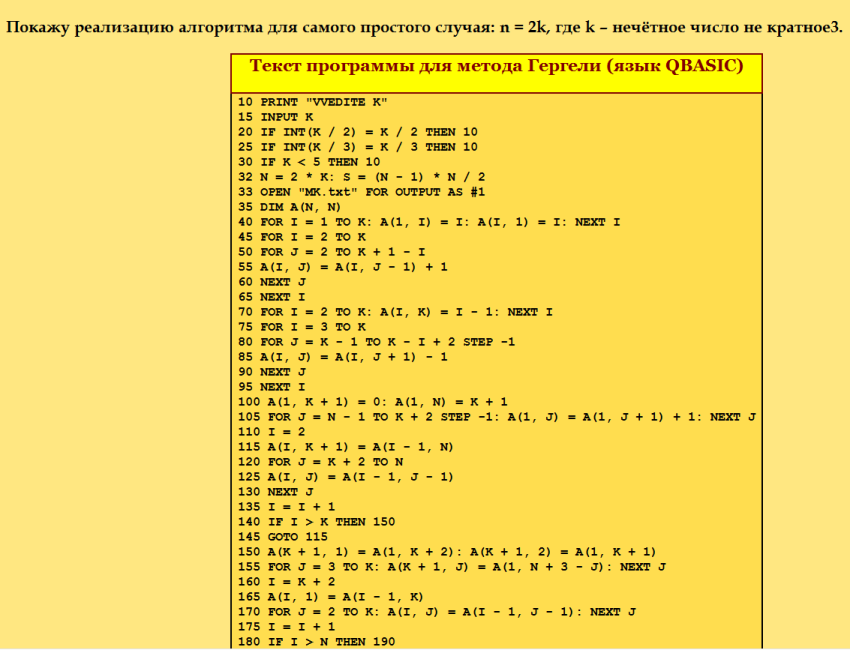



Тут не до конца, полный текст программы смотрите в указанной статье.

Не удивляйтесь :) Были такие времена, когда программы писались с номерами строк.
Возьмите текст программы, перепишите на любой язык, скомпилируйте.
Программа работает!
Я проверила для компилятора Бейсика, которым сейчас пользуюсь.
Программа запросит ввод значения k. Это всё, что ей нужно для построения ДЛК порядка n=2k.
Напомню: k нечётное число не кратное 3.

Пробуйте.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Stopping after first solution is also possible.

Вот как раз для ДЛК 26-го порядка мне нужен хотя бы один ортогональный ДЛК.
Напомню ДЛК

1 15 3 4 5 6 7 8 9 10 11 12 13 0 25 24 23 22 21 20 19 18 17 16 2 14 
2 3 17 5 6 7 8 9 10 11 12 13 1 14 0 25 24 23 22 21 20 19 18 4 16 15 
3 4 5 19 7 8 9 10 11 12 13 1 2 15 14 0 25 24 23 22 21 20 6 18 17 16 
4 5 6 7 21 9 10 11 12 13 1 2 3 16 15 14 0 25 24 23 22 8 20 19 18 17 
5 6 7 8 9 23 11 12 13 1 2 3 4 17 16 15 14 0 25 24 10 22 21 20 19 18 
6 7 8 9 10 11 25 13 1 2 3 4 5 18 17 16 15 14 0 12 24 23 22 21 20 19 
7 8 9 10 11 12 13 14 2 3 4 5 6 19 18 17 16 15 1 0 25 24 23 22 21 20 
8 9 10 11 12 13 1 2 16 4 5 6 7 20 19 18 17 3 15 14 0 25 24 23 22 21 
9 10 11 12 13 1 2 3 4 18 6 7 8 21 20 19 5 17 16 15 14 0 25 24 23 22 
10 11 12 13 1 2 3 4 5 6 20 8 9 22 21 7 19 18 17 16 15 14 0 25 24 23 
11 12 13 1 2 3 4 5 6 7 8 22 10 23 9 21 20 19 18 17 16 15 14 0 25 24 
12 13 1 2 3 4 5 6 7 8 9 10 24 11 23 22 21 20 19 18 17 16 15 14 0 25 
0 1 2 3 4 5 6 7 8 9 10 11 12 25 24 23 22 21 20 19 18 17 16 15 14 13 
25 0 14 15 16 17 18 19 20 21 22 23 11 24 10 9 8 7 6 5 4 3 2 1 13 12 
24 25 0 14 15 16 17 18 19 20 21 9 23 10 22 8 7 6 5 4 3 2 1 13 12 11 
23 24 25 0 14 15 16 17 18 19 7 21 22 9 8 20 6 5 4 3 2 1 13 12 11 10 
22 23 24 25 0 14 15 16 17 5 19 20 21 8 7 6 18 4 3 2 1 13 12 11 10 9 
21 22 23 24 25 0 14 15 3 17 18 19 20 7 6 5 4 16 2 1 13 12 11 10 9 8 
20 21 22 23 24 25 0 1 15 16 17 18 19 6 5 4 3 2 14 13 12 11 10 9 8 7 
19 20 21 22 23 24 12 0 14 15 16 17 18 5 4 3 2 1 13 25 11 10 9 8 7 6 
18 19 20 21 22 10 24 25 0 14 15 16 17 4 3 2 1 13 12 11 23 9 8 7 6 5 
17 18 19 20 8 22 23 24 25 0 14 15 16 3 2 1 13 12 11 10 9 21 7 6 5 4 
16 17 18 6 20 21 22 23 24 25 0 14 15 2 1 13 12 11 10 9 8 7 19 5 4 3 
15 16 4 18 19 20 21 22 23 24 25 0 14 1 13 12 11 10 9 8 7 6 5 17 3 2 
14 2 16 17 18 19 20 21 22 23 24 25 0 13 12 11 10 9 8 7 6 5 4 3 15 1 
13 14 15 16 17 18 19 20 21 22 23 24 25 12 11 10 9 8 7 6 5 4 3 2 1 0

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

We can try to just count the number of transversals, to provide lower bound to the oeis sequence.

Когда-то давно видела эту последовательность OEIS (количество трансверсалей в ДЛК).
Пожалуйста, дайте ссылку.

Нашла последовательность https://oeis.org/A287648

Maximum number of diagonal transversals in a diagonal Latin square of order n.

1, 0, 0, 4, 5, 6, 27, 120

Здесь, как я понимаю, приводятся максимальные значения количества диагональных трансверсалей в ДЛК до порядка n=8 включительно.
Ну, можно указать оценки (нижние границы) для следующих порядков.

Например, для ДЛК 9-го порядка имеем

Проверка ДЛК9 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 323
Соквадратов:     516
Время в сек:     5

Таким образом, a(9) ≥ 323.

Проверялся этот ДЛК из полной системы MOLS 9-го порядка

0 1 2 3 4 5 6 7 8
6 7 8 0 1 2 3 4 5
3 4 5 6 7 8 0 1 2
5 3 4 8 6 7 2 0 1
2 0 1 5 3 4 8 6 7
8 6 7 2 0 1 5 3 4
7 8 6 1 2 0 4 5 3
4 5 3 7 8 6 1 2 0
1 2 0 4 5 3 7 8 6

Данный ДЛК имеет максимальное известное на сегодня количество ортогональных диагональных соквадратов: 516.
Смотрите последовательность OEIS https://oeis.org/A287695

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для ДЛК 10-го порядка

Проверка ДЛК10 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 866
Соквадратов:     4
Время в сек:     5

Проверялся знаменитый ДЛК Брауна

0 8 5 1 7 3 4 6 9 2
5 1 7 2 9 8 0 3 4 6
1 7 2 9 5 6 8 0 3 4
9 6 4 3 0 2 7 1 5 8
3 0 8 6 4 1 5 9 2 7
4 3 0 8 6 5 9 2 7 1
7 2 9 5 1 4 6 8 0 3
6 4 3 0 8 9 2 7 1 5
2 9 6 4 3 7 1 5 8 0
8 5 1 7 2 0 3 4 6 9

Значит, a(10)>=866.
Мне кажется, я видела больше диагональных трансверсалей в ДЛК 10-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для ДЛК 11-го порядка

Проверка ДЛК11 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 4665
Соквадратов:     26914
Время в сек:     3535

1 83 24 8 4    1

Проверялся ДЛК из полной системы MOLS 11-го порядка

0 1 2 3 4 5 6 7 8 9 10
3 4 5 6 7 8 9 10 0 1 2
6 7 8 9 10 0 1 2 3 4 5
9 10 0 1 2 3 4 5 6 7 8
1 2 3 4 5 6 7 8 9 10 0
4 5 6 7 8 9 10 0 1 2 3
7 8 9 10 0 1 2 3 4 5 6
10 0 1 2 3 4 5 6 7 8 9
2 3 4 5 6 7 8 9 10 0 1
5 6 7 8 9 10 0 1 2 3 4
8 9 10 0 1 2 3 4 5 6 7

Таким образом, a(11)>=4665.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для ДЛК 12-го порядка

Проверка ДЛК12 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 8760
Соквадратов:     41644
Время в сек:     106380

1 4 19 4 4 9  3

Для выхода нажмите любую клавишу:

Проверялся ДЛК, построенный Черновым

4 3 0 1 2 5 6 8 11 10 9 7
1 6 3 2 7 0 10 4 8 9 5 11
3 2 7 0 5 11 1 6 10 4 8 9
0 1 2 5 9 7 4 3 6 8 11 10
7 9 5 4 8 6 3 11 1 0 10 2
11 5 6 7 4 10 9 1 2 3 0 8
6 7 4 10 0 8 11 5 9 1 2 3
5 4 8 6 10 2 7 9 3 11 1 0
9 8 11 3 6 1 2 10 0 7 4 5
10 11 1 9 3 4 8 0 5 2 7 6
8 0 10 11 1 9 5 2 7 6 3 4
2 10 9 8 11 3 0 7 4 5 6 1

Значит, a(12) ≥ 8760.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для ДЛК 13-го порядка

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 131106
Соквадратов:     4937
Время в сек:     10270

9114 4110 1558 230 24 16  6

Не проверено до конца, прервала программу.

Проверялся ДЛК из полной системы MOLS 13-го порядка

0 1 2 3 4 5 6 7 8 9 10 11 12
2 3 4 5 6 7 8 9 10 11 12 0 1
4 5 6 7 8 9 10 11 12 0 1 2 3
6 7 8 9 10 11 12 0 1 2 3 4 5
8 9 10 11 12 0 1 2 3 4 5 6 7
10 11 12 0 1 2 3 4 5 6 7 8 9
12 0 1 2 3 4 5 6 7 8 9 10 11
1 2 3 4 5 6 7 8 9 10 11 12 0
3 4 5 6 7 8 9 10 11 12 0 1 2
5 6 7 8 9 10 11 12 0 1 2 3 4
7 8 9 10 11 12 0 1 2 3 4 5 6
9 10 11 12 0 1 2 3 4 5 6 7 8
11 12 0 1 2 3 4 5 6 7 8 9 10

Таким образом, a(13) ≥ 131106.
Огромное количество трансверсалей!

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Подведу итоги
a(9) ≥ 323, a(10) ≥ 866, a(11) ≥ 4665, a(12) ≥ 8760, a(13) ≥ 131106

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Для ДЛК 14-го порядка

Проверка ДЛК14 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 364252
Соквадратов:     290
Время в сек:     43755

25632 10343 3872 1100 41 79 2   2

Не проверено до конца, прервала программу.

Проверялся ДЛК, постренный методом Гергели

1 9 3 4 5 6 7 0 13 12 11 10 2 8
2 3 11 5 6 7 1 8 0 13 12 4 10 9
3 4 5 13 7 1 2 9 8 0 6 12 11 10
4 5 6 7 8 2 3 10 9 1 0 13 12 11
5 6 7 1 2 10 4 11 3 9 8 0 13 12
6 7 1 2 3 4 12 5 11 10 9 8 0 13
0 1 2 3 4 5 6 13 12 11 10 9 8 7
13 0 8 9 10 11 5 12 4 3 2 1 7 6
12 13 0 8 9 3 11 4 10 2 1 7 6 5
11 12 13 0 1 9 10 3 2 8 7 6 5 4
10 11 12 6 0 8 9 2 1 7 13 5 4 3
9 10 4 12 13 0 8 1 7 6 5 11 3 2
8 2 10 11 12 13 0 7 6 5 4 3 9 1
7 8 9 10 11 12 13 6 5 4 3 2 1 0

Таким образом, a(14) ≥ 364252.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Выше я рассказала о группе MODLS 15-го порядка, состоящей из четырёх взаимно ортогональных ДЛК.
Группа построена мной на основе известной группы MOLS 15-го порядка.
Покажу эту группу, ДЛК преобразовала в традиционный формат

ОДЛК 1
0 6 11 9 8 2 14 7 1 13 10 3 12 4 5 
2 1 7 12 10 9 3 8 0 11 4 13 5 6 14 
1 3 2 8 13 11 10 9 12 5 0 6 7 14 4 
13 2 4 3 9 0 12 10 6 1 7 8 14 5 11 
7 0 3 5 4 10 1 11 2 8 9 14 6 12 13 
3 8 1 4 6 5 11 12 9 10 14 7 13 0 2 
10 4 9 2 5 7 6 13 11 14 8 0 1 3 12 
8 9 10 11 12 13 0 14 7 6 5 4 3 2 1 
5 10 8 7 1 14 4 6 13 0 12 9 2 11 3 
9 7 6 0 14 3 2 5 4 12 13 11 8 1 10 
6 5 13 14 2 1 9 4 8 3 11 12 10 7 0 
4 12 14 1 0 8 13 3 5 7 2 10 11 9 6 
11 14 0 13 7 12 5 2 3 4 6 1 9 10 8 
14 13 12 6 11 4 7 1 10 2 3 5 0 8 9 
12 11 5 10 3 6 8 0 14 9 1 2 4 13 7 

ОДЛК 2
0 10 7 2 5 11 8 13 6 1 9 4 14 12 3 
7 1 11 8 3 6 12 0 2 10 5 14 13 4 9 
3 8 2 12 9 4 7 1 11 6 14 0 5 10 13 
12 4 9 3 13 10 5 2 7 14 1 6 11 0 8 
8 13 5 10 4 0 11 3 14 2 7 12 1 9 6 
14 9 0 6 11 5 1 4 3 8 13 2 10 7 12 
4 14 10 1 7 12 6 5 9 0 3 11 8 13 2 
11 12 13 0 1 2 3 14 10 9 8 7 6 5 4 
9 6 1 4 10 7 2 12 13 5 0 8 3 14 11 
5 0 3 9 6 1 10 11 8 12 4 13 7 2 14 
13 2 8 5 0 9 14 10 4 7 11 3 12 6 1 
1 7 4 13 8 14 0 9 12 3 6 10 2 11 5 
6 3 12 7 14 13 4 8 0 11 2 5 9 1 10 
2 11 6 14 12 3 9 7 5 13 10 1 4 8 0 
10 5 14 11 2 8 13 6 1 4 12 9 0 3 7 

ОДЛК 3
0 8 6 12 2 1 11 4 7 14 3 13 10 5 9 
8 1 9 7 13 3 2 5 14 4 0 11 6 10 12 
14 9 2 10 8 0 4 6 5 1 12 7 11 13 3 
6 14 10 3 11 9 1 7 2 13 8 12 0 4 5 
3 7 14 11 4 12 10 8 0 9 13 1 5 6 2 
1 4 8 14 12 5 13 9 10 0 2 6 7 3 11 
11 2 5 9 14 13 6 10 1 3 7 8 4 12 0 
13 0 1 2 3 4 5 14 12 11 10 9 8 7 6 
7 5 11 1 0 10 8 3 13 6 14 2 12 9 4 
4 10 0 13 9 7 3 2 6 12 5 14 1 11 8 
9 13 12 8 6 2 7 1 3 5 11 4 14 0 10 
12 11 7 5 1 6 9 0 8 2 4 10 3 14 13 
10 6 4 0 5 8 12 13 11 7 1 3 9 2 14 
5 3 13 4 7 11 14 12 9 10 6 0 2 8 1 
2 12 3 6 10 14 0 11 4 8 9 5 13 1 7 

ОДЛК 4
0 5 12 6 11 4 7 2 8 9 14 1 3 10 13 
9 1 6 13 7 12 5 3 10 14 2 4 11 0 8 
11 10 2 7 0 8 13 4 14 3 5 12 1 9 6 
14 12 11 3 8 1 9 5 4 6 13 2 10 7 0 
5 14 13 12 4 9 2 6 7 0 3 11 8 1 10 
8 6 14 0 13 5 10 7 1 4 12 9 2 11 3 
2 9 7 14 1 0 6 8 5 13 10 3 12 4 11 
12 13 0 1 2 3 4 14 11 10 9 8 7 6 5 
4 11 5 10 3 6 12 1 13 7 8 14 0 2 9 
10 4 9 2 5 11 8 0 3 12 6 7 14 13 1 
3 8 1 4 10 7 0 13 9 2 11 5 6 14 12 
7 0 3 9 6 13 11 12 2 8 1 10 4 5 14 
13 2 8 5 12 10 14 11 6 1 7 0 9 3 4 
1 7 4 11 9 14 3 10 12 5 0 6 13 8 2 
6 3 10 8 14 2 1 9 0 11 4 13 5 12 7 

Посчитала количество диагональных трансверсалей у этих ОДЛК (программой Белышева ortogon_u); в порядке следования ОДЛК:
306605, 305868, 304818, 308292

У ДЛК 15-го порядка, построенного методом Гергели, 389318 диагональных трансверсалей.
Этот ДЛК показан выше.
Посмотрю, какие у меня ещё есть ДЛК 15-го порядка.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Вот ещё ортогональная пара 15-го порядка из статьи
http://www.natalimak1.narod.ru/dolk.htm
(построена по программе Чернова)

0 14 13 12 6 8 11 4 3 5 9 2 10 7 1 
4 1 14 0 13 7 9 5 6 10 3 11 8 2 12 
7 5 2 14 1 0 8 6 11 4 12 9 3 13 10 
12 8 6 3 14 2 1 7 5 13 10 4 0 11 9 
6 13 9 7 4 14 3 8 0 11 5 1 12 10 2 
1 7 0 10 8 5 14 9 12 6 2 13 11 3 4 
13 2 8 1 11 9 6 10 7 3 0 12 4 5 14 
10 11 12 13 0 1 2 14 9 8 7 6 5 4 3 
14 12 11 5 7 10 0 3 13 2 4 8 1 9 6 
11 10 4 6 9 13 5 2 14 12 1 3 7 0 8 
9 3 5 8 12 4 7 1 10 14 11 0 2 6 13 
2 4 7 11 3 6 12 0 8 9 14 10 13 1 5 
3 6 10 2 5 11 4 13 1 7 8 14 9 12 0 
5 9 1 4 10 3 13 12 2 0 6 7 14 8 11 
8 0 3 9 2 12 10 11 4 1 13 5 6 14 7 
 
0 13 14 11 10 4 8 12 6 3 1 7 5 9 2 
7 1 0 14 12 11 5 13 4 2 8 6 10 3 9 
5 8 2 1 14 13 12 0 3 9 7 11 4 10 6 
4 6 9 3 2 14 0 1 10 8 12 5 11 7 13 
11 5 7 10 4 3 14 2 9 13 6 12 8 0 1 
10 12 6 8 11 5 4 3 0 7 13 9 1 2 14 
1 11 13 7 9 12 6 4 8 0 10 2 3 14 5 
3 4 5 6 7 8 9 14 2 1 0 13 12 11 10 
12 14 10 9 3 7 1 11 13 5 2 0 6 4 8 
14 9 8 2 6 0 7 10 11 12 4 1 13 5 3 
8 7 1 5 13 6 2 9 14 10 11 3 0 12 4 
6 0 4 12 5 1 3 8 7 14 9 10 2 13 11 
13 3 11 4 0 2 10 7 5 6 14 8 9 1 12 
2 10 3 13 1 9 11 6 12 4 5 14 7 8 0 
9 2 12 0 8 10 13 5 1 11 3 4 14 6 7

Посчитала диагональные трансверсали у обоих ДЛК этой пары; их меньше, чем у ДЛК, построенного методом Гергели.

Так что, пока a(15)>=389318.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg