ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 . . . 4 · 5 · 6 · 7 · 8 · 9 · 10 . . . 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Что я пока поняла: квадрат V - это база. Обратите внимание на расположение раскрашенных подквадратов, они расположены точно по заданной квадратом V базе. С подквадратами пока не разбиралась, как они строятся. Есть совсем одинаковые подквадраты, а есть похожие, но несколько разные по своей структуре. Вот понять, как составлены все подквадраты, - не совсем просто только по примеру. Надо читать статью. Коллеги молчат. Написала Чернову и Беляеву. Нет, не интересуют их больше квадраты. Жаль! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Q = 1 3 2 5 6 4 3 2 4 6 1 5 5 6 3 1 4 2 2 5 6 4 3 1 6 4 1 2 5 3 4 1 5 3 2 6 Цитирую из статьи Чернова http://alex-black.ru/article.php?content=125 Аналогично с ортогональными квадратами. Если в дополнение к уже названным условиям взять по паре ортогональных квадратов V, Q, P1, получим пару ортогональных дважды диагональных латинских квадратов. Надежда рухнула: в примере для ДЛК 21-го порядка квадрат Q не имеет ортогонального соквадрата, так как это ЛК 6-го порядка. Таким образом, получается, что не для любого одиночного ДЛК, построенного методом Линдера, можно тем же методом построить ортогональный ему ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это вспомогательные квадраты, выданные программой Чернова при построении ДЛК 33-го порядка методом Линдера V = 1 3 4 5 7 8 6 2 3 2 6 7 8 5 1 4 2 6 3 8 1 4 5 7 5 1 8 4 3 7 2 6 8 4 7 6 5 2 3 1 4 7 5 1 2 6 8 3 6 8 1 2 4 3 7 5 7 5 2 3 6 1 4 8 Q = 1 3 2 5 4 4 2 5 1 3 5 4 3 2 1 3 5 1 4 2 2 1 4 3 5 P1 = 3 5 4 2 4 2 3 5 2 4 5 3 5 3 2 4 Здесь надежда есть: для всех трёх квадратов V, Q, P1 можно построить ортогональные квадраты. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Цитата Здесь надежда есть: для всех трёх квадратов V, Q, P1 можно построить ортогональные квадраты. Теоретически можно построить, однако ортогональный ДЛК к квадрату V программа Белышева ortogon_u не находит. Плохой квадрат V построился. И на ДЛК 33-го порядка надежда рухнула. Может быть, я что-то не так понимаю во всём этом. Конечно, есть ещё надежда найти ортогональный ДЛК к ДЛК Линдера другим методом. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Решила рассмотреть более простой пример в методе Линдера - для ДЛК 13-порядка. Покажу оба ДЛК, первый построен в статье Чернова, второй построен мной на основе ДЛК, построенного Черновым. 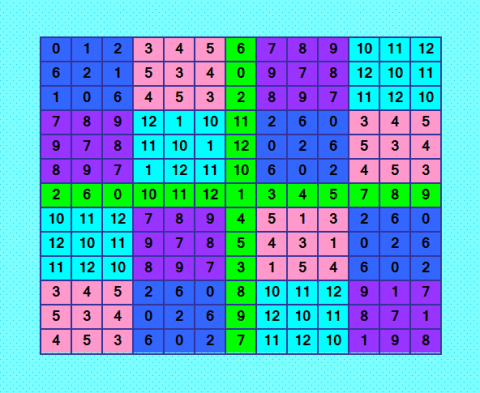 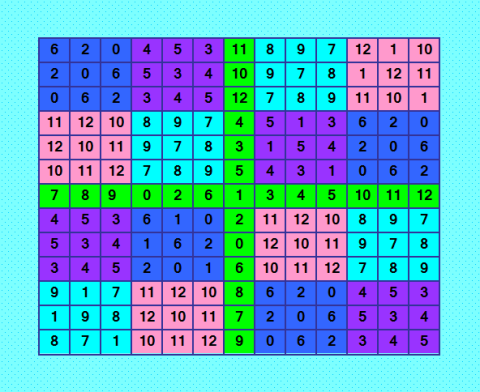 ДЛК у меня получился. Все вспомогательные квадраты (V, Q и P1) в этом примере хорошие, ортогональные соквадраты к ним легко строятся. Метод Линдера сильно похож на метод составных квадратов. Делала всё по своему опыту использования метода составных квадратов: на новую базу (ортогональную исходной) посадила ортогональные соквадраты для исходных подквадратов. База определяется квадратом V, по моему мнению. Оба ДЛК показаны раскрашенными, хорошо видны все подквадраты и база. Увы! Что-то я сделала не так, ортогональный ДЛК к ДЛК, построенному Черновым, у меня не получился. Вот вам супер-задача: найдите ошибку в моих построениях. Что я сделала не так? И как надо сделать правильно? PS. Есть у меня такая версия: подквадраты надо брать в том же порядке, как в исходном ДЛК. Попробую. Но сомневаюсь, что получится. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила построенный мной ДЛК на ортогональные соквадраты программой Белышева ortogonal_u, первый диагональный соквадрат нашёлся довольно быстро, дальше не стала искать, прервала программу. Вот какой ортогональный ДЛК нашёлся 0 8 1 9 A 3 2 5 B C 7 4 6 A 4 5 7 0 6 C 9 3 1 B 2 8 8 A B 4 7 C 6 1 2 0 9 5 3 3 C 0 8 6 A 1 B 9 5 4 7 2 5 B 6 2 9 4 8 7 0 A C 3 1 2 7 A 5 B 1 3 8 C 6 0 9 4 B 6 8 C 3 7 A 2 5 4 1 0 9 4 9 7 6 2 B 5 C 1 8 3 A 0 6 1 3 0 C 2 9 4 7 B 5 8 A 9 0 2 1 5 8 B A 4 3 6 C 7 C 5 4 A 8 9 0 3 6 7 2 1 B 1 3 9 B 4 5 7 0 A 2 8 6 C 7 2 C 3 1 0 4 6 8 9 A B 5 К ДЛК, построенному Черновым, тоже найден один ортогональный диагональный ДЛК, он показан выше. Следовательно, ДЛК 13-го порядка, построенные методом Линдера, не "пустышки". Однако методом Линдера построить ортогональную пару ДЛК данного порядка мне не удалось. Ну, и дальше двигаться не буду (для порядков 21 и 33), так как надо разобраться с примером для ДЛК 13-го порядка. Кто-нибудь когда-нибудь, возможно, разберётся. Я пока ничего не понимаю, все свои идеи применила, но ничего не получилось с ортогональной парой. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Попробовала расположить подквадраты в другом порядке, получила ещё один ДЛК 13-го порядка 6 2 0 11 12 10 8 4 5 3 9 1 7 2 0 6 12 10 11 7 5 3 4 1 9 8 0 6 2 10 11 12 9 3 4 5 8 7 1 8 9 7 4 5 3 11 12 1 10 6 2 0 9 7 8 5 3 4 10 1 12 11 2 0 6 7 8 9 3 4 5 12 11 10 1 0 6 2 3 4 5 0 2 6 1 10 11 12 7 8 9 11 12 10 6 1 0 2 8 9 7 4 5 3 12 10 11 1 6 2 0 9 7 8 5 3 4 10 11 12 2 0 1 6 7 8 9 3 4 5 5 1 3 8 9 7 4 6 2 0 11 12 10 1 5 4 9 7 8 3 2 0 6 12 10 11 4 3 1 7 8 9 5 0 6 2 10 11 12 Увы, как я и предполагала, ортогональный ДЛК к исходному ДЛК из статьи Чернова опять не получился. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Выше был показан ДЛК 33-го порядка, построенный методом Линдера. Показанный ДЛК был построен с применением командной строки test 8 1 5 Мне удалось построить ещё один ДЛК 33-го порядка методом Линдера, теперь с применением следующей командной строки test 4 1 9 Покажу вспомогательные квадраты, выданные программой в этом случае V = 1 3 4 2 4 2 1 3 2 4 3 1 3 1 2 4 Q = 1 3 2 5 4 7 6 9 8 3 2 1 6 7 8 9 4 5 2 1 3 7 6 9 8 5 4 5 6 8 4 9 1 2 3 7 4 7 9 8 5 2 1 6 3 7 4 5 9 8 6 3 1 2 9 8 4 1 3 5 7 2 6 6 9 7 3 2 4 5 8 1 8 5 6 2 1 3 4 7 9 P1 = 3 4 5 7 6 8 9 2 2 5 4 8 7 6 3 9 5 2 3 9 8 4 6 7 4 3 6 2 5 9 7 8 7 9 2 6 3 5 8 4 8 6 7 3 9 2 4 5 6 8 9 4 2 7 5 3 9 7 8 5 4 3 2 6 Построенный ДЛК 33-го порядка покажу далее раскрашенным. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ДЛК 33-го порядка, построенный методом Линдера по программе Чернова  Возможно ли построить ортогональный диагональный соквадрат к этому ДЛК методом Линдера, я не знаю. После неудачи с ортогональной парой ДЛК 13-го порядка, где все вспомогательные квадраты удобные, могу сказать, как сказал мудрец: "Я знаю только то, что ничего не знаю." My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Выше я приводила цитату с таблицей В таблице приводятся значения Q(n) для n от 2 до 499. Я приведу небольшой фрагмент этой таблицы (рис. 1). А теперь будем рассматривать группы MODLS, то есть группы взаимно ортогональных ДЛК. Обозначим QD(n) максимальное количество ОДЛК порядка n в группе MODLS. Для порядков 2, 3, 6 положим QD(n)=1, по аналогии с показанной таблицей для групп MOLS. [Для порядка n=3 не существует ортогональных ДЛК.] Имеем следующие известные значения QD(n) для групп MODLS порядков 2 - 20 (Ссылки на рисунки в моей статье ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin squares (MOLS) http://www.natalimak1.narod.ru/grolk.htm.) в первой колонке порядок квадрата, во второй колонке значение QD(n) n – QD(n) 2 – 1 3 – 1 (рис. 2) 4 – 2 (рис. 3) 5 – 2 (рис. 4) 6 – 1 7 – 4 (рис. 5) 8 – 6 (рис. 6) 9 – 6 (рис. 7) 10 – 2 (рис. 8 -10) 11 – 8 12 – ? 13 – 10 14 – ? 15 – 4 16 – 14 17 – 14 18 – ? 19 – 16 20 – ? Можно предположить, что QD(10)>2, QD(15)>4. Группу MODLS 15-го порядка, состоящую из четырёх взаимно ортогональных ДЛК я составила на основе известной группы MOLS данного порядка, о чём рассказано выше. Можно ли составить группу MODLS 15-го порядка, содержащую больше четырёх взаимно ортогональных ДЛК? Хороший вопрос! Ну, о порядке 10 мы всё уже хорошо знаем: пар ОДЛК огромное множество, тройку MODLS данного порядка пока не нашли (насколько мне известно). Даже и тройку MOLS не нашли. Для порядков 12, 14, 18 и 20, конечно, тоже можно предположить, что QD(n)>2. Однако пока мы имеем только ортогональны пары ДЛК для данных порядков. Вот хочу поискать группу MODLS 12-го порядка, содержащую больше двух взаимно ортогональных ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Напомню цитату из статьи New Bounds For Pairwise Orthogonal Diagonal Latin Squares Theorem 1.1 Как видим, для порядков 10, 12, 14, 15, 18 и 20 (указанные мной выше проблемные порядки) существование MODLS из пяти взаимно (попарно) ортогональных ДЛК не установлено. Ну, и дальше здесь перечислены проблемные порядки до порядка n=164. Может быть, на данный момент есть новости у математиков по этому вопросу. Убедительная просьба: кто обнаружит эти новости, сообщите, пожалуйста. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот для этого красивого ДЛК 12-го порядка из статьи Чернова 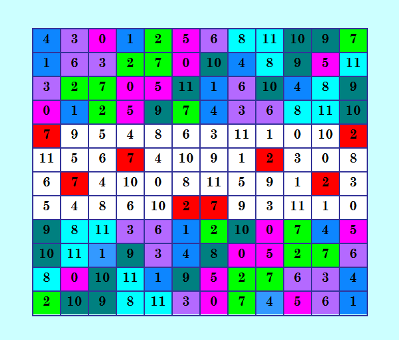 программа Белышева ortogonal_u нашла 41644 ортогональных диагональных соквадратов. Финал выполнения программы Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 8760 Соквадратов: 41644 Время в сек: 106380 1 4 19 4 4 9 3 Для выхода нажмите любую клавишу: В этой группе ОДЛК надо бы поискать группу MODLS 12-го порядка хотя бы из трёх взаимно ортогональных ДЛК. Неужели из такого огромного количества ОДЛК не найдётся хотя бы трёх взаимно ортогональных? Может, и не найдётся, чёрт их знает - эти квадраты :) У Паркера был ещё более крутой облом: он нашёл ЛК 10-го порядка, у которого более 12 миллионов ортогональных соквадратов, и... ни одной тройки MOLS! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Кстати, ссылка на мою тему "Латинские квадраты" на форуме dxdy.ru https://dxdy.ru/topic15897.html Тема была начата в те давние времена, когда я только начинала заниматься латинскими квадратами. А привело меня к этому занятию построение магических квадратов с помощью ортогональных латинских квадратов. Может быть, в этой теме начинающие найдут что-то полезное. Это сообщение https://boinc.progger.info/odlk/forum_thread.php?id=116&postid=3540 посмотрите. Там картинка как раз из темы "Латинские квадраты"  Сообщение Макса Алексеева о знаменитой статье Брауна и Ко о первых ортогональных парах ДЛК 10-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Никак не доберусь до проверки огромной группы ОДЛК 12-го порядка. Но у меня есть группа ОДЛК данного порядка поменьше. Эта группа ОДЛК получена от ДЛК, построенного методом Гергели, вот этого 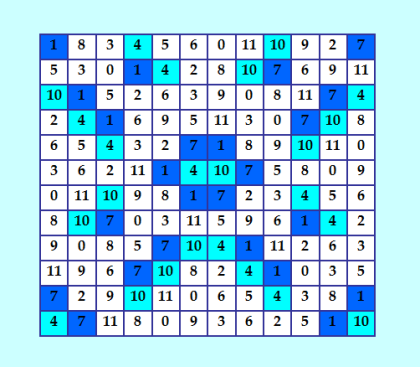 У этого ДЛК имеется 2199 ортогональных диагональных соквадратов. С этой группой можно поработать, она небольшая. Я уже нормализовала все ОДЛК, приготовилась к проверке. Покажу три первых нормализованных ОДЛК 0 1 2 3 4 5 6 7 8 9 10 11 10 9 0 8 7 6 5 4 3 11 2 1 11 2 8 1 6 7 4 5 10 3 9 0 9 5 3 4 10 0 11 1 7 8 6 2 2 11 6 10 3 4 7 8 1 5 0 9 8 7 5 9 1 11 0 10 2 6 4 3 3 10 7 5 11 9 2 0 6 4 1 8 4 3 1 11 5 2 9 6 0 10 8 7 7 8 9 6 0 1 10 11 5 2 3 4 6 0 10 7 9 3 8 2 4 1 11 5 5 4 11 2 8 10 1 3 9 0 7 6 1 6 4 0 2 8 3 9 11 7 5 10 0 1 2 3 4 5 6 7 8 9 10 11 10 9 0 8 7 6 5 4 3 11 2 1 11 2 8 1 6 4 7 5 10 3 9 0 9 5 3 7 10 0 11 1 4 8 6 2 2 11 6 10 3 7 4 8 1 5 0 9 8 4 5 9 1 11 0 10 2 6 7 3 3 10 7 5 11 9 2 0 6 4 1 8 7 3 1 11 5 2 9 6 0 10 8 4 4 8 9 6 0 1 10 11 5 2 3 7 6 0 10 4 9 3 8 2 7 1 11 5 5 7 11 2 8 10 1 3 9 0 4 6 1 6 4 0 2 8 3 9 11 7 5 10 0 1 2 3 4 5 6 7 8 9 10 11 10 8 7 5 0 2 9 11 6 4 3 1 2 3 11 6 10 4 7 1 5 0 8 9 1 2 6 7 8 0 11 3 4 5 9 10 11 5 8 10 9 7 4 2 1 3 6 0 9 6 3 4 11 1 10 0 7 8 5 2 8 10 4 0 6 9 2 5 11 7 1 3 7 0 10 2 5 8 3 6 9 1 11 4 4 9 0 8 1 6 5 10 3 11 2 7 5 11 1 9 7 3 8 4 2 10 0 6 3 7 5 1 2 11 0 9 10 6 4 8 6 4 9 11 3 10 1 8 0 2 7 5 Однако я сильно сомневаюсь, что в этой группе ОДЛК найдётся тройка MODLS. Ну а вдруг, чем чёрт не шутит :) Итак, что нужно проверить? Нужно проверить, есть ли в этой группе ОДЛК два ДЛК ортогональных друг другу. Не забываем: все эти ОДЛК ортогональны ДЛК, построенному методом Гергели. Задача предельно ясная, надо уже приступать к решению. Что-то я никак не раскачаюсь :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А между тем думаем о ДЛК и ОДЛК порядков n>50. И первый же порядок в этом диапазоне проблемный. Одиночный ДЛК 51-го порядка моментально построила программа Чернова, реализующая метод Линдера. Использованная командная строка test 10 1 6 >d51.txt ДЛК 51-го порядка, построенный методом Линдера 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 2 25 3 1 0 6 9 8 5 7 11 14 13 10 12 16 19 18 15 17 21 24 23 20 22 4 27 30 29 26 28 32 35 34 31 33 37 40 39 36 38 42 45 44 41 43 47 50 49 46 48 4 2 1 25 3 7 8 6 9 5 12 13 11 14 10 17 18 16 19 15 22 23 21 24 20 0 28 29 27 30 26 33 34 32 35 31 38 39 37 40 36 43 44 42 45 41 48 49 47 50 46 1 3 0 4 25 9 7 5 6 8 14 12 10 11 13 19 17 15 16 18 24 22 20 21 23 2 30 28 26 27 29 35 33 31 32 34 40 38 36 37 39 45 43 41 42 44 50 48 46 47 49 3 4 25 0 2 8 5 9 7 6 13 10 14 12 11 18 15 19 17 16 23 20 24 22 21 1 29 26 30 28 27 34 31 35 33 32 39 36 40 38 37 44 41 45 43 42 49 46 50 48 47 5 6 7 8 9 30 27 29 3 28 20 21 22 23 24 46 47 48 49 50 41 42 43 44 45 26 25 1 4 2 0 15 16 17 18 19 31 32 33 34 35 10 11 12 13 14 36 37 38 39 40 6 9 8 5 7 29 26 3 27 30 21 24 23 20 22 47 50 49 46 48 42 45 44 41 43 28 1 0 2 25 4 16 19 18 15 17 32 35 34 31 33 11 14 13 10 12 37 40 39 36 38 7 8 6 9 5 28 29 27 26 3 22 23 21 24 20 48 49 47 50 46 43 44 42 45 41 30 4 2 1 0 25 17 18 16 19 15 33 34 32 35 31 12 13 11 14 10 38 39 37 40 36 9 7 5 6 8 27 3 30 28 26 24 22 20 21 23 50 48 46 47 49 45 43 41 42 44 29 0 4 25 1 2 19 17 15 16 18 35 33 31 32 34 14 12 10 11 13 40 38 36 37 39 8 5 9 7 6 3 28 26 30 29 23 20 24 22 21 49 46 50 48 47 44 41 45 43 42 27 2 25 0 4 1 18 15 19 17 16 34 31 35 33 32 13 10 14 12 11 39 36 40 38 37 20 21 22 23 24 15 16 17 18 19 50 47 49 3 48 5 6 7 8 9 10 11 12 13 14 46 36 37 38 39 40 26 27 28 29 30 25 1 4 2 0 31 32 33 34 35 41 42 43 44 45 21 24 23 20 22 16 19 18 15 17 49 46 3 47 50 6 9 8 5 7 11 14 13 10 12 48 37 40 39 36 38 27 30 29 26 28 1 0 2 25 4 32 35 34 31 33 42 45 44 41 43 22 23 21 24 20 17 18 16 19 15 48 49 47 46 3 7 8 6 9 5 12 13 11 14 10 50 38 39 37 40 36 28 29 27 30 26 4 2 1 0 25 33 34 32 35 31 43 44 42 45 41 24 22 20 21 23 19 17 15 16 18 47 3 50 48 46 9 7 5 6 8 14 12 10 11 13 49 40 38 36 37 39 30 28 26 27 29 0 4 25 1 2 35 33 31 32 34 45 43 41 42 44 23 20 24 22 21 18 15 19 17 16 3 48 46 50 49 8 5 9 7 6 13 10 14 12 11 47 39 36 40 38 37 29 26 30 28 27 2 25 0 4 1 34 31 35 33 32 44 41 45 43 42 41 42 43 44 45 10 11 12 13 14 25 1 4 2 0 35 32 34 3 33 15 16 17 18 19 31 46 47 48 49 50 36 37 38 39 40 26 27 28 29 30 5 6 7 8 9 20 21 22 23 24 42 45 44 41 43 11 14 13 10 12 1 0 2 25 4 34 31 3 32 35 16 19 18 15 17 33 47 50 49 46 48 37 40 39 36 38 27 30 29 26 28 6 9 8 5 7 21 24 23 20 22 43 44 42 45 41 12 13 11 14 10 4 2 1 0 25 33 34 32 31 3 17 18 16 19 15 35 48 49 47 50 46 38 39 37 40 36 28 29 27 30 26 7 8 6 9 5 22 23 21 24 20 45 43 41 42 44 14 12 10 11 13 0 4 25 1 2 32 3 35 33 31 19 17 15 16 18 34 50 48 46 47 49 40 38 36 37 39 30 28 26 27 29 9 7 5 6 8 24 22 20 21 23 44 41 45 43 42 13 10 14 12 11 2 25 0 4 1 3 33 31 35 34 18 15 19 17 16 32 49 46 50 48 47 39 36 40 38 37 29 26 30 28 27 8 5 9 7 6 23 20 24 22 21 15 16 17 18 19 41 42 43 44 45 26 27 28 29 30 25 1 4 2 0 40 37 39 3 38 36 31 32 33 34 35 10 11 12 13 14 46 47 48 49 50 20 21 22 23 24 5 6 7 8 9 16 19 18 15 17 42 45 44 41 43 27 30 29 26 28 1 0 2 25 4 39 36 3 37 40 38 32 35 34 31 33 11 14 13 10 12 47 50 49 46 48 21 24 23 20 22 6 9 8 5 7 17 18 16 19 15 43 44 42 45 41 28 29 27 30 26 4 2 1 0 25 38 39 37 36 3 40 33 34 32 35 31 12 13 11 14 10 48 49 47 50 46 22 23 21 24 20 7 8 6 9 5 19 17 15 16 18 45 43 41 42 44 30 28 26 27 29 0 4 25 1 2 37 3 40 38 36 39 35 33 31 32 34 14 12 10 11 13 50 48 46 47 49 24 22 20 21 23 9 7 5 6 8 18 15 19 17 16 44 41 45 43 42 29 26 30 28 27 2 25 0 4 1 3 38 36 40 39 37 34 31 35 33 32 13 10 14 12 11 49 46 50 48 47 23 20 24 22 21 8 5 9 7 6 25 0 4 2 1 26 30 28 29 27 46 50 48 49 47 31 35 33 34 32 36 40 38 39 37 3 41 45 43 44 42 5 9 7 8 6 20 24 22 23 21 15 19 17 18 16 10 14 12 13 11 10 11 12 13 14 46 47 48 49 50 31 32 33 34 35 36 37 38 39 40 5 6 7 8 9 41 45 42 44 3 43 20 21 22 23 24 15 16 17 18 19 25 1 4 2 0 26 27 28 29 30 11 14 13 10 12 47 50 49 46 48 32 35 34 31 33 37 40 39 36 38 6 9 8 5 7 43 44 41 3 42 45 21 24 23 20 22 16 19 18 15 17 1 0 2 25 4 27 30 29 26 28 12 13 11 14 10 48 49 47 50 46 33 34 32 35 31 38 39 37 40 36 7 8 6 9 5 45 43 44 42 41 3 22 23 21 24 20 17 18 16 19 15 4 2 1 0 25 28 29 27 30 26 14 12 10 11 13 50 48 46 47 49 35 33 31 32 34 40 38 36 37 39 9 7 5 6 8 44 42 3 45 43 41 24 22 20 21 23 19 17 15 16 18 0 4 25 1 2 30 28 26 27 29 13 10 14 12 11 49 46 50 48 47 34 31 35 33 32 39 36 40 38 37 8 5 9 7 6 42 3 43 41 45 44 23 20 24 22 21 18 15 19 17 16 2 25 0 4 1 29 26 30 28 27 46 47 48 49 50 25 1 4 2 0 36 37 38 39 40 41 42 43 44 45 31 32 33 34 35 5 20 21 22 23 24 9 6 8 3 7 10 11 12 13 14 26 27 28 29 30 15 16 17 18 19 47 50 49 46 48 1 0 2 25 4 37 40 39 36 38 42 45 44 41 43 32 35 34 31 33 7 21 24 23 20 22 8 5 3 6 9 11 14 13 10 12 27 30 29 26 28 16 19 18 15 17 48 49 47 50 46 4 2 1 0 25 38 39 37 40 36 43 44 42 45 41 33 34 32 35 31 9 22 23 21 24 20 7 8 6 5 3 12 13 11 14 10 28 29 27 30 26 17 18 16 19 15 50 48 46 47 49 0 4 25 1 2 40 38 36 37 39 45 43 41 42 44 35 33 31 32 34 8 24 22 20 21 23 6 3 9 7 5 14 12 10 11 13 30 28 26 27 29 19 17 15 16 18 49 46 50 48 47 2 25 0 4 1 39 36 40 38 37 44 41 45 43 42 34 31 35 33 32 6 23 20 24 22 21 3 7 5 9 8 13 10 14 12 11 29 26 30 28 27 18 15 19 17 16 31 32 33 34 35 36 37 38 39 40 15 16 17 18 19 10 11 12 13 14 26 27 28 29 30 20 5 6 7 8 9 41 42 43 44 45 24 21 23 3 22 46 47 48 49 50 25 1 4 2 0 32 35 34 31 33 37 40 39 36 38 16 19 18 15 17 11 14 13 10 12 27 30 29 26 28 22 6 9 8 5 7 42 45 44 41 43 23 20 3 21 24 47 50 49 46 48 1 0 2 25 4 33 34 32 35 31 38 39 37 40 36 17 18 16 19 15 12 13 11 14 10 28 29 27 30 26 24 7 8 6 9 5 43 44 42 45 41 22 23 21 20 3 48 49 47 50 46 4 2 1 0 25 35 33 31 32 34 40 38 36 37 39 19 17 15 16 18 14 12 10 11 13 30 28 26 27 29 23 9 7 5 6 8 45 43 41 42 44 21 3 24 22 20 50 48 46 47 49 0 4 25 1 2 34 31 35 33 32 39 36 40 38 37 18 15 19 17 16 13 10 14 12 11 29 26 30 28 27 21 8 5 9 7 6 44 41 45 43 42 3 22 20 24 23 49 46 50 48 47 2 25 0 4 1 36 37 38 39 40 20 21 22 23 24 5 6 7 8 9 26 27 28 29 30 46 47 48 49 50 15 10 11 12 13 14 25 1 4 2 0 41 42 43 44 45 19 16 18 3 17 31 32 33 34 35 37 40 39 36 38 21 24 23 20 22 6 9 8 5 7 27 30 29 26 28 47 50 49 46 48 17 11 14 13 10 12 1 0 2 25 4 42 45 44 41 43 18 15 3 16 19 32 35 34 31 33 38 39 37 40 36 22 23 21 24 20 7 8 6 9 5 28 29 27 30 26 48 49 47 50 46 19 12 13 11 14 10 4 2 1 0 25 43 44 42 45 41 17 18 16 15 3 33 34 32 35 31 40 38 36 37 39 24 22 20 21 23 9 7 5 6 8 30 28 26 27 29 50 48 46 47 49 18 14 12 10 11 13 0 4 25 1 2 45 43 41 42 44 16 3 19 17 15 35 33 31 32 34 39 36 40 38 37 23 20 24 22 21 8 5 9 7 6 29 26 30 28 27 49 46 50 48 47 16 13 10 14 12 11 2 25 0 4 1 44 41 45 43 42 3 17 15 19 18 34 31 35 33 32 26 27 28 29 30 31 32 33 34 35 41 42 43 44 45 20 21 22 23 24 25 1 4 2 0 10 15 16 17 18 19 46 47 48 49 50 5 6 7 8 9 36 37 38 39 40 14 11 13 3 12 27 30 29 26 28 32 35 34 31 33 42 45 44 41 43 21 24 23 20 22 1 0 2 25 4 12 16 19 18 15 17 47 50 49 46 48 6 9 8 5 7 37 40 39 36 38 13 10 3 11 14 28 29 27 30 26 33 34 32 35 31 43 44 42 45 41 22 23 21 24 20 4 2 1 0 25 14 17 18 16 19 15 48 49 47 50 46 7 8 6 9 5 38 39 37 40 36 12 13 11 10 3 30 28 26 27 29 35 33 31 32 34 45 43 41 42 44 24 22 20 21 23 0 4 25 1 2 13 19 17 15 16 18 50 48 46 47 49 9 7 5 6 8 40 38 36 37 39 11 3 14 12 10 29 26 30 28 27 34 31 35 33 32 44 41 45 43 42 23 20 24 22 21 2 25 0 4 1 11 18 15 19 17 16 49 46 50 48 47 8 5 9 7 6 39 36 40 38 37 3 12 10 14 13 Вспомогательные квадраты. выданные программой V = 1 3 4 6 7 5 8 9 10 2 3 2 5 7 4 8 6 10 1 9 2 1 3 8 6 9 10 4 5 7 5 6 1 4 9 10 3 2 7 8 4 8 2 10 5 7 9 1 3 6 7 9 10 1 8 6 2 5 4 3 6 4 9 5 10 2 7 3 8 1 10 7 6 9 1 3 4 8 2 5 8 10 7 2 3 1 5 6 9 4 9 5 8 3 2 4 1 7 6 10 Q = 1 3 2 5 6 4 3 2 4 6 1 5 5 6 3 1 4 2 2 5 6 4 3 1 6 4 1 2 5 3 4 1 5 3 2 6 P1 = 3 4 5 6 2 4 2 6 3 5 5 6 4 2 3 2 5 3 4 6 6 3 2 5 4 Сразу видно, что квадрат Q плохой, в том смысле, что не имеет ортогонального соквадрата. Следовательно, данный расклад не годится для построения ортогональной пары ДЛК 51-го порядка методом Линдера, если правильно понимаю. Ну, имеем хотя бы одиночный ДЛК, к которому можно поискать ортогональные ДЛК другими методами. Утилита Harry White подтверждает, что построенный квадрат диагональный. Замечу, что для построения ортогональной пары ЛК 51-го порядка нет преград, так как 51=3*17 и, следовательно, работает метод составных квадратов. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ох, тяжёлая это работа... :) Долго думала, как мне быстро проверить группу ОДЛК 12-го порядка на наличие в этой группе хотя бы одной ортогональной пары. У меня нет программы проверки ортогональности для такого случая, её надо соорудить. Ну вот пришла мысль воспользоваться утилитой Hary White. Но... тут я теряюсь в логике данной утилиты. Сначала ввожу для проверки 2199 ОДЛК (без исходного ДЛК, построенного методом Гергели). Внимание! Утилита выдаёт следующий результат Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
2199 diagonal Latin
2199 axial symmetric
2199 nfrТо есть обнаружены все 2199 ДЛК, все они симметричные по Гергели/Брауну и все нормализованные. Это всё так и есть. И - в этой группе не обнаружено ни одной ортогональной пары!! Проверка выполнена??? Ни у одного ДЛК этой группы нет ортогонального ДЛК в этой же группе. А теперь ввожу для проверки все эти 2199 ДЛК и исходный ДЛК, построенный методом Гергели. Внимание! Утилита выдаёт следующий результат Order? 12
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_2.txt
Counts
------
2200 diagonal Latin
2200 axial symmetric
2199 nfr
1 orthogonal pairТеперь обнаружено 2200 ДЛК, все они симметричные по Гергели/Брауну, 2199 ДЛК нормализованные (исходный ДЛК я не нормализовала). Это всё понятно, так оно и есть. Но почему "1 orthogonal pair"??? Абсолютно не понимаю, какая тут логика. Самый первый ДЛК введённой группы - исходный ДЛК, и все следующие 2199 ДЛК ему ортогональны. Я проверила ортогональность всех 2199 ДЛК исходному. Тогда почему утилита Harry сообщает только об одной ортогональной паре? Ничего не понимаю :( Ну, а в первом случае буду считать, что проверка группы из 2199 ДЛК на ортогональность между этими ДЛК выполнена, ни одной ортогональной пары не найдено в данной группе. Проверила несколько первых ДЛК из 2199 на марьяжные ДЛК программой Белышева. Они имеют ортогональные диагональные соквадраты! Но очень мало, 17, 22... И тут возникает такой вопрос: не может ли группа MODLS появиться на этом втором уровне??? А почему бы и нет? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
|
Send message Joined: 14 Jan 19 Posts: 119 Credit: 574 RAC: 0 |
Hello Natalia! I am trying my luck at programming for DLK n>10. And I made a multi-threaded program similar to ortogon_u (i do not have a source). I do not know if correct yet. DLK 12 from message square: 0 1 2 3 4 5 6 7 8 9 10 11 4 2 6 0 3 10 1 8 11 5 9 7 8 0 4 10 5 2 9 6 1 7 11 3 10 3 0 5 9 4 7 2 6 11 8 1 5 4 3 2 10 11 0 1 9 8 7 6 2 5 10 7 0 3 8 11 4 1 6 9 6 7 8 9 1 0 11 10 2 3 4 5 1 8 11 6 2 7 4 9 5 0 3 10 9 6 1 4 11 8 3 0 7 10 5 2 7 9 5 11 8 1 10 3 0 6 2 4 11 10 9 8 7 6 5 4 3 2 1 0 3 11 7 1 6 9 2 5 10 4 0 8 isLK: 1 isDLK: 1 width: 12 init_trans(12) used 495 nodes num_trans: 5718 init_disjoint(12) used 145 heads and 68761 nodes dance_mt: using 16 threads for 292 rows in column 42 l(1) 292 / 292 isODLK: 2199 orthogonal mates 57 seconds Appears to be OK! DLK 11 No3 from message width: 11 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 0 1 2 6 7 8 9 10 0 1 2 3 4 5 9 10 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 0 4 5 6 7 8 9 10 0 1 2 3 7 8 9 10 0 1 2 3 4 5 6 10 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 0 1 5 6 7 8 9 10 0 1 2 3 4 8 9 10 0 1 2 3 4 5 6 7 isLK: 1 isDLK: 1 init_trans(11) used 420 nodes num_trans: 4700 init_disjoint(11) used 122 heads and 51822 nodes dance_mt: using 16 threads for 396 rows in column 7 l(1) 396 / 396 isODLK: 0 orthogonal mates time: 3m 2s Is this correct Where error? Checking more squares... |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Tomas я очень рада, что вы заинтересовались этой темой. Замечательно, что вы сделали программу аналогичную программе Белышева ortogon_u. Программа Белышева работает с ДЛК 12-го порядка в таком виде 0 1 2 3 4 5 6 7 8 9 A B 4 2 6 0 3 A 1 8 B 5 9 7 8 0 4 A 5 2 9 6 1 7 B 3 A 3 0 5 9 4 7 2 6 B 8 1 5 4 3 2 A B 0 1 9 8 7 6 2 5 A 7 0 3 8 B 4 1 6 9 6 7 8 9 1 0 B A 2 3 4 5 1 8 B 6 2 7 4 9 5 0 3 A 9 6 1 4 B 8 3 0 7 A 5 2 7 9 5 B 8 1 A 3 0 6 2 4 B A 9 8 7 6 5 4 3 2 1 0 3 B 7 1 6 9 2 5 A 4 0 8 Вот протокол работы программы Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 5718 Соквадратов: 2199 Время в сек: 1155 1 28 13 4 2 2 Для выхода нажмите любую клавишу: Всё верно, этот ДЛК имеет 2199 ортогональных диагональных соквадратов. Следующий ДЛК преобразован к виду 0 1 2 3 4 5 6 7 8 9 A 3 4 5 6 7 8 9 A 0 1 2 6 7 8 9 A 0 1 2 3 4 5 9 A 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 A 0 4 5 6 7 8 9 A 0 1 2 3 7 8 9 A 0 1 2 3 4 5 6 A 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 A 0 1 5 6 7 8 9 A 0 1 2 3 4 8 9 A 0 1 2 3 4 5 6 7 Протокол работы программы Белышева ortogonal_u Проверка ДЛК11 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 4665 Соквадратов: 26914 Время в сек: 3535 1 83 24 8 4 1 Для выхода нажмите любую клавишу: Этот ДЛК имеет 26914 ортогональных диагональных соквадратов. У вас этот ДЛК имеет 0 ортогональных диагональных соквадратов? Почему это не совпадает с результатом программы Белышева? К сожалению, у меня нет источника программы Белышева. PS. num_trans: 4700 Это у вас количество трансверсалей в ДЛК? Обратите внимание, что в программе Белышева находятся только диагональные трансверсали Д-трансверсалей: 4665 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Я посмотрела в своём архиве все предыдущие версии программы Белышева ortogonal_u. И нашла источники для версии ortogonal_u(2). Я могу прислать вам это. PS. Уже отправила. Пожалуйста, дайте мне знать, получили ли архив (отправила только в один адрес). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, идём дальше. Порядок 52 не проблемный, так как 52=13*4. Порядок 53 тоже не проблемный, так как 53 простое число к нашему удовольствию :) Порядок 54 не проблемный для ортогональных пар ЛК, так как 54=3*18. Для ортогональной пары ДЛК данного порядка работает метод Пелегрино-Ланселотти, реализованный программно Черновым. У меня где-то была построена эта ортогональная пара ДЛК. Сейчас найду и выложу. Порядки 55 и 56 не проблемные. Порядок 57 не проблемный для ортогональных пар ЛК, так как 57=3*19. А вот для ортогональных пар ДЛК этот порядок проблемный. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger