Идём дальше.
Порядок 35 не проблемный, так как 35=5*7.
Порядок 36 не проблемный, так как 36=4*9.
Я обещала показать построение ортогональной пары 36-го порядка методом Пелегрино-Ланселотти, описанным в статье Чернова
http://alex-black.ru/article.php?content=124
и на основе построенной в этой статье ортогональной пары ДЛК 12-го порядка, вот этой



Я в то время строила ортогональную пару ДЛК 36-го порядка данным методом, но не помню, какую брала исходную ортогональную пару ДЛК 12-го порядка.
Сейчас построю на основе показанной ортогональной пары.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Готово!
Строится мгновенно.

16 5 6 7 4 3 0 10 9 8 11 1 2 15 12 13 14 17 18 20 23 22 21 34 25 26 35 24 33 32 27 30 31 28 29 19 
7 18 5 4 1 6 8 2 10 11 3 9 13 0 15 14 19 12 22 16 20 21 32 23 24 27 26 33 34 35 28 25 30 29 17 31 
5 4 19 6 3 9 7 0 8 2 10 11 15 14 1 12 17 23 13 18 22 25 20 21 26 33 34 35 32 31 24 27 28 16 30 29 
6 7 4 17 11 1 2 5 0 10 9 8 12 13 14 3 21 19 16 15 27 20 23 22 35 24 33 32 29 34 25 26 18 30 31 28 
1 11 3 2 20 0 5 9 7 6 8 4 19 21 17 16 10 18 15 31 13 12 22 14 34 29 32 25 30 27 26 23 24 35 28 33 
9 3 0 1 2 22 11 7 4 5 6 10 23 17 18 19 16 8 29 13 14 15 12 20 31 32 27 34 25 28 21 24 33 26 35 30 
0 1 2 8 6 10 23 3 11 7 4 5 18 19 16 22 12 30 9 17 21 13 14 15 27 34 25 28 35 20 31 32 29 24 33 26 
3 2 10 0 8 4 1 21 5 9 7 6 17 16 20 18 28 14 19 11 15 23 13 12 32 25 30 27 22 33 34 29 26 31 24 35 
11 10 9 5 0 7 4 8 12 1 2 3 21 20 23 26 18 13 14 22 6 19 16 17 29 30 31 15 27 24 33 28 35 34 25 32 
8 9 7 11 5 2 10 6 3 14 1 0 22 23 24 21 15 16 20 12 17 4 19 18 28 31 13 29 26 25 30 35 32 33 34 27 
10 6 8 9 7 11 3 4 1 0 15 2 20 35 22 23 13 21 17 14 19 18 5 16 30 12 28 31 24 29 32 33 34 27 26 25 
4 8 11 10 9 5 6 1 2 3 0 13 33 22 21 20 23 15 12 19 16 17 18 7 14 28 29 30 31 26 35 34 25 32 27 24 
12 27 13 16 15 19 14 23 22 21 20 17 28 18 7 25 26 29 30 32 35 34 33 31 8 0 24 2 5 11 10 3 6 1 4 9 
25 14 18 15 17 13 21 12 23 20 19 22 16 30 27 5 31 24 34 28 32 33 29 35 2 10 0 26 9 7 1 8 3 4 11 6 
18 15 17 13 19 35 16 14 21 12 23 20 27 26 31 24 29 22 25 30 34 28 3 33 0 5 9 7 11 6 2 10 1 8 32 4 
13 16 15 19 33 17 12 18 14 23 22 21 24 25 26 29 20 31 28 27 30 32 35 1 7 2 5 11 4 9 8 0 10 3 6 34 
17 20 29 12 23 14 18 22 16 13 21 15 31 33 19 28 32 10 27 35 25 24 34 26 9 4 11 8 3 30 0 6 2 7 1 5 
22 19 14 31 12 21 20 16 15 18 13 23 35 29 30 17 8 34 33 25 26 27 24 32 6 11 10 9 28 1 4 2 5 0 7 3 
14 17 12 21 13 23 22 19 20 16 26 18 30 31 28 34 24 32 35 29 33 2 15 27 10 9 8 1 7 3 6 11 4 25 5 0 
19 12 23 14 21 15 17 20 18 22 16 24 29 28 32 30 34 26 31 33 0 35 25 13 11 8 3 10 1 5 9 4 27 6 2 7 
20 23 22 18 14 16 15 34 13 17 12 19 4 32 35 27 30 25 26 21 24 31 28 29 33 3 6 0 10 2 5 1 7 9 8 11 
21 22 16 20 18 12 32 13 19 15 17 14 34 6 25 33 27 28 23 24 29 26 31 30 1 35 2 4 0 8 3 7 11 5 9 10 
23 13 21 22 16 20 19 15 17 30 18 12 32 24 34 35 25 33 11 26 31 14 27 28 3 7 1 6 2 4 29 5 9 10 0 8 
15 21 20 23 22 18 13 17 28 19 14 16 26 34 33 32 35 27 24 9 12 29 30 25 5 1 4 3 6 0 7 31 8 11 10 2 
30 31 27 29 25 26 28 35 34 33 32 7 14 3 0 1 2 5 6 8 11 10 9 24 4 17 18 19 16 15 12 22 21 20 23 13 
29 28 31 25 24 27 33 30 35 32 5 34 1 12 3 2 7 0 10 4 8 9 26 11 19 6 17 16 13 18 20 14 22 23 15 21 
31 25 24 27 26 34 29 28 33 4 35 32 3 2 13 0 5 11 1 6 10 30 8 9 17 16 7 18 15 21 19 12 20 14 22 23 
27 29 25 26 32 24 30 31 6 35 34 33 0 1 2 15 9 7 4 3 28 8 11 10 18 19 16 5 23 13 14 17 12 22 21 20 
24 32 26 30 35 28 31 11 29 27 33 25 7 9 5 4 22 6 3 34 1 0 10 2 13 23 15 14 8 12 17 21 19 18 20 16 
34 26 28 24 30 33 9 29 25 31 27 35 11 5 6 7 4 20 32 1 2 3 0 8 21 15 12 13 14 10 23 19 16 17 18 22 
28 24 30 33 27 8 34 26 32 29 25 31 6 7 4 10 0 35 21 5 9 1 2 3 12 13 14 20 18 22 11 15 23 19 16 17 
26 30 35 28 10 25 24 32 31 34 29 27 5 4 8 6 33 2 7 23 3 11 1 0 15 14 22 12 20 16 13 9 17 21 19 18 
32 35 34 3 28 29 25 33 27 24 30 26 9 8 11 31 6 1 2 10 18 7 4 5 23 22 21 17 12 19 16 20 0 13 14 15 
33 34 1 32 31 30 35 27 26 25 24 28 10 11 29 9 3 4 8 0 5 16 7 6 20 21 19 23 17 14 22 18 15 2 13 12 
35 0 33 34 29 32 26 25 24 28 31 30 8 27 10 11 1 9 5 2 7 6 17 4 22 18 20 21 19 23 15 16 13 12 3 14 
2 33 32 35 34 31 27 24 30 26 28 29 25 10 9 8 11 3 0 7 4 5 6 19 16 20 23 22 21 17 18 13 14 15 12 1 

32 7 4 9 10 5 6 8 11 2 1 3 0 27 24 25 26 33 34 30 29 28 31 18 17 14 13 12 15 16 19 23 20 21 22 35 
4 35 10 7 6 9 11 5 1 8 0 2 24 3 26 27 34 25 29 33 31 30 17 28 13 18 15 14 19 12 20 16 22 23 32 21 
9 4 33 10 3 1 7 0 8 6 2 11 25 24 5 26 35 31 27 32 30 19 28 29 12 13 16 15 18 22 14 17 23 34 21 20 
7 10 9 34 2 0 3 4 5 11 8 1 27 26 25 6 28 32 35 24 16 29 30 31 14 15 12 19 21 17 18 13 33 20 23 22 
1 9 11 2 24 8 0 7 6 3 10 5 31 25 29 28 4 30 32 14 34 35 26 33 22 12 20 21 13 23 17 27 19 18 15 16 
10 2 1 8 11 27 4 3 0 5 6 9 26 28 31 30 29 7 13 35 32 33 34 25 15 21 22 23 20 14 24 18 17 16 19 12 
2 11 8 4 5 10 25 1 7 0 3 6 28 29 30 24 33 15 9 31 27 32 35 34 21 20 23 13 16 26 12 22 14 17 18 19 
8 1 7 11 9 6 2 26 3 4 5 0 30 31 27 29 12 34 28 10 35 24 33 32 23 22 14 20 25 19 21 15 18 13 16 17 
5 0 3 1 7 11 8 6 28 10 9 4 33 32 35 22 27 29 30 34 2 26 25 24 16 17 18 31 14 20 23 19 21 15 12 13 
3 6 2 0 8 4 5 11 9 31 7 10 35 34 21 32 30 24 33 29 25 1 27 26 18 19 28 17 23 13 16 20 12 22 14 15 
6 8 0 5 1 3 10 2 4 9 29 7 34 23 32 33 31 35 26 28 24 25 11 27 19 30 17 16 22 18 15 21 13 12 20 14 
11 5 6 3 0 2 1 9 10 7 4 30 20 33 34 35 32 28 31 25 26 27 24 8 29 16 19 18 17 21 22 12 15 14 13 23 
23 3 17 22 21 12 15 19 16 13 14 20 8 18 28 1 2 9 10 6 5 4 7 11 34 31 0 27 24 29 30 26 25 32 35 33 
0 20 21 18 15 22 16 12 14 19 23 13 17 11 2 31 10 1 5 9 7 6 8 4 28 33 24 3 30 27 25 29 35 26 34 32 
22 17 12 21 20 7 18 23 19 15 13 16 1 0 9 2 11 14 3 8 6 10 32 5 27 28 29 24 33 35 31 34 26 30 4 25 
18 21 22 15 4 23 20 17 12 16 19 14 3 2 1 10 13 8 11 0 9 5 6 35 31 24 27 30 32 34 33 28 29 25 26 7 
14 22 5 13 17 19 23 18 15 20 21 12 7 1 16 4 0 26 8 3 10 11 2 9 35 27 25 32 28 6 34 31 30 33 24 29 
21 13 14 6 16 18 17 20 23 12 15 22 2 4 7 19 25 3 0 11 8 9 10 1 24 32 35 26 5 31 28 33 34 29 30 27 
13 16 19 17 12 21 22 14 18 23 11 15 4 5 6 0 9 2 1 7 3 34 20 10 32 25 26 28 29 24 27 35 31 8 33 30 
19 14 18 16 22 15 13 21 20 17 12 8 6 7 3 5 1 10 4 2 33 0 9 23 26 35 31 25 27 30 32 24 11 28 29 34 
12 23 20 14 18 16 19 10 13 21 22 17 29 8 11 7 3 5 6 15 4 2 1 0 9 34 33 35 31 25 26 30 32 24 27 28 
20 15 13 23 19 17 9 16 22 14 18 21 11 30 4 8 6 0 12 5 1 7 3 2 33 10 32 34 26 28 29 25 27 35 31 24 
15 19 23 12 14 20 21 13 17 1 16 18 10 6 8 9 7 11 24 4 0 22 5 3 30 26 34 29 35 33 2 32 28 27 25 31 
16 12 15 20 23 13 14 22 2 18 17 19 5 9 10 11 8 4 7 27 21 3 0 6 25 29 30 33 34 32 35 1 24 31 28 26 
29 26 25 24 27 28 31 35 32 33 34 23 9 15 12 13 14 21 22 18 17 16 19 30 20 6 5 2 1 0 3 7 4 11 8 10 
25 30 27 26 31 24 32 28 34 35 20 33 12 10 14 15 22 13 17 21 19 18 29 16 5 23 1 6 3 2 4 0 8 7 9 11 
24 25 28 27 30 34 26 29 35 22 33 32 13 12 0 14 23 19 15 20 18 31 16 17 2 5 21 1 10 8 6 9 7 3 11 4 
26 27 24 31 33 29 30 25 21 32 35 34 15 14 13 3 16 20 23 12 28 17 18 19 6 1 2 22 11 9 10 5 0 4 7 8 
34 24 32 33 25 35 29 15 31 30 27 28 19 13 17 16 5 18 20 26 22 23 14 21 8 2 4 11 12 7 9 6 3 10 1 0 
27 33 34 35 32 26 12 30 29 28 31 24 14 16 19 18 17 6 25 23 20 21 22 13 1 11 8 7 4 15 5 10 9 0 3 2 
33 32 35 25 28 14 24 34 26 29 30 31 16 17 18 12 21 27 2 19 15 20 23 22 11 4 7 5 0 1 13 8 6 9 10 3 
35 34 26 32 13 31 33 27 30 25 28 29 18 19 15 17 24 22 16 1 23 12 21 20 7 8 6 4 2 3 11 14 10 5 0 9 
28 29 30 19 26 32 35 31 33 27 24 25 21 20 23 34 15 17 18 22 11 14 13 12 0 9 10 8 6 4 7 3 16 1 2 5 
30 31 16 29 35 25 28 32 24 34 26 27 23 22 33 20 18 12 21 17 13 8 15 14 10 3 11 9 7 5 0 4 2 19 6 1 
31 18 29 28 34 30 27 33 25 24 32 26 22 35 20 21 19 23 14 16 12 13 4 15 3 7 9 0 8 10 1 11 5 2 17 6 
17 28 31 30 29 33 34 24 27 26 25 35 32 21 22 23 20 16 19 13 14 15 12 7 4 0 3 10 9 11 8 2 1 6 5 18

Утилита Harry White подтверждает ортогональность этих ДЛК

Order? 36

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_3.txt

Counts
------
         2 diagonal Latin
         1 orthogonal pair

Классная ортогональная пара!

Ещё этим методом предстоит построить ортогональную пару ДЛК 42-го порядка, которую в то время мне построить не удалось.
Нужна хорошая ортогональная пара ДЛК 14-го порядка, чтобы в ДЛК этой пары нашлись нужные трансверсали.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Тэк-с, порядок 37 - простое число, на наше счастье :)
Порядок 38 проблемный.
Ну, построить одиночный ДЛК данного порядка можно методом Гергели.
А вот с ортогональной парой ДЛК сложнее.
В моих статьях вроде не встречалась такая ортогональная пара ДЛК.
Надежда на метод Линдера.
Пробовала, но программа плохо шевелится, работает вроде, но долго ли будет искать - чёрту даже неизвестно.
Метод Ли Жу для этого порядка тоже должен работать, но та же история: программа уходит в глубокую задумчивость.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Пример (метод Линдера)

Microsoft Windows [Version 6.1.7601]
(c) Корпорация Майкрософт (Microsoft Corp.), 2009. Все права защищены.
C:\Users\Дом>cd C:\Users\Дом\Downloads\test_dols_2
C:\Users\Дом\Downloads\test_dols_2>test 10 8 11 >d38.txt

Программа работает, об ошибках не сообщает.
Видимо, с увеличением порядка ДЛК программа будет работать всё медленнее.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

В статье http://www.natalimak1.narod.ru/dlk.htm приведена программа для построения методом Гергели ДЛК порядков n = 2k, где k – нечётное число не кратное 3.
Проверила сейчас для порядка n=38 (k=19), программа работает!
Вот построенный ДЛК 38-го порядка

1 21 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 2 20 
2 3 23 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 20 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 4 22 21 
3 4 5 25 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 21 20 0 37 36 35 34 33 32 31 30 29 28 27 26 6 24 23 22 
4 5 6 7 27 9 10 11 12 13 14 15 16 17 18 19 1 2 3 22 21 20 0 37 36 35 34 33 32 31 30 29 28 8 26 25 24 23 
5 6 7 8 9 29 11 12 13 14 15 16 17 18 19 1 2 3 4 23 22 21 20 0 37 36 35 34 33 32 31 30 10 28 27 26 25 24 
6 7 8 9 10 11 31 13 14 15 16 17 18 19 1 2 3 4 5 24 23 22 21 20 0 37 36 35 34 33 32 12 30 29 28 27 26 25 
7 8 9 10 11 12 13 33 15 16 17 18 19 1 2 3 4 5 6 25 24 23 22 21 20 0 37 36 35 34 14 32 31 30 29 28 27 26 
8 9 10 11 12 13 14 15 35 17 18 19 1 2 3 4 5 6 7 26 25 24 23 22 21 20 0 37 36 16 34 33 32 31 30 29 28 27 
9 10 11 12 13 14 15 16 17 37 19 1 2 3 4 5 6 7 8 27 26 25 24 23 22 21 20 0 18 36 35 34 33 32 31 30 29 28 
10 11 12 13 14 15 16 17 18 19 20 2 3 4 5 6 7 8 9 28 27 26 25 24 23 22 21 1 0 37 36 35 34 33 32 31 30 29 
11 12 13 14 15 16 17 18 19 1 2 22 4 5 6 7 8 9 10 29 28 27 26 25 24 23 3 21 20 0 37 36 35 34 33 32 31 30 
12 13 14 15 16 17 18 19 1 2 3 4 24 6 7 8 9 10 11 30 29 28 27 26 25 5 23 22 21 20 0 37 36 35 34 33 32 31 
13 14 15 16 17 18 19 1 2 3 4 5 6 26 8 9 10 11 12 31 30 29 28 27 7 25 24 23 22 21 20 0 37 36 35 34 33 32 
14 15 16 17 18 19 1 2 3 4 5 6 7 8 28 10 11 12 13 32 31 30 29 9 27 26 25 24 23 22 21 20 0 37 36 35 34 33 
15 16 17 18 19 1 2 3 4 5 6 7 8 9 10 30 12 13 14 33 32 31 11 29 28 27 26 25 24 23 22 21 20 0 37 36 35 34 
16 17 18 19 1 2 3 4 5 6 7 8 9 10 11 12 32 14 15 34 33 13 31 30 29 28 27 26 25 24 23 22 21 20 0 37 36 35 
17 18 19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 34 16 35 15 33 32 31 30 29 28 27 26 25 24 23 22 21 20 0 37 36 
18 19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 36 17 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 0 37 
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19 
37 0 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 17 36 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 19 18 
36 37 0 20 21 22 23 24 25 26 27 28 29 30 31 32 33 15 35 16 34 14 13 12 11 10 9 8 7 6 5 4 3 2 1 19 18 17 
35 36 37 0 20 21 22 23 24 25 26 27 28 29 30 31 13 33 34 15 14 32 12 11 10 9 8 7 6 5 4 3 2 1 19 18 17 16 
34 35 36 37 0 20 21 22 23 24 25 26 27 28 29 11 31 32 33 14 13 12 30 10 9 8 7 6 5 4 3 2 1 19 18 17 16 15 
33 34 35 36 37 0 20 21 22 23 24 25 26 27 9 29 30 31 32 13 12 11 10 28 8 7 6 5 4 3 2 1 19 18 17 16 15 14 
32 33 34 35 36 37 0 20 21 22 23 24 25 7 27 28 29 30 31 12 11 10 9 8 26 6 5 4 3 2 1 19 18 17 16 15 14 13 
31 32 33 34 35 36 37 0 20 21 22 23 5 25 26 27 28 29 30 11 10 9 8 7 6 24 4 3 2 1 19 18 17 16 15 14 13 12 
30 31 32 33 34 35 36 37 0 20 21 3 23 24 25 26 27 28 29 10 9 8 7 6 5 4 22 2 1 19 18 17 16 15 14 13 12 11 
29 30 31 32 33 34 35 36 37 0 1 21 22 23 24 25 26 27 28 9 8 7 6 5 4 3 2 20 19 18 17 16 15 14 13 12 11 10 
28 29 30 31 32 33 34 35 36 18 0 20 21 22 23 24 25 26 27 8 7 6 5 4 3 2 1 19 37 17 16 15 14 13 12 11 10 9 
27 28 29 30 31 32 33 34 16 36 37 0 20 21 22 23 24 25 26 7 6 5 4 3 2 1 19 18 17 35 15 14 13 12 11 10 9 8 
26 27 28 29 30 31 32 14 34 35 36 37 0 20 21 22 23 24 25 6 5 4 3 2 1 19 18 17 16 15 33 13 12 11 10 9 8 7 
25 26 27 28 29 30 12 32 33 34 35 36 37 0 20 21 22 23 24 5 4 3 2 1 19 18 17 16 15 14 13 31 11 10 9 8 7 6 
24 25 26 27 28 10 30 31 32 33 34 35 36 37 0 20 21 22 23 4 3 2 1 19 18 17 16 15 14 13 12 11 29 9 8 7 6 5 
23 24 25 26 8 28 29 30 31 32 33 34 35 36 37 0 20 21 22 3 2 1 19 18 17 16 15 14 13 12 11 10 9 27 7 6 5 4 
22 23 24 6 26 27 28 29 30 31 32 33 34 35 36 37 0 20 21 2 1 19 18 17 16 15 14 13 12 11 10 9 8 7 25 5 4 3 
21 22 4 24 25 26 27 28 29 30 31 32 33 34 35 36 37 0 20 1 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 23 3 2 
20 2 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 0 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 21 1 
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Симпатичный квадратик.
Утилита Harry White отметила в этом ДЛК симметричность по Гергели/Брауну.
Ну и как вы думаете: у этого симпатичного симметричного ДЛК есть ортогональные ДЛК?
Будем надеяться, что есть.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ох, 39 тоже проблемный порядок.
Ничего пока нет у меня для этого порядка, даже одиночного ДЛК.
У кого есть, покажите, пожалуйста.
Разумеется, для ортогональных пар ЛК этот порядок не проблемный, так как 39=3*13.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ничего не получилось с построением ортогональной пары ДЛК 39-го порядка.
Оставляю пока этот порядок.

Порядки 40 и 41 не проблемные.
Порядок 42 проблемный для ортогональных пар ДЛК, а для ортогональных пар ЛК - нет, так как 42=3*14.

Отлично сработал метод Пелегрино-Ланселотти по программе Чернова.
Только было трудно найти хорошую ортогональную пару ДЛК 14-го порядка.
Нашла её среди ортогональных пар для ДЛК Гергели.
Вот эта ортогональная пара

1 9 3 4 5 6 7 0 13 12 11 10 2 8
2 3 11 5 6 7 1 8 0 13 12 4 10 9
3 4 5 13 7 1 2 9 8 0 6 12 11 10
4 5 6 7 8 2 3 10 9 1 0 13 12 11
5 6 7 1 2 10 4 11 3 9 8 0 13 12
6 7 1 2 3 4 12 5 11 10 9 8 0 13
0 1 2 3 4 5 6 13 12 11 10 9 8 7
13 0 8 9 10 11 5 12 4 3 2 1 7 6
12 13 0 8 9 3 11 4 10 2 1 7 6 5
11 12 13 0 1 9 10 3 2 8 7 6 5 4
10 11 12 6 0 8 9 2 1 7 13 5 4 3
9 10 4 12 13 0 8 1 7 6 5 11 3 2
8 2 10 11 12 13 0 7 6 5 4 3 9 1
7 8 9 10 11 12 13 6 5 4 3 2 1 0

 0  1  2  3  4  5  6  7  8  9  10  11  12  13 
 3  6  0  5  10  4  13  9  2  7  12  1  8  11 
 8  0  10  11  12  9  5  2  4  13  3  6  7  1 
 9  7  8  1  6  10  11  13  12  2  0  5  4  3 
 6  9  13  7  2  0  8  11  10  4  1  12  3  5 
 11  8  3  4  13  7  0  12  9  10  5  2  1  6 
 5  4  1  9  11  13  12  10  7  8  6  3  0  2 
 2  10  5  0  9  6  1  3  13  12  7  8  11  4 
 1  12  9  8  7  3  2  4  5  6  11  10  13  0 
 12  13  4  6  5  8  3  1  0  11  9  7  2  10 
 4  5  11  2  3  12  10  8  1  0  13  9  6  7 
 13  2  12  10  0  11  7  6  3  1  8  4  5  9 
 10  11  7  13  8  1  4  5  6  3  2  0  9  12 
 7  3  6  12  1  2  9  0  11  5  4  13  10  8 

Первый ДЛК - построенный методом Гергели, второй ДЛК - ортогональный ему.
Для этой пары ортогональная пара ДЛК 42-го порядка построилась мгновенно.
Далее покажу её.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Ортогональная пара ДЛК 42-го порядка, построенная методом Пелегрино-Ланселотти по программе Чернова
(с использованием найденной мной ортогональной пары ДЛК 14-го порядка)

15 10 2 3 4 5 6 8 0 13 12 11 1 9 7 23 17 18 19 20 21 14 27 26 25 24 16 30 36 35 41 29 32 33 39 31 37 38 40 34 28 22 
1 17 12 4 5 6 7 9 8 0 13 3 11 10 16 2 25 19 20 21 15 22 14 27 26 18 34 23 28 41 40 32 33 39 36 30 31 37 38 29 24 35 
2 3 19 0 6 7 1 10 9 8 5 13 12 11 17 18 4 27 21 15 16 23 22 14 20 38 25 24 41 29 32 37 39 36 28 35 30 31 33 26 40 34 
3 4 5 21 9 1 2 11 10 7 8 0 13 12 18 19 20 6 22 16 17 24 23 15 31 27 26 25 29 32 33 39 30 28 41 34 35 36 14 37 38 40 
4 5 6 7 16 11 3 12 2 10 9 8 0 13 19 20 21 15 1 24 18 25 17 35 22 14 27 26 32 33 39 36 28 34 29 40 41 23 30 31 37 38 
5 6 7 1 2 18 13 4 12 11 10 9 8 0 20 21 15 16 17 3 26 19 40 24 23 22 14 27 33 39 36 28 41 29 38 32 25 34 35 30 31 37 
8 7 1 2 3 4 20 0 13 12 11 10 9 6 14 15 16 17 18 19 5 37 26 25 24 23 22 21 31 36 28 41 29 32 33 27 38 40 34 35 30 39 
0 8 9 10 11 12 4 26 3 2 1 7 6 5 27 14 22 23 24 25 32 13 18 17 16 15 21 20 37 31 30 35 34 40 19 38 29 41 28 36 39 33 
13 0 8 9 10 2 12 3 24 1 7 6 5 4 26 27 14 22 23 41 25 18 11 16 15 21 20 19 38 37 31 30 35 17 40 29 34 28 36 39 33 32 
12 13 0 8 7 10 11 2 1 22 6 5 4 3 25 26 27 14 36 23 24 17 16 9 21 20 19 18 40 38 37 31 15 35 34 41 28 30 39 33 32 29 
11 12 13 5 8 9 10 1 7 6 27 4 3 2 24 25 26 33 14 22 23 16 15 21 0 19 18 17 34 40 38 20 31 30 35 28 36 39 37 32 29 41 
10 11 3 13 0 8 9 7 6 5 4 25 2 1 23 24 29 26 27 14 22 15 21 20 19 12 17 16 35 34 18 38 37 31 30 36 39 33 32 40 41 28 
9 1 11 12 13 0 8 6 5 4 3 2 23 7 22 28 24 25 26 27 14 21 20 19 18 17 10 15 30 16 34 40 38 37 31 39 33 32 29 41 35 36 
6 9 10 11 12 13 0 5 4 3 2 1 7 14 39 22 23 24 25 26 27 20 19 18 17 16 15 8 21 30 35 34 40 38 37 33 32 29 41 28 36 31 
21 15 22 16 23 24 18 19 25 20 39 14 26 17 29 37 31 32 33 34 35 28 41 40 27 11 30 36 5 12 13 6 7 9 8 3 4 10 1 38 0 2 
26 22 27 23 24 35 21 17 19 25 20 16 14 15 30 31 39 7 34 18 29 36 28 41 40 32 38 37 0 13 1 33 9 8 5 2 3 4 10 6 11 12 
22 16 23 25 18 21 26 15 17 19 24 20 27 38 31 32 33 41 35 29 30 12 36 28 34 40 39 14 13 6 7 4 8 5 0 37 2 3 9 10 1 11 
16 23 24 18 17 26 22 14 15 21 19 41 20 27 32 33 34 35 2 30 31 38 37 29 28 25 40 39 6 7 9 8 36 0 13 11 12 5 3 4 10 1 
23 24 18 29 26 14 16 27 22 15 17 19 25 20 33 34 35 21 30 38 6 39 31 37 36 28 41 40 7 9 8 5 0 11 32 1 13 12 2 3 4 10 
24 18 21 26 22 16 40 23 27 14 15 17 19 25 34 35 5 30 31 32 20 33 39 38 37 36 28 41 9 8 29 0 13 6 10 7 1 11 12 2 3 4 
19 21 26 22 32 23 24 25 20 27 14 15 17 18 28 29 30 31 16 33 34 41 10 39 38 37 36 35 3 5 0 13 6 7 9 4 40 1 11 12 2 8 
25 19 17 15 14 27 23 20 16 31 26 21 18 24 41 3 36 37 38 39 33 40 32 22 30 29 35 34 4 28 2 12 11 1 7 10 6 13 0 5 8 9 
20 25 28 17 15 22 27 16 14 26 21 18 24 23 40 41 19 36 37 31 39 32 38 30 29 35 9 33 10 4 3 2 12 13 1 6 11 0 5 8 34 7 
27 20 25 19 21 15 14 22 26 17 18 24 33 16 1 40 41 28 29 37 38 31 30 36 35 34 23 32 39 10 4 3 5 12 11 13 0 2 8 9 7 6 
14 27 20 24 19 17 15 30 21 18 25 23 16 22 38 39 40 34 28 36 37 26 29 8 41 33 32 31 11 1 10 9 3 2 12 0 5 35 4 7 6 13 
37 14 16 20 25 19 17 21 18 24 23 27 22 26 15 38 32 40 41 28 36 29 35 34 33 39 31 0 12 11 6 10 4 3 2 5 8 9 7 1 13 30 
17 26 14 27 20 25 19 18 34 23 16 22 15 21 36 30 38 39 40 4 28 35 24 33 32 31 37 29 2 0 11 1 10 41 3 8 9 7 6 13 12 5 
18 36 15 14 27 20 25 24 23 16 22 26 21 19 35 17 37 38 39 40 41 34 33 32 13 30 29 28 8 2 12 11 1 10 4 9 7 6 31 0 5 3 
32 31 35 28 40 29 37 39 30 41 34 33 36 8 21 9 3 4 5 6 7 0 13 12 11 10 2 38 1 24 16 17 18 19 20 22 14 27 26 25 15 23 
36 35 34 40 29 37 32 38 39 30 41 28 10 31 2 16 11 5 6 7 1 8 0 13 12 4 33 9 15 3 26 18 19 20 21 23 22 14 27 17 25 24 
35 28 40 30 37 32 36 31 38 39 29 12 34 33 3 4 18 13 7 1 2 9 8 0 6 41 11 10 16 17 5 14 20 21 15 24 23 22 19 27 26 25 
28 40 29 37 38 36 35 33 31 32 0 30 41 34 4 5 6 20 8 2 3 10 9 1 39 13 12 11 17 18 19 7 23 15 16 25 24 21 22 14 27 26 
40 29 37 32 36 33 28 34 35 9 38 39 30 41 5 6 7 1 15 10 4 11 3 31 8 0 13 12 18 19 20 21 2 25 17 26 16 24 23 22 14 27 
29 37 32 36 35 28 41 40 11 33 31 38 39 30 6 7 1 2 3 17 12 5 34 10 9 8 0 13 19 20 21 15 16 4 27 18 26 25 24 23 22 14 
39 32 36 35 28 40 29 13 41 34 33 31 38 37 0 1 2 3 4 5 19 30 12 11 10 9 8 7 22 21 15 16 17 18 6 14 27 26 25 24 23 20 
30 39 38 31 33 34 5 41 28 35 36 32 37 29 13 0 8 9 10 11 40 27 4 3 2 1 7 6 14 22 23 24 25 26 18 12 17 16 15 21 20 19 
41 30 39 38 31 3 34 28 33 36 32 37 29 40 12 13 0 8 9 35 11 4 25 2 1 7 6 5 27 14 22 23 24 16 26 17 10 15 21 20 19 18 
34 41 30 39 1 31 33 35 36 38 37 29 40 28 11 12 13 0 32 9 10 3 2 23 7 6 5 4 26 27 14 22 21 24 25 16 15 8 20 19 18 17 
33 34 41 6 39 38 31 36 32 37 30 40 28 35 10 11 12 29 0 8 9 2 1 7 14 5 4 3 25 26 27 19 22 23 24 15 21 20 13 18 17 16 
31 33 4 41 30 39 38 32 37 29 40 34 35 36 9 10 28 12 13 0 8 1 7 6 5 26 3 2 24 25 17 27 14 22 23 21 20 19 18 11 16 15 
38 2 33 34 41 30 39 37 29 40 28 35 31 32 8 36 10 11 12 13 0 7 6 5 4 3 24 1 23 15 25 26 27 14 22 20 19 18 17 16 9 21 
7 38 31 33 34 41 30 29 40 28 35 36 32 39 37 8 9 10 11 12 13 6 5 4 3 2 1 22 20 23 24 25 26 27 14 19 18 17 16 15 21 0 

28 7 11 8 5 6 3 4 1 2 9 12 0 10 13 29 30 31 32 33 34 35 36 37 38 39 40 22 27 26 15 21 25 16 18 14 23 19 17 20 24 41 
8 34 13 6 9 5 10 2 11 4 0 7 1 12 31 3 28 33 38 32 41 37 30 35 40 29 23 39 21 18 27 16 17 25 22 19 15 14 24 26 36 20 
1 13 38 12 0 2 6 11 5 10 8 3 4 7 36 28 9 39 40 37 33 30 32 41 31 18 35 29 23 27 17 20 24 19 16 15 25 22 21 34 14 26 
2 4 1 29 3 9 12 10 0 11 13 6 5 8 37 35 36 7 34 38 39 41 40 30 27 33 32 31 19 14 23 26 18 17 20 22 24 15 28 16 25 21 
3 2 10 4 30 13 1 12 9 5 7 0 8 6 34 37 41 35 11 28 36 39 38 25 29 40 31 33 18 19 22 14 15 27 23 20 17 32 26 24 21 16 
12 1 8 5 10 35 13 0 2 9 6 11 7 3 39 36 31 32 41 4 28 40 19 38 33 30 29 34 20 23 21 25 22 14 27 24 37 17 16 15 26 18 
6 5 7 2 12 10 40 9 4 1 3 8 13 11 33 32 29 37 39 41 0 17 35 36 34 31 28 30 16 25 26 19 20 22 24 38 14 23 18 21 27 15 
11 9 6 13 2 3 7 31 10 0 4 1 12 5 30 38 33 28 37 34 26 8 41 40 35 36 39 32 15 17 16 27 19 18 29 21 22 24 14 23 20 25 
7 0 2 1 4 8 11 5 33 3 12 9 10 13 29 40 37 36 35 21 30 32 6 34 39 38 41 28 26 24 19 23 14 31 15 25 16 18 20 17 22 27 
0 10 5 3 6 1 8 7 13 39 2 4 11 9 40 41 32 34 16 36 31 29 28 12 37 35 30 38 24 22 25 18 33 23 21 26 27 20 19 14 15 17 
5 6 12 11 8 0 9 1 7 13 41 2 3 4 32 33 39 15 31 40 38 36 29 28 10 37 34 35 25 16 20 30 21 24 17 23 26 27 22 19 18 14 
10 11 0 9 13 12 4 3 8 7 1 32 6 2 41 30 24 38 28 39 35 34 31 29 36 5 33 37 22 15 40 17 27 20 14 18 21 26 23 25 16 19 
9 12 4 10 1 7 5 6 3 8 11 13 37 0 38 20 35 41 36 29 32 33 34 31 30 28 2 40 17 39 14 22 23 26 25 16 18 21 15 27 19 24 
4 8 3 0 7 11 2 13 12 6 5 10 9 36 14 31 34 40 29 30 37 28 39 33 32 41 38 1 35 21 18 24 26 15 19 27 20 16 25 22 17 23 
15 27 22 25 17 20 23 16 24 26 10 19 18 21 0 1 2 3 4 5 6 7 8 9 14 34 12 13 32 31 38 40 28 30 33 37 29 41 39 11 35 36 
25 23 15 20 14 4 21 26 22 16 18 27 24 19 3 6 0 30 10 17 13 9 2 7 12 1 8 11 40 33 32 5 39 28 36 41 38 37 35 31 29 34 
24 15 14 19 18 26 20 22 17 21 25 23 16 1 8 0 10 11 12 9 5 38 4 13 3 6 7 27 29 32 39 34 35 41 30 2 28 36 40 33 37 31 
26 16 24 27 23 14 19 21 18 22 15 5 17 25 9 7 8 1 33 10 11 13 12 2 0 20 4 3 41 37 29 31 6 39 34 36 35 38 32 30 28 40 
23 26 21 7 22 15 24 19 14 17 27 18 25 20 6 9 13 16 2 0 29 11 10 4 1 12 3 5 33 41 36 37 38 32 8 34 39 28 31 35 40 30 
19 24 25 17 21 16 0 18 26 14 20 22 27 23 11 8 40 4 13 7 15 12 9 10 5 2 1 6 34 29 3 28 36 37 32 35 41 39 30 38 31 33 
20 17 27 26 11 21 18 14 16 24 23 25 15 22 5 4 1 9 19 13 12 10 37 8 6 3 0 2 30 28 31 41 34 36 35 39 7 29 33 40 32 38 
22 14 20 15 26 23 27 25 21 12 16 24 19 17 2 39 5 0 9 6 1 3 13 18 7 8 11 4 38 10 30 32 41 33 31 40 36 35 37 29 34 28 
27 18 9 24 16 25 22 17 20 23 19 14 21 15 1 12 26 8 7 3 2 4 5 6 11 10 36 0 31 35 41 29 37 40 38 28 30 33 34 39 13 32 
18 21 17 23 20 24 25 27 15 19 26 16 2 14 35 13 4 6 5 8 3 1 0 11 9 7 22 10 12 36 28 33 30 29 40 31 32 34 41 37 38 39 
17 20 19 22 25 18 14 8 27 15 21 26 23 16 4 5 11 2 3 12 10 24 1 32 13 9 6 7 28 30 34 38 40 35 39 29 31 0 36 41 33 37 
13 22 18 14 15 19 16 23 25 27 24 17 20 26 21 2 12 10 0 11 7 6 3 1 8 4 5 41 36 38 35 39 32 34 37 33 40 31 29 28 30 9 
14 19 16 21 24 27 17 20 6 25 22 15 26 18 10 11 7 13 8 31 4 5 23 3 2 0 9 12 39 34 37 36 29 1 28 30 33 40 38 32 41 35 
16 3 23 18 27 22 26 15 19 20 17 21 14 24 7 25 6 12 1 2 9 0 11 5 28 13 10 8 37 40 33 35 31 38 41 32 34 30 4 36 39 29 
41 40 29 35 39 30 32 28 37 33 31 34 38 27 12 15 16 17 18 19 20 21 22 23 24 25 26 36 14 5 6 2 11 7 10 1 9 13 3 0 8 4 
35 32 41 30 31 39 36 33 29 28 38 40 22 34 17 10 14 19 24 18 27 23 16 21 26 15 37 25 2 20 12 7 3 11 4 13 6 1 8 5 9 0 
37 41 31 34 38 33 30 29 39 36 35 20 28 40 22 14 3 25 26 23 19 16 18 27 17 32 21 15 9 12 24 0 8 13 7 6 11 4 2 10 1 5 
33 28 37 40 32 31 34 36 38 29 14 30 39 35 23 21 22 5 20 24 25 27 26 16 41 19 18 17 13 1 9 15 10 3 0 4 8 6 12 7 11 2 
32 33 36 28 29 41 37 34 31 18 40 38 35 30 20 23 27 21 6 14 22 25 24 39 15 26 17 19 10 13 4 1 16 12 9 0 3 11 5 8 2 7 
34 37 35 39 36 28 41 38 23 31 30 29 40 32 25 22 17 18 27 1 14 26 33 24 19 16 15 20 0 9 2 11 4 21 12 8 13 3 7 6 5 10 
30 39 40 33 34 36 38 24 28 37 32 35 41 29 19 18 15 23 25 27 8 31 21 22 20 17 14 16 7 11 5 13 0 4 26 3 1 9 10 2 12 6 
29 31 30 41 33 32 15 35 36 38 28 37 34 39 16 24 19 14 23 20 40 2 27 26 21 22 25 18 6 3 7 12 13 10 5 17 4 8 1 9 0 11 
40 38 33 37 28 17 29 39 30 32 34 31 36 41 15 26 23 22 21 35 16 18 7 20 25 24 27 14 5 8 13 9 1 2 6 11 19 10 0 3 4 12 
38 36 39 32 19 37 35 40 41 34 33 28 29 31 26 27 18 20 30 22 17 15 14 0 23 21 16 24 8 4 11 10 7 9 2 5 12 25 13 1 6 3 
39 30 34 16 35 38 31 37 40 41 36 33 32 28 18 19 25 29 17 26 24 22 15 14 4 23 20 21 11 7 0 6 2 8 3 9 5 12 27 13 10 1 
36 29 26 31 41 34 28 32 35 40 37 39 30 33 27 16 38 24 14 25 21 20 17 15 22 11 19 23 4 6 8 3 12 0 1 10 2 5 9 18 7 13 
31 25 28 36 37 40 39 30 32 35 29 41 33 38 24 34 21 27 22 15 18 19 20 17 16 14 13 26 3 0 1 4 9 5 11 7 10 2 6 12 23 8 
21 35 32 38 40 29 33 41 34 30 39 36 31 37 28 17 20 26 15 16 23 14 25 19 18 27 24 9 1 2 10 8 5 6 13 12 0 7 11 4 3 22

Утилита Harry White подтверждает ортогональность этих ДЛК

Order? 42

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_5.txt

Counts
------
         2 diagonal Latin
         1 orthogonal pair

Итак, закрыли ещё один проблемный порядок.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Порядки 43, 44, 45 не проблемные.
Порядок 46 проблемный.
Одиночный ДЛК 46-го порядка можно построить методом Гергели по моей программке для порядков n=2k, k - нечётное число не кратное 3.
Сейчас попробую.
Ну, а как построить ортогональную пару ДЛК данного порядка, пока не знаю.
Надо будет искать ортогональные диагональные соквадраты к ДЛК, построенному методом Гергели. Может быть, они у него есть.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

ДЛК 46-го порядка, построенный методом Гергели

1 25 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 0 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 2 24 
2 3 27 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 24 0 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 4 26 25 
3 4 5 29 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 25 24 0 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 6 28 27 26 
4 5 6 7 31 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 26 25 24 0 45 44 43 42 41 40 39 38 37 36 35 34 33 32 8 30 29 28 27 
5 6 7 8 9 33 11 12 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 27 26 25 24 0 45 44 43 42 41 40 39 38 37 36 35 34 10 32 31 30 29 28 
6 7 8 9 10 11 35 13 14 15 16 17 18 19 20 21 22 23 1 2 3 4 5 28 27 26 25 24 0 45 44 43 42 41 40 39 38 37 36 12 34 33 32 31 30 29 
7 8 9 10 11 12 13 37 15 16 17 18 19 20 21 22 23 1 2 3 4 5 6 29 28 27 26 25 24 0 45 44 43 42 41 40 39 38 14 36 35 34 33 32 31 30 
8 9 10 11 12 13 14 15 39 17 18 19 20 21 22 23 1 2 3 4 5 6 7 30 29 28 27 26 25 24 0 45 44 43 42 41 40 16 38 37 36 35 34 33 32 31 
9 10 11 12 13 14 15 16 17 41 19 20 21 22 23 1 2 3 4 5 6 7 8 31 30 29 28 27 26 25 24 0 45 44 43 42 18 40 39 38 37 36 35 34 33 32 
10 11 12 13 14 15 16 17 18 19 43 21 22 23 1 2 3 4 5 6 7 8 9 32 31 30 29 28 27 26 25 24 0 45 44 20 42 41 40 39 38 37 36 35 34 33 
11 12 13 14 15 16 17 18 19 20 21 45 23 1 2 3 4 5 6 7 8 9 10 33 32 31 30 29 28 27 26 25 24 0 22 44 43 42 41 40 39 38 37 36 35 34 
12 13 14 15 16 17 18 19 20 21 22 23 24 2 3 4 5 6 7 8 9 10 11 34 33 32 31 30 29 28 27 26 25 1 0 45 44 43 42 41 40 39 38 37 36 35 
13 14 15 16 17 18 19 20 21 22 23 1 2 26 4 5 6 7 8 9 10 11 12 35 34 33 32 31 30 29 28 27 3 25 24 0 45 44 43 42 41 40 39 38 37 36 
14 15 16 17 18 19 20 21 22 23 1 2 3 4 28 6 7 8 9 10 11 12 13 36 35 34 33 32 31 30 29 5 27 26 25 24 0 45 44 43 42 41 40 39 38 37 
15 16 17 18 19 20 21 22 23 1 2 3 4 5 6 30 8 9 10 11 12 13 14 37 36 35 34 33 32 31 7 29 28 27 26 25 24 0 45 44 43 42 41 40 39 38 
16 17 18 19 20 21 22 23 1 2 3 4 5 6 7 8 32 10 11 12 13 14 15 38 37 36 35 34 33 9 31 30 29 28 27 26 25 24 0 45 44 43 42 41 40 39 
17 18 19 20 21 22 23 1 2 3 4 5 6 7 8 9 10 34 12 13 14 15 16 39 38 37 36 35 11 33 32 31 30 29 28 27 26 25 24 0 45 44 43 42 41 40 
18 19 20 21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 36 14 15 16 17 40 39 38 37 13 35 34 33 32 31 30 29 28 27 26 25 24 0 45 44 43 42 41 
19 20 21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 38 16 17 18 41 40 39 15 37 36 35 34 33 32 31 30 29 28 27 26 25 24 0 45 44 43 42 
20 21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 40 18 19 42 41 17 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 0 45 44 43 
21 22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 42 20 43 19 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 0 45 44 
22 23 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 44 21 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 0 45 
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 45 44 43 42 41 40 39 38 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 
45 0 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 21 44 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 23 22 
44 45 0 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 19 43 20 42 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 23 22 21 
43 44 45 0 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 17 41 42 19 18 40 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 23 22 21 20 
42 43 44 45 0 24 25 26 27 28 29 30 31 32 33 34 35 36 37 15 39 40 41 18 17 16 38 14 13 12 11 10 9 8 7 6 5 4 3 2 1 23 22 21 20 19 
41 42 43 44 45 0 24 25 26 27 28 29 30 31 32 33 34 35 13 37 38 39 40 17 16 15 14 36 12 11 10 9 8 7 6 5 4 3 2 1 23 22 21 20 19 18 
40 41 42 43 44 45 0 24 25 26 27 28 29 30 31 32 33 11 35 36 37 38 39 16 15 14 13 12 34 10 9 8 7 6 5 4 3 2 1 23 22 21 20 19 18 17 
39 40 41 42 43 44 45 0 24 25 26 27 28 29 30 31 9 33 34 35 36 37 38 15 14 13 12 11 10 32 8 7 6 5 4 3 2 1 23 22 21 20 19 18 17 16 
38 39 40 41 42 43 44 45 0 24 25 26 27 28 29 7 31 32 33 34 35 36 37 14 13 12 11 10 9 8 30 6 5 4 3 2 1 23 22 21 20 19 18 17 16 15 
37 38 39 40 41 42 43 44 45 0 24 25 26 27 5 29 30 31 32 33 34 35 36 13 12 11 10 9 8 7 6 28 4 3 2 1 23 22 21 20 19 18 17 16 15 14 
36 37 38 39 40 41 42 43 44 45 0 24 25 3 27 28 29 30 31 32 33 34 35 12 11 10 9 8 7 6 5 4 26 2 1 23 22 21 20 19 18 17 16 15 14 13 
35 36 37 38 39 40 41 42 43 44 45 0 1 25 26 27 28 29 30 31 32 33 34 11 10 9 8 7 6 5 4 3 2 24 23 22 21 20 19 18 17 16 15 14 13 12 
34 35 36 37 38 39 40 41 42 43 44 22 0 24 25 26 27 28 29 30 31 32 33 10 9 8 7 6 5 4 3 2 1 23 45 21 20 19 18 17 16 15 14 13 12 11 
33 34 35 36 37 38 39 40 41 42 20 44 45 0 24 25 26 27 28 29 30 31 32 9 8 7 6 5 4 3 2 1 23 22 21 43 19 18 17 16 15 14 13 12 11 10 
32 33 34 35 36 37 38 39 40 18 42 43 44 45 0 24 25 26 27 28 29 30 31 8 7 6 5 4 3 2 1 23 22 21 20 19 41 17 16 15 14 13 12 11 10 9 
31 32 33 34 35 36 37 38 16 40 41 42 43 44 45 0 24 25 26 27 28 29 30 7 6 5 4 3 2 1 23 22 21 20 19 18 17 39 15 14 13 12 11 10 9 8 
30 31 32 33 34 35 36 14 38 39 40 41 42 43 44 45 0 24 25 26 27 28 29 6 5 4 3 2 1 23 22 21 20 19 18 17 16 15 37 13 12 11 10 9 8 7 
29 30 31 32 33 34 12 36 37 38 39 40 41 42 43 44 45 0 24 25 26 27 28 5 4 3 2 1 23 22 21 20 19 18 17 16 15 14 13 35 11 10 9 8 7 6 
28 29 30 31 32 10 34 35 36 37 38 39 40 41 42 43 44 45 0 24 25 26 27 4 3 2 1 23 22 21 20 19 18 17 16 15 14 13 12 11 33 9 8 7 6 5 
27 28 29 30 8 32 33 34 35 36 37 38 39 40 41 42 43 44 45 0 24 25 26 3 2 1 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 31 7 6 5 4 
26 27 28 6 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 0 24 25 2 1 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 29 5 4 3 
25 26 4 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 0 24 1 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 27 3 2 
24 2 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 0 23 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 25 1 
23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 22 21 20 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Утилита Harry White отметила в этом ДЛК симметричность по Гергели/Брауну.
Будем надеяться, что у этого ДЛК есть орогональные диагональные соквадраты.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Порядки 47, 48, 49, 50 не проблемные.

Тэк-с, полста :)
Пока хватит.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Возвращаюсь назад. Буду разбираться с группами пар ОДЛК для разных порядков n>10.

Сейчас взяла из статьи Чернова
http://alex-black.ru/article.php?content=125
ДЛК 13-го порядка, построенный методом Линдера

 0 1 2 3 4 5 6 7 8 9 10 11 12 
 6 2 1 5 3 4 0 9 7 8 12 10 11 
 1 0 6 4 5 3 2 8 9 7 11 12 10 
 7 8 9 12 1 10 11 2 6 0 3 4 5 
 9 7 8 11 10 1 12 0 2 6 5 3 4 
 8 9 7 1 12 11 10 6 0 2 4 5 3 
 2 6 0 10 11 12 1 3 4 5 7 8 9 
 10 11 12 7 8 9 4 5 1 3 2 6 0 
 12 10 11 9 7 8 5 4 3 1 0 2 6 
 11 12 10 8 9 7 3 1 5 4 6 0 2 
 3 4 5 2 6 0 8 10 11 12 9 1 7 
 5 3 4 0 2 6 9 12 10 11 8 7 1 
 4 5 3 6 0 2 7 11 12 10 1 9 8

и поищу для него ортогональные диагональные соквадраты программой Белышева ortogonal_u.
Я искала ортогональные диагональные соквадраты для ДЛК 13-го порядка, построенного методом Гергели; покрутила немного программу - до первого найденного ОДЛК. Этот ОДЛК показан выше.
Затем искала для одного из ДЛК 13-го порядка из полной системы MOLS, для этого ДЛК нашла 4949 ортогональных ДЛК, но это ещё не все, прервала программу.
Теперь пробую поискать ортогональные диагональные соквадраты для ДЛК 13-го порядка из статьи Чернова.
Пока ДЛК не найдены

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 14151
Соквадратов:     0
Время в сек:     465

685 183 35 29 1

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Кстати, надо посмотреть построение одиночного ДЛК 39-го порядка методом Гергели.
Это единственный проблемный порядок до n=50, для которого у меня нет даже одиночного ДЛК.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Получилось!
ДЛК 39-го порядка, построенный методом Гергели

1 38 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 21 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 2 20
2 3 38 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 1 23 20 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 4 22 21
3 4 5 38 7 8 9 10 11 12 13 14 15 16 17 18 19 1 2 25 21 20 0 37 36 35 34 33 32 31 30 29 28 27 26 6 24 23 22
4 5 6 7 38 9 10 11 12 13 14 15 16 17 18 19 1 2 3 27 22 21 20 0 37 36 35 34 33 32 31 30 29 28 8 26 25 24 23
5 6 7 8 9 38 11 12 13 14 15 16 17 18 19 1 2 3 4 29 23 22 21 20 0 37 36 35 34 33 32 31 30 10 28 27 26 25 24
6 7 8 9 10 11 38 13 14 15 16 17 18 19 1 2 3 4 5 31 24 23 22 21 20 0 37 36 35 34 33 32 12 30 29 28 27 26 25
7 8 9 10 11 12 13 38 15 16 17 18 19 1 2 3 4 5 6 33 25 24 23 22 21 20 0 37 36 35 34 14 32 31 30 29 28 27 26
8 9 10 11 12 13 14 15 38 17 18 19 1 2 3 4 5 6 7 35 26 25 24 23 22 21 20 0 37 36 16 34 33 32 31 30 29 28 27
9 10 11 12 13 14 15 16 17 38 19 1 2 3 4 5 6 7 8 37 27 26 25 24 23 22 21 20 0 18 36 35 34 33 32 31 30 29 28
10 11 12 13 14 15 16 17 18 19 38 2 3 4 5 6 7 8 9 20 28 27 26 25 24 23 22 21 1 0 37 36 35 34 33 32 31 30 29
11 12 13 14 15 16 17 18 19 1 2 38 4 5 6 7 8 9 10 22 29 28 27 26 25 24 23 3 21 20 0 37 36 35 34 33 32 31 30
12 13 14 15 16 17 18 19 1 2 3 4 38 6 7 8 9 10 11 24 30 29 28 27 26 25 5 23 22 21 20 0 37 36 35 34 33 32 31
13 14 15 16 17 18 19 1 2 3 4 5 6 38 8 9 10 11 12 26 31 30 29 28 27 7 25 24 23 22 21 20 0 37 36 35 34 33 32
14 15 16 17 18 19 1 2 3 4 5 6 7 8 38 10 11 12 13 28 32 31 30 29 9 27 26 25 24 23 22 21 20 0 37 36 35 34 33
15 16 17 18 19 1 2 3 4 5 6 7 8 9 10 38 12 13 14 30 33 32 31 11 29 28 27 26 25 24 23 22 21 20 0 37 36 35 34
16 17 18 19 1 2 3 4 5 6 7 8 9 10 11 12 38 14 15 32 34 33 13 31 30 29 28 27 26 25 24 23 22 21 20 0 37 36 35
17 18 19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 38 16 34 35 15 33 32 31 30 29 28 27 26 25 24 23 22 21 20 0 37 36
18 19 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 38 36 17 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 0 37
38 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 37 36 35 34 33 32 31 30 29 28 27 26 25 24 23 22 21 20 19
0 21 23 25 27 29 31 33 35 37 20 22 24 26 28 30 32 34 36 38 18 16 14 12 10 8 6 4 2 19 17 15 13 11 9 7 5 3 1
37 0 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 17 16 36 38 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 19 18
36 37 0 20 21 22 23 24 25 26 27 28 29 30 31 32 33 15 35 14 16 34 38 13 12 11 10 9 8 7 6 5 4 3 2 1 19 18 17
35 36 37 0 20 21 22 23 24 25 26 27 28 29 30 31 13 33 34 12 15 14 32 38 11 10 9 8 7 6 5 4 3 2 1 19 18 17 16
34 35 36 37 0 20 21 22 23 24 25 26 27 28 29 11 31 32 33 10 14 13 12 30 38 9 8 7 6 5 4 3 2 1 19 18 17 16 15
33 34 35 36 37 0 20 21 22 23 24 25 26 27 9 29 30 31 32 8 13 12 11 10 28 38 7 6 5 4 3 2 1 19 18 17 16 15 14
32 33 34 35 36 37 0 20 21 22 23 24 25 7 27 28 29 30 31 6 12 11 10 9 8 26 38 5 4 3 2 1 19 18 17 16 15 14 13
31 32 33 34 35 36 37 0 20 21 22 23 5 25 26 27 28 29 30 4 11 10 9 8 7 6 24 38 3 2 1 19 18 17 16 15 14 13 12
30 31 32 33 34 35 36 37 0 20 21 3 23 24 25 26 27 28 29 2 10 9 8 7 6 5 4 22 38 1 19 18 17 16 15 14 13 12 11
29 30 31 32 33 34 35 36 37 0 1 21 22 23 24 25 26 27 28 19 9 8 7 6 5 4 3 2 20 38 18 17 16 15 14 13 12 11 10
28 29 30 31 32 33 34 35 36 18 0 20 21 22 23 24 25 26 27 17 8 7 6 5 4 3 2 1 19 37 38 16 15 14 13 12 11 10 9
27 28 29 30 31 32 33 34 16 36 37 0 20 21 22 23 24 25 26 15 7 6 5 4 3 2 1 19 18 17 35 38 14 13 12 11 10 9 8
26 27 28 29 30 31 32 14 34 35 36 37 0 20 21 22 23 24 25 13 6 5 4 3 2 1 19 18 17 16 15 33 38 12 11 10 9 8 7
25 26 27 28 29 30 12 32 33 34 35 36 37 0 20 21 22 23 24 11 5 4 3 2 1 19 18 17 16 15 14 13 31 38 10 9 8 7 6
24 25 26 27 28 10 30 31 32 33 34 35 36 37 0 20 21 22 23 9 4 3 2 1 19 18 17 16 15 14 13 12 11 29 38 8 7 6 5
23 24 25 26 8 28 29 30 31 32 33 34 35 36 37 0 20 21 22 7 3 2 1 19 18 17 16 15 14 13 12 11 10 9 27 38 6 5 4
22 23 24 6 26 27 28 29 30 31 32 33 34 35 36 37 0 20 21 5 2 1 19 18 17 16 15 14 13 12 11 10 9 8 7 25 38 4 3
21 22 4 24 25 26 27 28 29 30 31 32 33 34 35 36 37 0 20 3 1 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 23 38 2
20 2 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 0 1 19 18 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 21 38
19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 18 38 17 16 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0

Утилита Harry White подтверждает, что это диагональный латинский квадрат

Order? 39

Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_2.txt

Counts
------
         1 diagonal Latin

Никаких свойств в этом ДЛК утилита не отмечает.
Ну и... как всегда вопрос: как найти ортогональные ДЛК к данному ДЛК, ежели они у него есть?

Теперь для всех проблемных порядков до n=50 одиночные ДЛК построены.
Осталось построить ортогональные пары ДЛК.
Напомню проблемные порядки до n=50, которые у нас пока без ортогональных пар ДЛК: 21, 33, 38, 39 и 46.
Для порядков 21 и 33 есть надежда на метод Линдера.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Проверка ДЛК 13-го порядка из статьи Чернова ничего не дала

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 14151
Соквадратов:     0
Время в сек:     4175

668 199 1 23 5  1

Больше часа работала и не нашла ни одного соквадрата!
Прервала программу.

Кстати, очень мало диагональных трансверсалей у этого ДЛК (14151).
Сравните с ДЛК из полной системы MOLS

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 131106
Соквадратов:     4937
Время в сек:     10270

9114 4110 1558 230 24 16  6

А это у ДЛК, построенного методом Гергели

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 12034
Соквадратов:     1
Время в сек:     8380

710 122 98 12 1 2

У этого ДЛК тоже мало диагональных трансверсалей, вот и нашёлся пока только один ортогональный диагональный соквадрат.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Цитата

Проверка ДЛК 13-го порядка из статьи Чернова ничего не дала

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 14151
Соквадратов:     0
Время в сек:     4175

668 199 1 23 5  1

Больше часа работала и не нашла ни одного соквадрата!
Прервала программу.

Ой, заработалась и забыла прервать программу :)
Как хорошо!
Ортогональный диагональный соквадрат нашёлся!

Проверка ДЛК13 на марьяжность (ОДЛК)

Введено ДЛК:     1
Найдено ОДЛК:    0

Д-трансверсалей: 14151
Соквадратов:     1
Время в сек:     7475

656 131 55 11 3 1

Ну вот и отлично. Квадратик, найденный методом Линдера, имеет ортогональный диагональный соквадрат.
Вот он

8 3 0 9 A B 6 1 7 4 2 C 5
3 4 2 A 6 5 0 C B 8 1 7 9
C 1 5 2 4 0 7 B 3 9 A 8 6
7 2 B C 1 4 5 A 8 6 3 9 0
2 5 6 1 0 A 4 3 9 7 8 B C
A 0 4 8 3 6 9 2 C 5 B 1 7
1 A 9 3 2 7 B 5 4 C 6 0 8
5 8 A 0 9 1 3 7 6 2 C 4 B
9 B 7 5 8 C 2 6 A 0 4 3 1
B 6 C 4 7 3 8 9 5 1 0 A 2
4 7 3 6 C 2 1 8 0 B 9 5 A
6 C 8 7 B 9 A 0 1 3 5 2 4
0 9 1 B 5 8 C 4 2 A 7 6 3

Теперь уже точно прервала программу, черепашка пойдёт отдыхать.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Поискала в Интернете статью о методе Линдера
Charles C.Linder. Construction Of Doubly Diagonalized Orthogonal Latin Squares
Вот ссылка
https://www.semanticscholar.org/paper/Construction-of-doubly-diagonalized-orthogonal-Lindner/c80a7d3554aaedf4402ce0d242ca328ae8dc615e
которая привела сюда

• DOI:10.1016/0012-365X(73)90028-9
Corpus ID: 11352073
Construction of doubly diagonalized orthogonal latin squares
@article{Lindner1973ConstructionOD,
title={Construction of doubly diagonalized orthogonal latin squares},
author={Charles C. Lindner},
journal={Discret. Math.},
year={1973},
volume={5},
pages={79-86}
}
• Charles C. Lindner
• Published 1973
• Mathematics, Computer Science
• Discret. Math.
A transversal T of a latin square is a collection of n cells no two in the same row or column and such that each of the integers 1, 2, ..., n appears in exactly one of the cells of T. A latin square is doubly diagonalized provided that both its main diagonal and off-diagonal are transversals. Although it is known that a doubly diagonalized latin square of every order n >= 4 exists and that a pair of orthogonal latin squares of order n exists for every n 2 or 6, it is still an open question as… CONTINUE READING

На этой странице куда-то нажала, такая ссылка получилась
https://www.sciencedirect.com/science/article/pii/0012365X73900289?via%3Dihub

На этой странице куда-то нажала, получила пятикилометровую ссылку (не буду постить), которая открывает статью в PDF.
В общем, статья есть. Надо только разобраться.
Мне это очень трудно; надо, во-первых, переводить статью на русский язык, так как я по-английски не читаю.

Алексею Чернову написала письмо с просьбой помочь разобраться, но получить ответ нет никакой надежды.
Алексей давно завязал с квадратами.
Его тёзка - Алексей Белышев, похоже, тоже завязал :)
Сергей Беляев давно бросил заниматься квадратами.
Владимир Чирков - туда же.
Мужчины! Как же вы могли устать вперёд слабой женщины? :)

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Интернет у нас с черепашкой о-ч-е-н-ь плохо работает.
Ну, черепашка на это не обращает никакого внимания и отлично работает.
Я тоже стараюсь работать, но у меня плохо получается, потому что нервничаю из-за Интернета.
Вот сейчас буду отправлять сообщение, нажимаю кнопку "Отправить" и держу её нажатой... иначе никак.
В результате тут может оказаться 3, 4, 5... постов. Потом начинаю их удалять. Удалить тоже не сразу получается - с 10-й попытки.
Вот так и работаю.
Работу Интернета наладить пытаемся, но пока всё глухо.

Итак, у нас нет ортогональной пары ДЛК 21-го порядка.
И я попыталась сконструировать её по аналогии с построениями по квази-разностной матрице.
Но сейчас у меня не было готовой квази-разностной матрицы.
Я взяла ДЛК 17-го порядка (он был изначальный белый), пристроила к нему подквадрат 4х4, он в правом нижнем углу.
Ну, а дальше технология как по квази-разностной матрице.
В своё время я много строила по квази-разностной матрице, и эта технология у меня как-то подсознательно "записалась".
К сожалению, ДЛК не получился, не хватило совсем чуть-чуть; ячейки с нарушением диагональности в побочной диагонали (красная) окрашены коричневым цветом, их всего четыре.
Однако ЛК получился очень даже симпатичный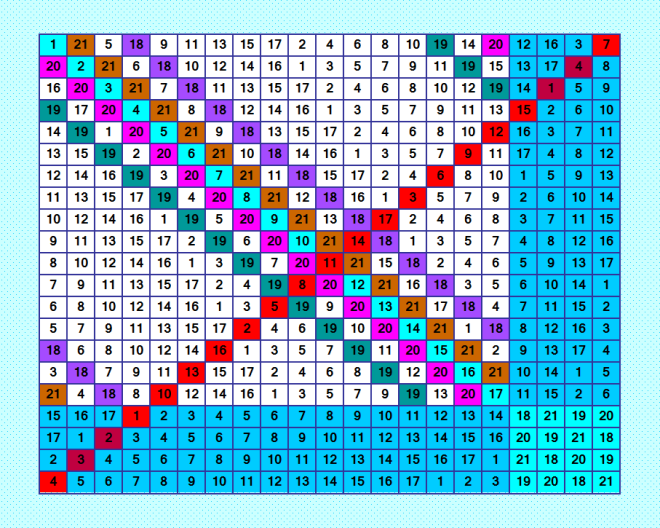



Можно продолжить построение этой группы ЛК, думаю, вполне понятно, как это делать.
Если учесть, что полная система MOLS 4-го порядка состоит из трёх ЛК, можно получить группу MOLS 21-го порядка, состоящую тоже из трёх ЛК.
Но нам не нужна группа взаимно ортогональных ЛК, нам хотя бы одну ортогональную пару ДЛК 21-го порядка построить.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Напомню одиночный ДЛК 21-го порядка, построенный методом Линдера

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 
2 10 3 1 0 6 9 8 5 7 4 12 15 14 11 13 17 20 19 16 18 
4 2 1 10 3 7 8 6 9 5 0 13 14 12 15 11 18 19 17 20 16 
1 3 0 4 10 9 7 5 6 8 2 15 13 11 12 14 20 18 16 17 19 
3 4 10 0 2 8 5 9 7 6 1 14 11 15 13 12 19 16 20 18 17 
11 12 13 14 15 20 17 19 3 18 16 10 1 4 2 0 5 6 7 8 9 
12 15 14 11 13 19 16 3 17 20 18 1 0 2 10 4 6 9 8 5 7 
13 14 12 15 11 18 19 17 16 3 20 4 2 1 0 10 7 8 6 9 5 
15 13 11 12 14 17 3 20 18 16 19 0 4 10 1 2 9 7 5 6 8 
14 11 15 13 12 3 18 16 20 19 17 2 10 0 4 1 8 5 9 7 6 
10 0 4 2 1 16 20 18 19 17 3 5 9 7 8 6 11 15 13 14 12 
16 17 18 19 20 11 12 13 14 15 5 9 6 8 3 7 10 1 4 2 0 
17 20 19 16 18 12 15 14 11 13 7 8 5 3 6 9 1 0 2 10 4 
18 19 17 20 16 13 14 12 15 11 9 7 8 6 5 3 4 2 1 0 10 
20 18 16 17 19 15 13 11 12 14 8 6 3 9 7 5 0 4 10 1 2 
19 16 20 18 17 14 11 15 13 12 6 3 7 5 9 8 2 10 0 4 1 
5 6 7 8 9 10 1 4 2 0 11 16 17 18 19 20 15 12 14 3 13 
6 9 8 5 7 1 0 2 10 4 13 17 20 19 16 18 14 11 3 12 15 
7 8 6 9 5 4 2 1 0 10 15 18 19 17 20 16 13 14 12 11 3 
9 7 5 6 8 0 4 10 1 2 14 20 18 16 17 19 12 3 15 13 11 
8 5 9 7 6 2 10 0 4 1 12 19 16 20 18 17 3 13 11 15 14

Здесь тоже есть какие-то подквадраты. Надо раскрасить их.
Думаю, что ортогональный ДЛК к этому ДЛК построить можно и даже совсем не сложно.
Надо немножко вникнуть в статью о методе Линдера.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg

Раскрасила ДЛК 21-го порядка, построенный методом Линдера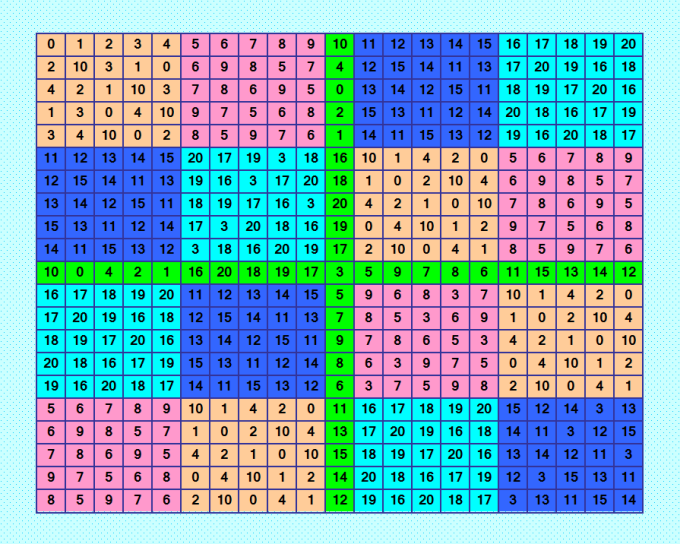



Напомню, что командная строка для построения этого ДЛК мной использовалась такая

test 4 1 6

где 4 - порядок квадрата V, 1 - порядок квадрата P, 6 - порядок квадрата Q.

Ещё важно видеть вспомогательные квадраты, которые построила программа

V = 
 1  3  4  2 
 4  2  1  3 
 2  4  3  1 
 3  1  2  4 
Q = 
 1  3  2  5  6  4 
 3  2  4  6  1  5 
 5  6  3  1  4  2 
 2  5  6  4  3  1 
 6  4  1  2  5  3 
 4  1  5  3  2  6 
P1 = 
 3  4  5  6  2 
 4  2  6  3  5 
 5  6  4  2  3 
 2  5  3  4  6 
 6  3  2  5  4

О квадратах V, P, Q, P1 сказано следующее:
квадрат V - ДЛК чётного порядка;
квадрат P - ДЛК;
квадрат Q - не ДЛК, только главная диагональ содержит разные элементы;
квадрат P1 - не ДЛК, только побочная диагональ содержит разные элементы.
В приведённом примере всё так и есть.

Осталось совсем чуть-чуть: разобраться, как составляются все подквадраты, и составить ортогональные к ним.

---

My new article "SOLS and SODLS"
in Russian https://yadi.sk/d/nvdI6TgBrKv72A
in English https://yadi.sk/d/VeY9bx6_q6CcZg