ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
Previous · 1 · 2 · 3 · 4 · 5 · 6 . . . 27 · Next
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ГРУППЫ ВЗАИМНО ОРТОГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ Mutually Orthogonal Latin squares (MOLS) http://www.natalimak1.narod.ru/grolk.htm Цитирую Напомню, что группа из m латинских квадратов порядка n называется группой (или системой) взаимно (или попарно) ортогональных квадратов, если любые два квадрата этой группы ортогональны. Ссылка на ресурс, где была таблица для Q(n), сейчас не работает. Интересно: есть ли другой ресурс с этой таблицей. Если кто найдёт, сообщите, пожалуйста. Может, что-то новое уже найдено математиками даже для порядков до n=20. Обратите внимание на это Далее доказано, что для любого порядка n, являющегося простым числом или степенью простого числа, существует ровно n-1 взаимно ортогональных квадратов. Порядок 16 является степенью простого числа 2, значит, для него существует полная система MOLS, состоящая из 15 ЛК. Вот и отлично. Вы можете построить эту полную систему MOLS в матпакете Maple. Здесь можете показать, если построите. Я в те давние времена, когда занималась ЛК, построила одну ортогональную пару ДЛК 16-го порядка по аналогии с ортогональной парой ДЛК 8-го порядка. Позже покажу эту ортогональную пару. А пока начну с ДЛК 16-го порядка, построенного методом Гергели. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это ДЛК 16-го порядка, построенный методом Гергели в моей статье ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/dlk.htm 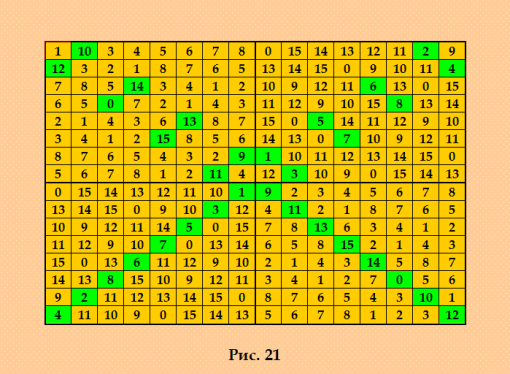 Проверка ДЛК утилитой Harry White Tuesday 2020-06-09 19:05:41 ╠юёъютёъюх тЁхь (чшьр)
Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
1 diagonal Latin
1 axial symmetricОтмечена симметричность по Гергели/Брауну. Поиск ортогональных диагональных соквадратов к этому ДЛК не увенчался успехом; программа Белышева ругается, что слишком много диагональных трансверсалей Число диагональных трансверсалей ДЛК16: 1 A 3 4 5 6 7 8 0 F E D C B 2 9 C 3 2 1 8 7 6 5 D E F 0 9 A B 4 7 8 5 E 3 4 1 2 A 9 C B 6 D 0 F 6 5 0 7 2 1 4 3 B C 9 A F 8 D E 2 1 4 3 6 D 8 7 F 0 5 E B C 9 A 3 4 1 2 F 8 5 6 E D 0 7 A 9 C B 8 7 6 5 4 3 2 9 1 A B C D E F 0 5 6 7 8 1 2 B 4 C 3 A 9 0 F E D 0 F E D C B A 1 9 2 3 4 5 6 7 8 D E F 0 9 A 3 C 4 B 2 1 8 7 6 5 A 9 C B E 5 0 F 7 8 D 6 3 4 1 2 B C 9 A 7 0 D E 6 5 8 F 2 1 4 3 F 0 D 6 B C 9 A 2 1 4 3 E 5 8 7 E D 8 F A 9 C B 3 4 1 2 7 0 5 6 9 2 B C D E F 0 8 7 6 5 4 3 A 1 4 B A 9 0 F E D 5 6 7 8 1 2 3 C превышает максимум 2097152 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Как я уже писала, для порядка 16 существует полная система MOLS, состоящая из 15 ЛК. Её можно построить в матпакете Maple. Было бы интересно её увидеть здесь. Если кто построит, пожалуйста, покажите. В статье http://www.natalimak1.narod.ru/grolk.htm показана ортогональная пара ДЛК 16-го порядка, построенная мной вручную по аналогии с ортогональной парой 8-го порядка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 14 15 12 13 10 11 8 9 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 12 13 14 15 8 9 10 11 4 5 6 7 0 1 2 3 10 11 8 9 14 15 12 13 2 3 0 1 6 7 4 5 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 1 0 3 2 5 4 7 6 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 4 5 6 7 0 1 2 3 12 13 14 15 8 9 10 11 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 2 3 0 1 6 7 4 5 10 11 8 9 14 15 12 13 1 0 3 2 5 4 7 6 9 8 11 10 13 12 15 14 11 10 9 8 15 14 13 12 3 2 1 0 7 6 5 4 3 2 1 0 7 6 5 4 11 10 9 8 15 14 13 12 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 5 4 7 6 1 0 3 2 13 12 15 14 9 8 11 10 13 12 15 14 9 8 11 10 5 4 7 6 1 0 3 2 7 6 5 4 3 2 1 0 15 14 13 12 11 10 9 8 14 15 12 13 10 11 8 9 6 7 4 5 2 3 0 1 Проверка первого ДЛК из этой ортогональной парой утилитой Harry White Tuesday 2020-06-09 20:24:14 ╠юёъютёъюх тЁхь (чшьр)
Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
1 diagonal Latin
1 double axial symmetric
1 center symmetric
1 nfr
1 self-orthogonalОчень симпатичный квадратик: дважды симметричный по Гергели/Брауну (вертикальная и горизонтальная симметрия), ассоциативный и self orthogonal. Поискать программой Белышева ортогональные диагональные соквадраты к этому ДЛК тоже не удалось, программа ругается :) Число диагональных трансверсалей ДЛК16: 0 1 2 3 4 5 6 7 8 9 A B C D E F 2 3 0 1 6 7 4 5 A B 8 9 E F C D 4 5 6 7 0 1 2 3 C D E F 8 9 A B 6 7 4 5 2 3 0 1 E F C D A B 8 9 8 9 A B C D E F 0 1 2 3 4 5 6 7 A B 8 9 E F C D 2 3 0 1 6 7 4 5 C D E F 8 9 A B 4 5 6 7 0 1 2 3 E F C D A B 8 9 6 7 4 5 2 3 0 1 9 8 B A D C F E 1 0 3 2 5 4 7 6 B A 9 8 F E D C 3 2 1 0 7 6 5 4 D C F E 9 8 B A 5 4 7 6 1 0 3 2 F E D C B A 9 8 7 6 5 4 3 2 1 0 1 0 3 2 5 4 7 6 9 8 B A D C F E 3 2 1 0 7 6 5 4 B A 9 8 F E D C 5 4 7 6 1 0 3 2 D C F E 9 8 B A 7 6 5 4 3 2 1 0 F E D C B A 9 8 превышает максимум 2097152 PS. Ортогональная пара здесь слилась - пробелы исчезли. Смотрите её в моей статье, там пробелы есть. Заодно посмотрите там полную систему MOLS 8-го порядка, построенную в матпакете Maple, это мне прислал М. Алексеев (рис. 6). My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
По аналогии с первым ЛК в полной системе MOLS 8-го порядка (смотрите эту систему в статье, указанной в предыдущем посте) я построила первый ЛК в полной системе MOLS 16-го порядка 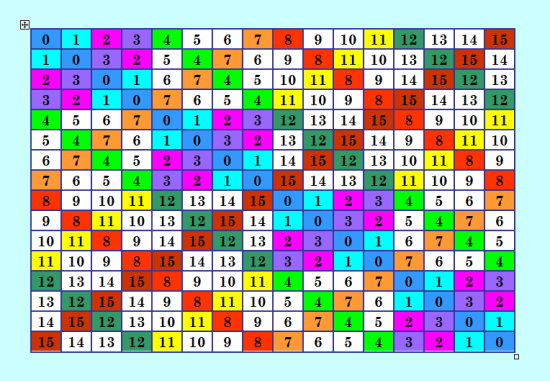 Думаю, что это единственный ЛК, не являющийся ДЛК, как и в системе для порядка 8. Обалденно гармоничный ЛК! На иллюстрации раскраска (частичная) для ассоциативности. Проверка утилитой Harry White выдаёт Wednesday 2020-06-10 08:23:25 ╠юёъютёъюх тЁхь (чшьр)
Order? 16
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
1 Latin
1 double axial symmetric
1 center symmetric
1 nfr
1 nfc
1 nfr nfc
1 self-transposeСколько свойств у этого ЛК! Было очень интересно строить этот ЛК вручную по аналогии с ЛК 8-го порядка. Итак, я уже представила один ЛК и два ДЛК из полной системы MOLS 16-го порядка. Осталось построить ещё 12 ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В статье http://www.natalimak1.narod.ru/dolk.htm, основываясь на методе из статьи Чернова, построена такая ортогональная пара ДЛК 16-го порядка 0 D C B A 11 8 7 5 3 4 2 6 9 10 1 5 1 D C B A 9 8 6 4 3 7 10 11 2 0 4 6 2 D C B 10 9 7 5 8 11 0 3 1 A 9 5 7 3 D C 11 10 8 6 0 1 4 2 A B 1 10 6 8 4 D 0 11 9 7 2 5 3 A B C 3 2 11 7 9 5 1 0 10 8 6 4 A B C D 11 0 1 2 3 4 B A D C 10 9 8 7 6 5 10 11 0 1 2 3 C D A B 9 8 7 6 5 4 8 9 10 11 0 1 A B C D 7 6 5 4 3 2 2 3 4 5 6 7 D C B A 1 0 11 10 9 8 D C B A 10 0 7 6 4 2 11 3 1 5 8 9 C B A 9 11 8 6 5 3 1 D 10 2 0 4 7 B A 8 10 7 6 5 4 2 0 C D 9 1 11 3 A 7 9 6 5 2 4 3 1 11 B C D 8 0 10 6 8 5 4 1 9 3 2 0 10 A B C D 7 11 7 4 3 0 8 10 2 1 11 9 5 A B C D 6 0 11 9 8 10 D 4 6 3 5 A 7 1 B C 2 A 1 0 10 9 11 5 7 4 6 8 2 B C 3 D 9 A 2 1 11 10 6 8 5 7 3 B C 4 D 0 4 10 A 3 2 0 7 9 6 8 B C 5 D 1 11 B 5 11 A 4 3 8 10 7 9 C 6 D 2 0 1 C B 6 0 A 5 9 11 8 10 7 D 3 1 2 4 3 4 5 6 7 8 C D A B 2 1 0 11 10 9 1 2 3 4 5 6 A B C D 0 11 10 9 8 7 2 3 4 5 6 7 B A D C 1 0 11 10 9 8 11 0 1 2 3 4 D C B A 10 9 8 7 6 5 10 8 7 9 D 1 3 5 2 4 11 A 6 0 B C 7 6 8 D 0 C 2 4 1 3 9 10 A 5 11 B 5 7 D 11 C B 1 3 0 2 6 8 9 A 4 10 6 D 10 C B 9 0 2 11 1 4 5 7 8 A 3 D 9 C B 8 2 11 1 10 0 5 3 4 6 7 A 8 C B7 1 A 10 0 9 11 D 4 2 3 5 6 Здесь A, B, C, D – символьные переменные. которые могут принимать значения 12, 13, 14, 15 в разных комбинациях. Первый ДЛК в числах выглядит так (при A=12, B=13, C=14, D=15) 0 15 14 13 12 11 8 7 5 3 4 2 6 9 10 1 5 1 15 14 13 12 9 8 6 4 3 7 10 11 2 0 4 6 2 15 14 13 10 9 7 5 8 11 0 3 1 12 9 5 7 3 15 14 11 10 8 6 0 1 4 2 12 13 1 10 6 8 4 15 0 11 9 7 2 5 3 12 13 14 3 2 11 7 9 5 1 0 10 8 6 4 12 13 14 15 11 0 1 2 3 4 13 12 15 14 10 9 8 7 6 5 10 11 0 1 2 3 14 15 12 13 9 8 7 6 5 4 8 9 10 11 0 1 12 13 14 15 7 6 5 4 3 2 2 3 4 5 6 7 15 14 13 12 1 0 11 10 9 8 15 14 13 12 10 0 7 6 4 2 11 3 1 5 8 9 14 13 12 9 11 8 6 5 3 1 15 10 2 0 4 7 13 12 8 10 7 6 5 4 2 0 14 15 9 1 11 3 12 7 9 6 5 2 4 3 1 11 13 14 15 8 0 10 6 8 5 4 1 9 3 2 0 10 12 13 14 15 7 11 7 4 3 0 8 10 2 1 11 9 5 12 13 14 15 6 Попробовала поискать к этому ДЛК другие ортогональные диагональные соквадраты. В этом случае программа Белышева не ругается, но найти мне ничего не удалось Проверка ДЛК16 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 1879316 Соквадратов: 0 Время в сек: 5055 116138 47232 17897 6268 2036 254 22 19 5 Прервала программу. Второй ДЛК ортогональной пары тоже пыталась проверить Проверка ДЛК16 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 1875976 Соквадратов: 0 Время в сек: 6410 114253 47058 17883 6269 2000 412 120 2 1 Ну и, конечно, прервала, потому что долго нет ни одного соквадрата. Вполне возможно, что они и будут, но дождаться этого здесь нереально. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот, пока всё про ОДЛК 16-го порядка. Перехожу к ОДЛК 17-го порядка. Тут всё очень просто, потому что 17 - простое число. Существует полная система MOLS данного порядка, состоящая из 16 ЛК. Эту систему MOLS можно элементарно построить вручную методом циклического сдвига; я уже построила такие полные системы MOLS для порядков 11 и 13: для порядка 11 система показана выше. Для примера покажу первый ЛК полной системы MOLS 17-го порядка 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 3 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 4 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 5 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 6 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 7 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 8 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 9 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 10 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 11 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 12 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 13 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 14 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 15 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 16 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Что говорит об этом ЛК утилита Harry White? Сейчас посмотрим Sunday 2020-06-14 10:22:34 ╠юёъютёъюх тЁхь (чшьр)
Order? 17
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_2.txt
Counts
------
1 Latin
1 center symmetric
1 nfr
1 nfc
1 nfr nfc
1 self-transposeАссоциативный и диагонально-симметричный. Это ЛК; в полной системе MOLS 17-го порядка есть ещё один ЛК, остальные все ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В статье "Построение ортогональных ДЛК методом L. Zhu" http://www.natalimak1.narod.ru/dolk.htm я использовала результаты, полученные Черновым по этому методу. В статье представлена такая ортогональная пара 17-го порядка 0 16 15 14 12 9 11 6 5 2 4 7 3 13 8 10 1 3 1 16 0 15 13 10 12 6 5 8 4 14 9 11 2 7 6 4 2 16 1 0 14 11 7 9 5 15 10 12 3 8 13 10 7 5 3 16 2 1 15 8 6 0 11 13 4 9 14 12 7 11 8 6 4 16 3 2 9 1 12 14 5 10 15 13 0 2 8 12 9 7 5 16 4 10 13 15 6 11 0 14 1 3 14 3 9 13 10 8 6 16 11 0 7 12 1 15 2 4 5 1 15 4 10 14 11 9 7 12 8 13 2 0 3 5 6 16 12 13 14 15 0 1 2 3 16 11 10 9 8 7 6 5 4 16 14 13 11 8 10 5 0 4 15 1 3 6 2 12 7 9 13 12 10 7 9 4 15 8 3 16 14 0 2 5 1 11 6 11 9 6 8 3 14 7 5 2 12 16 13 15 1 4 0 10 8 5 7 2 13 6 4 9 1 10 11 16 12 14 0 3 15 4 6 1 12 5 3 8 14 0 7 9 10 16 11 13 15 2 5 0 11 4 2 7 13 1 15 3 6 8 9 16 10 12 14 15 10 3 1 6 12 0 13 14 4 2 5 7 8 16 9 11 9 2 0 5 11 15 12 10 13 14 3 1 4 6 7 16 8 0 15 16 12 11 6 5 9 14 4 10 3 7 8 13 1 2 5 1 0 16 13 12 7 6 15 11 4 8 9 14 2 3 10 12 6 2 1 16 14 13 8 0 5 9 10 15 3 4 11 7 6 13 7 3 2 16 15 14 1 10 11 0 4 5 12 8 9 11 7 14 8 4 3 16 0 2 12 1 5 6 13 9 10 15 13 12 8 15 9 5 4 16 3 2 6 7 14 10 11 0 1 3 14 13 9 0 10 6 5 4 7 8 15 11 12 1 2 16 8 4 15 14 10 1 11 7 5 9 0 12 13 2 3 16 6 4 5 6 7 8 9 10 11 16 3 2 1 0 15 14 13 12 14 16 11 10 5 4 8 1 13 15 3 9 2 6 7 12 0 16 10 9 4 3 7 0 15 12 13 14 2 8 1 5 6 11 9 8 3 2 6 15 14 10 11 16 12 13 1 7 0 4 5 7 2 1 5 14 13 9 4 10 8 16 11 12 0 6 15 3 1 0 4 13 12 8 3 2 9 6 7 16 10 11 15 5 14 15 3 12 11 7 2 1 13 8 0 5 6 16 9 10 14 4 2 11 10 6 1 0 12 3 7 14 15 4 5 16 8 9 13 10 9 5 0 15 11 2 12 6 1 13 14 3 4 16 7 8 Утилита Harry White сообщает об этой паре ДЛК Sunday 2020-06-14 10:52:58 ╠юёъютёъюх тЁхь (чшьр)
Order? 17
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_3.txt
Counts
------
2 diagonal Latin
2 center symmetric
1 orthogonal pairОба ДЛК пары ассоциативные. Попыталась проверить первый ДЛК пары программой Белышева ortogon_u, программа ругается Число диагональных трансверсалей ДЛК17: 0 G F E C 9 B 6 5 2 4 7 3 D 8 A 1 3 1 G 0 F D A C 6 5 8 4 E 9 B 2 7 6 4 2 G 1 0 E B 7 9 5 F A C 3 8 D A 7 5 3 G 2 1 F 8 6 0 B D 4 9 E C 7 B 8 6 4 G 3 2 9 1 C E 5 A F D 0 2 8 C 9 7 5 G 4 A D F 6 B 0 E 1 3 E 3 9 D A 8 6 G B 0 7 C 1 F 2 4 5 1 F 4 A E B 9 7 C 8 D 2 0 3 5 6 G C D E F 0 1 2 3 G B A 9 8 7 6 5 4 G E D B 8 A 5 0 4 F 1 3 6 2 C 7 9 D C A 7 9 4 F 8 3 G E 0 2 5 1 B 6 B 9 6 8 3 E 7 5 2 C G D F 1 4 0 A 8 5 7 2 D 6 4 9 1 A B G C E 0 3 F 4 6 1 C 5 3 8 E 0 7 9 A G B D F 2 5 0 B 4 2 7 D 1 F 3 6 8 9 G A C E F A 3 1 6 C 0 D E 4 2 5 7 8 G 9 B 9 2 0 5 B F C A D E 3 1 4 6 7 G 8 превышает максимум 2097152 Наверное, для таких больших порядков программа Белышева не будет работать. Ну, ортогональную пару ДЛК 17-го порядка мы видим. Ещё несколько ортогональных пар ДЛК данного порядка можно получить из полной системы MOLS. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Порядок 18 проблемный. Расскажу про ОДЛК 18-го порядка далее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Начну с ДЛК 18-го порядка, построенного методом Гергели 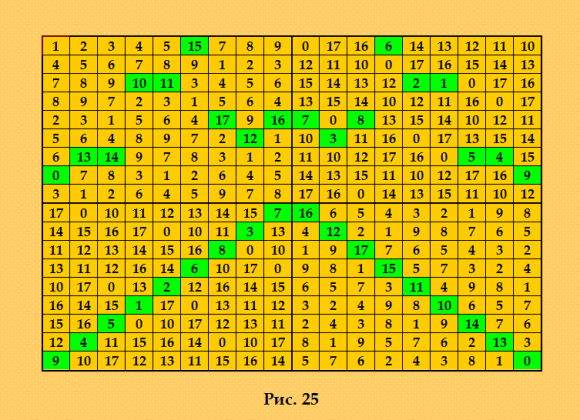 Порядок 18 был для меня сильно проблемным; даже в статье Гергели очень долго не могла с ним разобраться, но, в конце концов, разобралась и ДЛК построила. Утилита Harry White отметила для этого ДЛК только симметричность по Гергели/Брауну Sunday 2020-06-14 21:25:04 ╠юёъютёъюх тЁхь (чшьр)
Order? 18
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail.txt
Counts
------
1 diagonal Latin
1 axial symmetric
Построить ортогональную пару с этим ДЛК не удаётся программой Белышева, опять слишком много диагональных трансверсалей Число диагональных трансверсалей ДЛК18: 1 2 3 4 5 F 7 8 9 0 H G 6 E D C B A 4 5 6 7 8 9 1 2 3 C B A 0 H G F E D 7 8 9 A B 3 4 5 6 F E D C 2 1 0 H G 8 9 7 2 3 1 5 6 4 D F E A C B G 0 H 2 3 1 5 6 4 H 9 G 7 0 8 D F E A C B 5 6 4 8 9 7 2 C 1 A 3 B G 0 H D F E 6 D E 9 7 8 3 1 2 B A C H G 0 5 4 F 0 7 8 3 1 2 6 4 5 E D F B A C H G 9 3 1 2 6 4 5 9 7 8 H G 0 E D F B A C H 0 A B C D E F 7 G 6 5 4 3 2 1 9 8 E F G H 0 A B 3 D 4 C 2 1 9 8 7 6 5 B C D E F G 8 0 A 1 9 H 7 6 5 4 3 2 D B C G E 6 A H 0 9 8 1 F 5 7 3 2 4 A H 0 D 2 C G E F 6 5 7 3 B 4 9 8 1 G E F 1 H 0 D B C 3 2 4 9 8 A 6 5 7 F G 5 0 A H C D B 2 4 3 8 1 9 E 7 6 C 4 B F G E 0 A H 8 1 9 5 7 6 2 D 3 9 A H C D B F G E 5 7 6 2 4 3 8 1 0 превышает максимум 2097152 Ну вот, диагональных трансверсалей очень много, не исключено, что и ортогональные ДЛК имеются. А вот придумайте-ка способ найти хотя бы один ортогональный ДЛК для показанного ДЛК 18-го порядка без программы Белышева, основанной на трансверсальном поиске. Кстати говоря, и трансверсальный поиск можно ведь несколько модифицировать, как мне кажется. Не надо искать все диагональные трансверсали сразу, чтобы они не влезали все в программу; может быть, достаточно какого-то их количества, не превышающего указанный в программе максимум? Задача для Белышева, и не только. Всем, кто серьёзно работает с ОДЛК разных порядков. Ортогональную пару ДЛК 18-го порядка я построила другим методом (не для ДЛК Гергели), расскажу об этом далее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Смотрим мою статью ОРТОГОНАЛЬНЫЕ ДИАГОНАЛЬНЫЕ ЛАТИНСКИЕ КВАДРАТЫ http://www.natalimak1.narod.ru/diagon.htm Сначала о двух статьях, которые я так и не смогла найти в момент написания статьи. Цитирую Назарок А. В. Пары ортогональных дважды диагональных латинских квадратов порядков 15, 18 и 26. // Комбинаторный анализ. Вып. 32. М.: МГУ, 1989 г. Можно и сейчас поискать, вдруг обнаружатся. Далее цитирую Для построения пар ОДЛК 18-го порядка я взяла пару ОЛК из известной группы MOLS данного порядка, состоящей из трёх латинских квадратов. К сожалению, третий латинский квадрат этой группы не превращается в диагональный латинский квадрат. Построение группы MOLS 18-го порядка описано в статье http://www.natalimak1.narod.ru/mols18.htm На рис. 34-35 вы видите ортогональную пару ДЛК 18-го порядка. Сейчас скопирую и покажу здесь. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Встречайте - построенная мной ортогональная пара ДЛК 18-го порядка 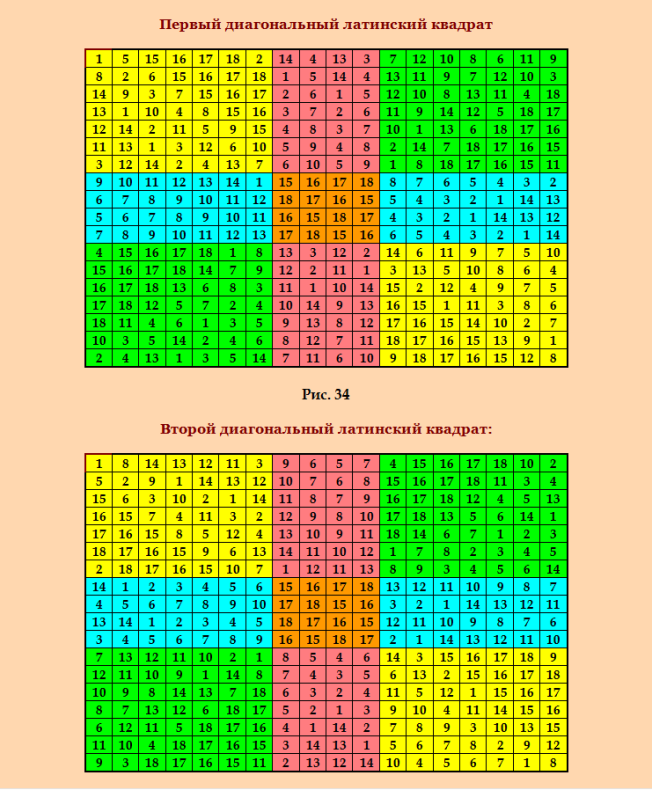 Интересно бы посмотреть на ортогональную пару ДЛК 18-го порядка, построенную в статье Назарок А. В. Пары ортогональных дважды диагональных латинских квадратов порядков 15, 18 и 26. // Комбинаторный анализ. Вып. 32. М.: МГУ, 1989 г. Статья 1989 г., не такая уж и древняя, МГУ; должна бы быть в Сети, но я тогда не нашла. Даже на форуме ПЕН писала об этой статье и просила помочь найти, безуспешно. В статье рассматриваются ортогональные пары ДЛК проблемных порядков 15, 18 и 26. Сейчас преобразую ДЛК из построенной мной ортогональной пары в традиционную форму и проверю их утилитой Harry White. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Преобразовала и проверила ДЛК ортогональной пары 18-го порядка утилитой Harry White Monday 2020-06-15 06:01:31 ╠юёъютёъюх тЁхь (чшьр)
Order? 18
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_1.txt
Counts
------
2 diagonal Latin
1 orthogonal pair
2 self-orthogonalО-о-о! Self orthogonal! Я и не зала о таком понятии в то время, когда писала статью и построила эту ортогональную пару. Каждый ДЛК пары является self orthogonal, то есть мы имеем ещё две ортогональные пары. Поискать новые ортогональные соквадраты к ДЛК этой ортогональной пары, конечно, не удалось Число диагональных трансверсалей ДЛК18: 0 4 E F G H 1 D 3 C 2 6 B 9 7 5 A 8 7 1 5 E F G H 0 4 D 3 C A 8 6 B 9 2 D 8 2 6 E F G 1 5 0 4 B 9 7 C A 3 H C 0 9 3 7 E F 2 6 1 5 A 8 D B 4 H G B D 1 A 4 8 E 3 7 2 6 9 0 C 5 H G F A C 0 2 B 5 9 4 8 3 7 1 D 6 H G F E 2 B D 1 3 C 6 5 9 4 8 0 7 H G F E A 8 9 A B C D 0 E F G H 7 6 5 4 3 2 1 5 6 7 8 9 A B H G F E 4 3 2 1 0 D C 4 5 6 7 8 9 A F E H G 3 2 1 0 D C B 6 7 8 9 A B C G H E F 5 4 3 2 1 0 D 3 E F G H 0 7 C 2 B 1 D 5 A 8 6 4 9 E F G H D 6 8 B 1 A 0 2 C 4 9 7 5 3 F G H C 5 7 2 A 0 9 D E 1 B 3 8 6 4 G H B 4 6 1 3 9 D 8 C F E 0 A 2 7 5 H A 3 5 0 2 4 8 C 7 B G F E D 9 1 6 9 2 4 D 1 3 5 7 B 6 A H G F E C 8 0 1 3 C 0 2 4 D 6 A 5 9 8 H G F E B 7 превышает максимум 2097152 В статье я строила другие подобные ортогональные пары, варьируя квази-разностную матрицу. Но сильно подозреваю сейчас, что все эти пары будут изоморфные, хотя не факт. Надо доказать это или опровергнуть. Программа, написанная в то время (варьирование квази-разностной матрицы), выдала 2880 подобных ортогональных пар. В статье показана 2880-я ортогональная пара. Кажется, это всё у меня по ОДЛК 18-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Поискала две указанные выше статьи. Для Назарок нашла его диссертацию, защищённую, как я поняла, в 1991 г. Исследование ортогональных латинских квадратов и других комбинаторных конструкций Диссертации по физике, математике и химии Статью Назарок А. В. Пары ортогональных дважды диагональных латинских квадратов порядков 15, 18 и 26. // Комбинаторный анализ. Вып. 32. М.: МГУ, 1989 г. не нашла. А вот статью Heinrich K. and Hilton A. J. W. Doubly diagonal orthogonal Latin squares нашла! https://www.sciencedirect.com/science/article/pii/0012365X83902509 Abstract Перевод в Google Пара дважды диагональных ортогональных латинских квадратов порядка n, DDOLS (n), представляет собой пару ортогональных латинских квадратов порядка n со свойством того, что каждый квадрат имеет трансверсаль на передней диагонали (ячейки {(i, i) : 1 <= i <= n}) и обратная диагональ (ячейки {(i, n + 1 − i): 1 <= i <= n}). Покажем, что для всех n, кроме n = 2, 3, 6, 10, 12, 14, 15, 18 и 26, существует пара DDOLS (n). Очевидно, что они не существуют, когда n = 2, 3 и 6. Эта статья 1983 г. Позже были найдены ортогональные пары ДЛК для всех указанных в статье проблемных порядков: 10, 12, 14, 15, 18 и 26. Статью можно посмотреть в PDF. Есть интересные теоремы. Читайте! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот сразу увидела такие две интересные теоремы. Theorem 2.7. Given a pair of DDOLS(a ), and a pair of DDOLS(b), there exists a pair of DDOLS(ab). Эту теорему я хорошо знала уже тогда, когда писала статьи. Применила её для построения ортогональных пар ДЛК 20-го порядка. Дальше покажу эти пары. Theorem 3A (Gergely [5]). There exists a pair of DDOLS(n) for n=p1^e1p2^e2…pk^ek, pi prime, ei a non-negative integer, and pi^ei≥4. Эта теорема, как я понимаю, принадлежит Гергели. По-английски я не чтец. Перевести бы эту статью на русский. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Тэк-с, следующий порядок у нас 19. Хороший порядок :) 19 - простое число. Существует полная система MOLS 19-го порядка, состоящая из 18 взаимно ортогональных ЛК. В этой системе только два ЛК не являются ДЛК. Как я уже сообщала, методом Гергели ДЛК 19-го порядка мне удалось построить только с помощью коллеги Чернова. В статье ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ http://www.natalimak1.narod.ru/dlk.htm этот ДЛК изображён на рис.36. Показываю этот ДЛК 1 18 3 4 5 6 7 8 9 11 0 17 16 15 14 13 12 2 10 2 3 18 5 6 4 8 9 7 10 16 0 17 13 15 14 1 12 11 3 1 2 18 4 5 9 7 8 15 17 16 0 14 13 6 11 10 12 4 5 6 7 18 9 1 2 3 17 12 11 10 0 8 16 15 14 13 5 6 4 8 9 18 2 3 1 16 10 12 11 7 0 17 13 15 14 6 4 5 9 7 8 18 1 2 12 11 10 3 17 16 0 14 13 15 7 8 9 1 2 3 4 18 6 14 15 5 13 12 11 10 0 17 16 8 9 7 2 3 1 5 6 18 13 4 15 14 10 12 11 16 0 17 18 7 8 3 1 2 6 4 5 0 14 13 15 11 10 12 17 16 9 0 11 10 15 17 16 12 14 13 18 8 3 4 2 6 7 5 9 1 17 15 16 11 0 10 14 12 4 3 13 18 5 1 9 2 7 6 8 16 17 15 10 11 0 13 5 12 4 3 14 18 9 2 1 6 8 7 15 16 17 0 10 11 3 13 14 2 5 4 12 18 1 9 8 7 6 14 12 13 17 15 7 11 0 10 6 1 9 2 16 18 8 4 3 5 13 14 12 16 8 15 10 11 0 7 9 2 1 6 17 18 3 5 4 12 13 14 6 16 17 0 10 11 5 2 1 9 8 7 15 18 4 3 11 0 1 14 12 13 17 15 16 9 7 6 8 4 3 5 10 18 2 10 2 0 13 14 12 16 17 15 1 6 8 7 3 5 4 9 11 18 9 10 11 12 13 14 15 16 17 8 18 7 6 5 4 3 2 1 0 Утилита Harry White никаких свойств у этого ДЛК не обнаружила. Имеет ли этот ДЛК ортогональные ДЛК? Программа Белышева ругается :) Число диагональных трансверсалей ДЛК19: 1 I 3 4 5 6 7 8 9 B 0 H G F E D C 2 A 2 3 I 5 6 4 8 9 7 A G 0 H D F E 1 C B 3 1 2 I 4 5 9 7 8 F H G 0 E D 6 B A C 4 5 6 7 I 9 1 2 3 H C B A 0 8 G F E D 5 6 4 8 9 I 2 3 1 G A C B 7 0 H D F E 6 4 5 9 7 8 I 1 2 C B A 3 H G 0 E D F 7 8 9 1 2 3 4 I 6 E F 5 D C B A 0 H G 8 9 7 2 3 1 5 6 I D 4 F E A C B G 0 H I 7 8 3 1 2 6 4 5 0 E D F B A C H G 9 0 B A F H G C E D I 8 3 4 2 6 7 5 9 1 H F G B 0 A E C 4 3 D I 5 1 9 2 7 6 8 G H F A B 0 D 5 C 4 3 E I 9 2 1 6 8 7 F G H 0 A B 3 D E 2 5 4 C I 1 9 8 7 6 E C D H F 7 B 0 A 6 1 9 2 G I 8 4 3 5 D E C G 8 F A B 0 7 9 2 1 6 H I 3 5 4 C D E 6 G H 0 A B 5 2 1 9 8 7 F I 4 3 B 0 1 E C D H F G 9 7 6 8 4 3 5 A I 2 A 2 0 D E C G H F 1 6 8 7 3 5 4 9 B I 9 A B C D E F G H 8 I 7 6 5 4 3 2 1 0 превышает максимум 2097152 Есть несколько других способов построения ДЛК к заданному ДЛК (помимо трансверсального поиска). Например, иногда достаточно исходный ДЛК повернуть на 90 градусов и ортогональный ДЛК готов. Или ещё: иногда ортогональные ДЛК находятся перестановкой строк в заданном ДЛК. Поиграйтесь, господа :) Впрочем, ортогональные пары ДЛК 19-го порядка у нас имеются (из полной системы MOLS). Следующий порядок у нас 20. Расскажу о нём далее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Как всегда, начну с ДЛК 20-го порядка, построенного методом Гергели  Утилита Harry White отметила в этом ДЛК только симметричность по Гергели/Брауну. Есть ли у этого ДЛК ортогональные ДЛК? А чёрт их знает. Программа Белышева ругается Число диагональных трансверсалей ДЛК20: 1 C 3 4 5 6 7 8 9 A 0 J I H G F E D 2 B 9 3 H 5 1 A 6 4 8 2 C I E G 0 B F 7 D J 3 4 5 0 9 2 1 6 7 8 I H G B C J A F E D 4 5 1 9 I 3 2 A 6 7 H G 0 C D 8 J B F E G 1 9 3 4 7 8 2 A 5 F 0 C I H E D J B 6 7 6 A 2 3 8 J 1 5 4 E F B 9 I D C 0 G H 8 7 6 1 2 9 A F 4 3 D E 5 0 J C B G H I 2 8 4 6 A 1 5 7 D 9 J 3 H F B 0 G E I C A 9 8 7 6 5 4 3 2 B 1 C D E F G H I J 0 5 A 2 8 7 E 3 9 1 6 G B J D 4 H I C 0 F 0 J I H G F E D C 1 B 2 3 4 5 6 7 8 9 A C I E G 0 B F H 3 J 9 D 7 5 1 A 6 4 8 2 I H G B C J 0 5 E D 3 4 F A 9 2 1 6 7 8 H G 0 C D I 9 B F E 4 5 1 J 8 3 2 A 6 7 F 0 C I H 4 D J B G 6 1 9 3 E 7 8 2 A 5 E F B J 8 D C 0 G H 7 6 A 2 3 I 9 1 5 4 D E F A J C B G H I 8 7 6 1 2 9 0 5 4 3 J D 7 F B 0 G E I C 2 8 4 6 A 1 5 H 3 9 B 2 D E F G H I J 0 A 9 8 7 6 5 4 3 C 1 6 B J D E H I C 0 F 5 A 2 8 7 4 3 9 1 G превышает максимум 2097152 Неужели при таком огромном количестве диагональных трансверсалей не найдётся ни одного ортогонального диагонального соквадрата? Ну вот, у ДЛК Гергели 20-го порядка ортогональной пары не имеем пока. Может быть, кто-нибудь найдёт в будущем. Например, Белышев модифицирует свою программу трансверсального поиска и найдёт. Однако порядок 20 хорош тем, что 20=4*5, и для порядков 4 и 5 существуют ортогональные пары ДЛК. Вот я и применила к этому порядку показанную выше теорему. Расскажу об этом далее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Метод построения ортогональных пар ЛК, основанный на теореме Theorem 2.7. Given a pair of DDOLS(a ), and a pair of DDOLS(b), there exists a pair of DDOLS(ab). я называю методом составных квадратов. В статье ГРУППЫ MOLS 20-го и 21-го ПОРЯДКА http://www.natalimak1.narod.ru/mols20_21.htm на рис. 12-14 показана группа MOLS 20-го порядка, состоящая из трёх взаимно ортогональных ЛК, построенная методом составных квадратов. Показываю эту группу №1 1 2 3 4 5 6 7 8 9 10 16 17 18 19 20 11 12 13 14 15 3 4 5 1 2 8 9 10 6 7 18 19 20 16 17 13 14 15 11 12 5 1 2 3 4 10 6 7 8 9 20 16 17 18 19 15 11 12 13 14 2 3 4 5 1 7 8 9 10 6 17 18 19 20 16 12 13 14 15 11 4 5 1 2 3 9 10 6 7 8 19 20 16 17 18 14 15 11 12 13 11 12 13 14 15 16 17 18 19 20 6 7 8 9 10 1 2 3 4 5 13 14 15 11 12 18 19 20 16 17 8 9 10 6 7 3 4 5 1 2 15 11 12 13 14 20 16 17 18 19 10 6 7 8 9 5 1 2 3 4 12 13 14 15 11 17 18 19 20 16 7 8 9 10 6 2 3 4 5 1 14 15 11 12 13 19 20 16 17 18 9 10 6 7 8 4 5 1 2 3 6 7 8 9 10 1 2 3 4 5 11 12 13 14 15 16 17 18 19 20 8 9 10 6 7 3 4 5 1 2 13 14 15 11 12 18 19 20 16 17 10 6 7 8 9 5 1 2 3 4 15 11 12 13 14 20 16 17 18 19 7 8 9 10 6 2 3 4 5 1 12 13 14 15 11 17 18 19 20 16 9 10 6 7 8 4 5 1 2 3 14 15 11 12 13 19 20 16 17 18 16 17 18 19 20 11 12 13 14 15 1 2 3 4 5 6 7 8 9 10 18 19 20 16 17 13 14 15 11 12 3 4 5 1 2 8 9 10 6 7 20 16 17 18 19 15 11 12 13 14 5 1 2 3 4 10 6 7 8 9 17 18 19 20 16 12 13 14 15 11 2 3 4 5 1 7 8 9 10 6 19 20 16 17 18 14 15 11 12 13 4 5 1 2 3 9 10 6 7 8 №2 1 2 3 4 5 11 12 13 14 15 6 7 8 9 10 16 17 18 19 20 4 5 1 2 3 14 15 11 12 13 9 10 6 7 8 19 20 16 17 18 2 3 4 5 1 12 13 14 15 11 7 8 9 10 6 17 18 19 20 16 5 1 2 3 4 15 11 12 13 14 10 6 7 8 9 20 16 17 18 19 3 4 5 1 2 13 14 15 11 12 8 9 10 6 7 18 19 20 16 17 6 7 8 9 10 16 17 18 19 20 1 2 3 4 5 11 12 13 14 15 9 10 6 7 8 19 20 16 17 18 4 5 1 2 3 14 15 11 12 13 7 8 9 10 6 17 18 19 20 16 2 3 4 5 1 12 13 14 15 11 10 6 7 8 9 20 16 17 18 19 5 1 2 3 4 15 11 12 13 14 8 9 10 6 7 18 19 20 16 17 3 4 5 1 2 13 14 15 11 12 16 17 18 19 20 6 7 8 9 10 11 12 13 14 15 1 2 3 4 5 19 20 16 17 18 9 10 6 7 8 14 15 11 12 13 4 5 1 2 3 17 18 19 20 16 7 8 9 10 6 12 13 14 15 11 2 3 4 5 1 20 16 17 18 19 10 6 7 8 9 15 11 12 13 14 5 1 2 3 4 18 19 20 16 17 8 9 10 6 7 13 14 15 11 12 3 4 5 1 2 11 12 13 14 15 1 2 3 4 5 16 17 18 19 20 6 7 8 9 10 14 15 11 12 13 4 5 1 2 3 19 20 16 17 18 9 10 6 7 8 12 13 14 15 11 2 3 4 5 1 17 18 19 20 16 7 8 9 10 6 15 11 12 13 14 5 1 2 3 4 20 16 17 18 19 10 6 7 8 9 13 14 15 11 12 3 4 5 1 2 18 19 20 16 17 8 9 10 6 7 №3 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 2 3 4 5 1 7 8 9 10 6 12 13 14 15 11 17 18 19 20 16 3 4 5 1 2 8 9 10 6 7 13 14 15 11 12 18 19 20 16 17 4 5 1 2 3 9 10 6 7 8 14 15 11 12 13 19 20 16 17 18 5 1 2 3 4 10 6 7 8 9 15 11 12 13 14 20 16 17 18 19 6 7 8 9 10 1 2 3 4 5 16 17 18 19 20 11 12 13 14 15 7 8 9 10 6 2 3 4 5 1 17 18 19 20 16 12 13 14 15 11 8 9 10 6 7 3 4 5 1 2 18 19 20 16 17 13 14 15 11 12 9 10 6 7 8 4 5 1 2 3 19 20 16 17 18 14 15 11 12 13 10 6 7 8 9 5 1 2 3 4 20 16 17 18 19 15 11 12 13 14 11 12 13 14 15 16 17 18 19 20 1 2 3 4 5 6 7 8 9 10 12 13 14 15 11 17 18 19 20 16 2 3 4 5 1 7 8 9 10 6 13 14 15 11 12 18 19 20 16 17 3 4 5 1 2 8 9 10 6 7 14 15 11 12 13 19 20 16 17 18 4 5 1 2 3 9 10 6 7 8 15 11 12 13 14 20 16 17 18 19 5 1 2 3 4 10 6 7 8 9 16 17 18 19 20 11 12 13 14 15 6 7 8 9 10 1 2 3 4 5 17 18 19 20 16 12 13 14 15 11 7 8 9 10 6 2 3 4 5 1 18 19 20 16 17 13 14 15 11 12 8 9 10 6 7 3 4 5 1 2 19 20 16 17 18 14 15 11 12 13 9 10 6 7 8 4 5 1 2 3 20 16 17 18 19 15 11 12 13 14 10 6 7 8 9 5 1 2 3 4 Понятно, что эта группа MOLS построена на основе групп MOLS 4-го и 5-го порядков. ЛК №1 и №2 в этой группе MOLS 20-го порядка являются диагональными. Имеем одну ортогональную пару ДЛК 20-го порядка. Сейчас преобразую ДЛК этой ортогональной пары в традиционную форму и проверю утилитой Harry White. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила утилитой Harry White все три ЛК показанной группы MOLS 20-го порядка Monday 2020-06-15 19:20:25 ╠юёъютёъюх тЁхь (чшьр)
Order? 20
Enter the name of the squares file: INP
.. writing type information to file INPTypeDetail_2.txt
Counts
------
1 Latin
2 diagonal Latin
3 center symmetric
1 nfr
1 nfc
1 nfr nfc
1 self-transpose
2 orthogonal pair
2 self-orthogonalИнтересные свойства! Все три квадрата ассоциативные. Один квадрат диагонально-симметричный. Два квадрата self orthogonal. Диагонально-симметричным является ЛК №3 (не диагональный). Я не понимаю, как Harry считает ортогональные пары. Почему в этой системе MOLS у него всего две ортогональные пары??? Ведь здесь же три ортогональные пары, потому что квадраты взаимно ортогональны. PS. А, кажется понимаю. У Harry третья ортогональная пара входит в пункт 2 self-orthogonal Да, оба ДЛК в этой системе MOLS являются self orthogonal, и дают они как раз одну ортогональную пару. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
В статье ЕЩЁ ОДНА ГРУППА MOLS 20-го ПОРЯДКА http://www.natalimak1.narod.ru/mols20a.htm построена ещё одна группа MOLS 20-го порядка, состоящая из четырёх взаимно ортогональных ЛК. При построении использовалась квази-разностная матрица, приведённая в статье M. Wojtas, Discrete Mathematics 140 (1995) 291 - 294 Один ЛК в этой группе MOLS является диагональным, первый. Показываю его  Интереснейший ДЛК! Своеобразная блочная структура. И блоки весьма своеобразные. Сейчас проверю этот ДЛК утилитой Harry White. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот Tuesday 2020-06-16 07:34:17 ╠юёъютёъюх тЁхь (чшьр)
Order? 20
Enter the name of the squares file: inp
.. writing type information to file inpTypeDetail_4.txt
Counts
------
1 diagonal Latin
1 natural \diagonal
1 self-orthogonalО-о-о! Self orthogonal! Таким образом, имеем ещё одну очень оригинальную ортогональную пару ДЛК 20-го порядка: показанный на иллюстрации в предыдущем посте ДЛК ортогонален своему транспонированному варианту. Прекрасная ортогональная пара! Вполне возможно, что у этого ДЛК есть и другие ортогональные диагональные соквадраты, но найти их проблематично. Программа Белышева наверняка будет ругаться :) Да, ругается Число диагональных трансверсалей ДЛК20: 0 B 9 I H 6 5 E 3 C 1 A 8 J G 7 4 F 2 D A 1 J 8 7 G F 4 D 2 B 0 I 9 6 H E 5 C 3 4 F 2 D B 0 J 8 7 G 5 E 3 C A 1 I 9 6 H E 5 C 3 1 A 9 I H 6 F 4 D 2 0 B 8 J G 7 8 J 6 H 4 F D 2 1 A 9 I 7 G 5 E C 3 0 B I 9 G 7 E 5 3 C B 0 J 8 H 6 F 4 2 D A 1 2 D A 1 8 J 6 H F 4 3 C B 0 9 I 7 G E 5 C 3 0 B I 9 G 7 5 E D 2 1 A J 8 H 6 4 F G 7 4 F C 3 A 1 8 J H 6 5 E D 2 B 0 9 I 6 H E 5 2 D 0 B I 9 7 G F 4 3 C 1 A J 8 B 0 I 9 6 H E 5 C 3 A 1 J 8 7 G F 4 D 2 1 A 8 J G 7 4 F 2 D 0 B 9 I H 6 5 E 3 C F 4 D 2 0 B 8 J G 7 E 5 C 3 1 A 9 I H 6 5 E 3 C A 1 I 9 6 H 4 F 2 D B 0 J 8 7 G J 8 H 6 F 4 2 D A 1 I 9 G 7 E 5 3 C B 0 9 I 7 G 5 E C 3 0 B 8 J 6 H 4 F D 2 1 A D 2 1 A J 8 H 6 4 F C 3 0 B I 9 G 7 5 E 3 C B 0 9 I 7 G E 5 2 D A 1 8 J 6 H F 4 7 G F 4 3 C 1 A J 8 6 H E 5 2 D 0 B I 9 H 6 5 E D 2 B 0 9 I G 7 4 F C 3 A 1 8 J превышает максимум 2097152 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger