ОДЛК для порядков n>10
Message boards :
Science :
ОДЛК для порядков n>10
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Продолжаю тему, начатую тут https://boinc.progger.info/odlk/forum_thread.php?id=158&postid=5679#5679 Почитав свои статьи одиннадцатилетней давности об ОДЛК порядков n>10, я обнаружила, что у меня есть совсем неплохой задел. Весьма интересно посмотреть на всё это с высоты новых знаний и навыков, приобретённый за последние 4 года в процессе работы с ОДЛК 10-го порядка. Расскажу о ДЛК 12-го порядка. Очень долго я не могла найти не только пару ортогональных ДЛК данного порядка, но и построить один ДЛК. Наконец, повезло со статьёй Ervin Gergely. A Simple Method for Constructing Doubly Diagonalized Latin Squares. 1972 (статья выложена на Яндекс.Диск https://yadi.sk/i/reXszmOC3RFUQC ) Кстати, статья Гергели была написана в 1972 г., а симметрия, которую мы обнаружили в ДЛК Брауна и компании (1992 г.), в ДЛК Гергели уже была. И "брауны" тоже были. Вот почему я назвала эту симметрию симметрией Гергели/Брауна. В статье Гергели я нашла описание способов построения ДЛК всех серий порядков. Разбиралась с этими способами очень долго, некоторые серии порядков сразу поддались, а с некоторыми пришлось повозиться. А, например, для порядка 19 могла построить ДЛК методом Гергели только с помощью коллеги Чернова. Хотя это не проблемный порядок, для него можно элементарно вручную построить ДЛК. Мою статью о построении ДЛК методом Гергели ПОСТРОЕНИЕ ДИАГОНАЛЬНЫХ ЛАТИНСКИХ КВАДРАТОВ смотрите тут http://www.natalimak1.narod.ru/dlk.htm ДЛК 12-го порядка мне удалось построить методом Гергели  Далее покажу немного раскрашенную вертикальную симметрию в этом ДЛК, она очень красивая. "Браунизм" виден и на показанной иллюстрации. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, ещё раз ДЛК 12-го порядка, построенный методом Гергели 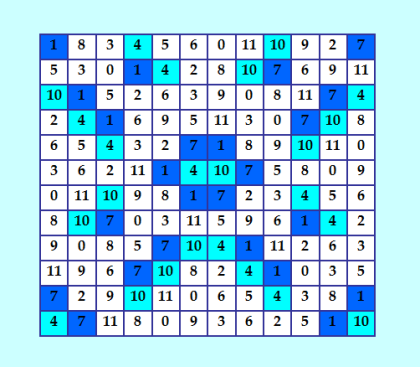 Вот такой красивый ДЛК. А дальше естественно возникает вопрос: есть ли у этого красивого ДЛК ортогональные ДЛК? В то время для меня было трудно найти ответ на этот вопрос. Сейчас у нас есть замечательная программа Белышева ortogon_u, которая может помочь найти ответ. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А теперь о ДЛК и ОДЛК порядка 11. Ну, это легко, потому что порядок 11 - простое число. Существует полная система из 10 взаимно ортогональных ЛК данного порядка (из них только два не ДЛК). Эту систему можно построить в пакете Maple. Пакета Maple у меня нет. В то время, когда я писала статьи о ЛК, мне некоторые полные системы, построенные в пакете Maple, прислал коллега М. Алексеев; некоторые прислал друг. В моей статье "Построение диагональных латинских квадратов" ДЛК 11-го порядка, построенный методом Гергели, показан на рис. 7. Не буду дублировать его здесь. Этот ДЛК был приведён в статье Гергели в качестве примера, так что мне его не пришлось строить. А сейчас я просто построила все 10 ЛК полной системы взаимно ортогональных ЛК 11-го порядка вручную. Это делается элементарно методом циклического сдвига. Смотрите эти ЛК далее. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Встречайте: полная система взаимно ортогональных ЛК 11-го порядка, построенная вручную методом циклического сдвига №1 0 1 2 3 4 5 6 7 8 9 10 1 2 3 4 5 6 7 8 9 10 0 2 3 4 5 6 7 8 9 10 0 1 3 4 5 6 7 8 9 10 0 1 2 4 5 6 7 8 9 10 0 1 2 3 5 6 7 8 9 10 0 1 2 3 4 6 7 8 9 10 0 1 2 3 4 5 7 8 9 10 0 1 2 3 4 5 6 8 9 10 0 1 2 3 4 5 6 7 9 10 0 1 2 3 4 5 6 7 8 10 0 1 2 3 4 5 6 7 8 9 №2 0 1 2 3 4 5 6 7 8 9 10 2 3 4 5 6 7 8 9 10 0 1 4 5 6 7 8 9 10 0 1 2 3 6 7 8 9 10 0 1 2 3 4 5 8 9 10 0 1 2 3 4 5 6 7 10 0 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 8 9 10 0 3 4 5 6 7 8 9 10 0 1 2 5 6 7 8 9 10 0 1 2 3 4 7 8 9 10 0 1 2 3 4 5 6 9 10 0 1 2 3 4 5 6 7 8 №3 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 0 1 2 6 7 8 9 10 0 1 2 3 4 5 9 10 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 0 4 5 6 7 8 9 10 0 1 2 3 7 8 9 10 0 1 2 3 4 5 6 10 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 0 1 5 6 7 8 9 10 0 1 2 3 4 8 9 10 0 1 2 3 4 5 6 7 №4 0 1 2 3 4 5 6 7 8 9 10 4 5 6 7 8 9 10 0 1 2 3 8 9 10 0 1 2 3 4 5 6 7 1 2 3 4 5 6 7 8 9 10 0 5 6 7 8 9 10 0 1 2 3 4 9 10 0 1 2 3 4 5 6 7 8 2 3 4 5 6 7 8 9 10 0 1 6 7 8 9 10 0 1 2 3 4 5 10 0 1 2 3 4 5 6 7 8 9 3 4 5 6 7 8 9 10 0 1 2 7 8 9 10 0 1 2 3 4 5 6 №5 0 1 2 3 4 5 6 7 8 9 10 5 6 7 8 9 10 0 1 2 3 4 10 0 1 2 3 4 5 6 7 8 9 4 5 6 7 8 9 10 0 1 2 3 9 10 0 1 2 3 4 5 6 7 8 3 4 5 6 7 8 9 10 0 1 2 8 9 10 0 1 2 3 4 5 6 7 2 3 4 5 6 7 8 9 10 0 1 7 8 9 10 0 1 2 3 4 5 6 1 2 3 4 5 6 7 8 9 10 0 6 7 8 9 10 0 1 2 3 4 5 №6 0 1 2 3 4 5 6 7 8 9 10 6 7 8 9 10 0 1 2 3 4 5 1 2 3 4 5 6 7 8 9 10 0 7 8 9 10 0 1 2 3 4 5 6 2 3 4 5 6 7 8 9 10 0 1 8 9 10 0 1 2 3 4 5 6 7 3 4 5 6 7 8 9 10 0 1 2 9 10 0 1 2 3 4 5 6 7 8 4 5 6 7 8 9 10 0 1 2 3 10 0 1 2 3 4 5 6 7 8 9 5 6 7 8 9 10 0 1 2 3 4 №7 0 1 2 3 4 5 6 7 8 9 10 7 8 9 10 0 1 2 3 4 5 6 3 4 5 6 7 8 9 10 0 1 2 10 0 1 2 3 4 5 6 7 8 9 6 7 8 9 10 0 1 2 3 4 5 2 3 4 5 6 7 8 9 10 0 1 9 10 0 1 2 3 4 5 6 7 8 5 6 7 8 9 10 0 1 2 3 4 1 2 3 4 5 6 7 8 9 10 0 8 9 10 0 1 2 3 4 5 6 7 4 5 6 7 8 9 10 0 1 2 3 №8 0 1 2 3 4 5 6 7 8 9 10 8 9 10 0 1 2 3 4 5 6 7 5 6 7 8 9 10 0 1 2 3 4 2 3 4 5 6 7 8 9 10 0 1 10 0 1 2 3 4 5 6 7 8 9 7 8 9 10 0 1 2 3 4 5 6 4 5 6 7 8 9 10 0 1 2 3 1 2 3 4 5 6 7 8 9 10 0 9 10 0 1 2 3 4 5 6 7 8 6 7 8 9 10 0 1 2 3 4 5 3 4 5 6 7 8 9 10 0 1 2 №9 0 1 2 3 4 5 6 7 8 9 10 9 10 0 1 2 3 4 5 6 7 8 7 8 9 10 0 1 2 3 4 5 6 5 6 7 8 9 10 0 1 2 3 4 3 4 5 6 7 8 9 10 0 1 2 1 2 3 4 5 6 7 8 9 10 0 10 0 1 2 3 4 5 6 7 8 9 8 9 10 0 1 2 3 4 5 6 7 6 7 8 9 10 0 1 2 3 4 5 4 5 6 7 8 9 10 0 1 2 3 2 3 4 5 6 7 8 9 10 0 1 №10 0 1 2 3 4 5 6 7 8 9 10 10 0 1 2 3 4 5 6 7 8 9 9 10 0 1 2 3 4 5 6 7 8 8 9 10 0 1 2 3 4 5 6 7 7 8 9 10 0 1 2 3 4 5 6 6 7 8 9 10 0 1 2 3 4 5 5 6 7 8 9 10 0 1 2 3 4 4 5 6 7 8 9 10 0 1 2 3 3 4 5 6 7 8 9 10 0 1 2 2 3 4 5 6 7 8 9 10 0 1 1 2 3 4 5 6 7 8 9 10 0 У кого есть пакет Maple, проверьте. Как видим, в полной системе только два ЛК не являются ДЛК: №1 и №10. Подчёркиваю: это взаимно ортогональные ДЛК. Так что, здесь уже имеется куча ортогональных пар ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Для исследования на ОДЛК взяла квадрат №2 из показанной полной системы  Красавец! Ассоциативный, пандиагональный (то есть ultra) и self orthogonal. Раскраской показана ассоциативность. Как вы думаете, много ли ортогональных диагональных соквадратов имеет этот красавец? My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Протокол работы программы Белышева ortogon_u Проверка ДЛК11 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 4523 Соквадратов: 19139 Время в сек: 4250 1 86 2 5 5 2 Для выхода нажмите любую клавишу: Итак, показанный красавец 11-го порядка имеет 19139 ортогональных диагональных соквадратов. Круто! My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Смотрим последовательность в OEIS https://oeis.org/A287695 A287695 Maximum number of normalized diagonal Latin squares that can be orthogonal to the same diagonal Latin square of order n. 1, 0, 0, 1, 1, 0, 3, 824 Цитата a(9) >= 516. - Eduard I. Vatutin, Oct 18 2017 Собственно, результат a(10) >= 10 найден мной, там указана ссылка N. Makarova, Diagonal Latin square with 10 orthogonal squares Теперь уже можно добавить результат a(11) >= 19139 Пока я хочу проверить остальные семь ДЛК из полной системы 11-го порядка. Может быть, какой-то из них имеет больше ортогональных ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У меня досчитывается сейчас проверка на ОДЛК ДЛК 12-го порядка. Черепашка мужественно выдержала ночную работу, потому что прерывать программу нельзя. Программа работала больше суток. Вот-вот закончится. Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 8760 Соквадратов: 40983 Время в сек: 105710 5 17 71 32 1 1 О ДЛК, который здесь проверяется, расскажу позже. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
У-р-р-р-а!!! - кричим мы вместе с черепашкой :) Досчиталось! Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 8760 Соквадратов: 41644 Время в сек: 106380 1 4 19 4 4 9 3 Для выхода нажмите любую клавишу: Найдено 41644 соквадратов! И уже можно добавить в последовательность OEIS результат a(12) >= 41644 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ДЛК 11-го порядка Гергели проверила, он не имеет ни одного ортогонального ДЛК, как, впрочем, и ДЛК 10-го порядка Гергели, который я проверила очень давно. Запустила проверку ДЛК 11-го порядка №3 из полной системы. Интересно, сколько у него ортогональных ДЛК. Ну, для 11-го порядка программа побыстрее работает. Для порядка 12 уже тяжко, а дальше ещё тяжелее. Программа работает Проверка ДЛК11 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 4665 Соквадратов: 6041 Время в сек: 810 290 150 56 4 1 Уже найдено 6041 соквадратов. Кстати, у это ДЛК чуть-чуть побольше диагональных трансверсалей, нежели у ДЛК №2. Поэтому вполне может быть и ортогональных соквадратов больше. Ждём-с. О ДЛК 12-го порядка начну рассказывать после проверки всех ДЛК 11-го порядка из полной системы. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
ДЛК №3 отстрелялся Проверка ДЛК11 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 4665 Соквадратов: 26914 Время в сек: 3535 1 83 24 8 4 1 Для выхода нажмите любую клавишу: Как и ожидалось, этот ДЛК имеет больше ортогональных соквадратов, чем ДЛК №2. Ну, проверю остальные шесть ДЛК, сообщу сразу все результаты. А пока a(11)>=26914. Да, проверка утилитой Harry White ДЛК №3 Sunday 2020-06-07 14:18:01 ╠юёъютёъюх тЁхь (чшьр)
Order? 11
Enter the name of the squares file: input
.. writing type information to file inputTypeDetail_9.txt
Counts
------
1 diagonal Latin
1 pandiagonal
1 center symmetric
1 nfr
1 self-orthogonal
Как и ДЛК №2, он ассоциативный, пандиагональный и self orthogonal. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила все ДЛК 11-го порядка из полной системы. ДЛК №№ 3,4,7,8 имеют 26914 ортогональных дигональных соквадратов; остальные ДЛК имеют 19139 ортогональных диагональных соквадратов. Выклдывать буду 26914 ортогональных ДЛК для ДЛК №3 0 1 2 3 4 5 6 7 8 9 10 3 4 5 6 7 8 9 10 0 1 2 6 7 8 9 10 0 1 2 3 4 5 9 10 0 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 9 10 0 4 5 6 7 8 9 10 0 1 2 3 7 8 9 10 0 1 2 3 4 5 6 10 0 1 2 3 4 5 6 7 8 9 2 3 4 5 6 7 8 9 10 0 1 5 6 7 8 9 10 0 1 2 3 4 8 9 10 0 1 2 3 4 5 6 7 Покажу первые 5 ортогональных диагональных соквадратов (я все соквадраты нормализовала) 0 1 2 3 4 5 6 7 8 9 10 9 8 3 10 1 6 0 4 2 7 5 1 3 9 7 2 8 5 0 6 10 4 10 6 4 2 3 0 1 8 9 5 7 8 9 10 6 7 4 2 5 3 0 1 5 0 7 9 10 1 3 6 4 8 2 4 2 5 8 9 3 10 1 7 6 0 7 10 6 4 5 2 9 3 0 1 8 6 7 0 1 8 10 4 2 5 3 9 2 5 8 0 6 9 7 10 1 4 3 3 4 1 5 0 7 8 9 10 2 6 0 1 2 3 4 5 6 7 8 9 10 9 8 6 10 1 3 5 4 2 7 0 1 0 10 2 6 7 9 8 5 3 4 8 7 5 4 10 0 1 9 3 2 6 6 3 7 9 2 4 8 0 10 5 1 7 10 8 5 9 1 3 6 0 4 2 10 5 4 0 3 2 7 1 6 8 9 2 9 3 6 8 10 0 5 4 1 7 5 4 0 1 7 6 2 3 9 10 8 3 2 9 7 0 8 4 10 1 6 5 4 6 1 8 5 9 10 2 7 0 3 0 1 2 3 4 5 6 7 8 9 10 4 10 0 7 1 6 3 9 2 5 8 1 6 5 8 2 9 4 10 0 3 7 5 8 7 6 0 2 1 3 4 10 9 3 5 6 0 9 8 2 4 10 7 1 2 4 10 9 3 1 0 8 7 6 5 8 0 4 5 6 10 7 1 9 2 3 6 3 9 4 10 7 8 2 5 1 0 9 7 8 1 5 0 10 6 3 4 2 10 9 3 2 7 4 5 0 1 8 6 7 2 1 10 8 3 9 5 6 0 4 0 1 2 3 4 5 6 7 8 9 10 6 8 0 4 1 10 7 9 2 3 5 1 3 6 8 0 4 9 10 5 2 7 10 6 3 5 7 2 1 8 9 4 0 8 4 9 0 10 7 2 3 6 5 1 3 9 5 10 2 1 8 6 7 0 4 5 7 4 2 9 0 3 1 10 6 8 7 5 10 6 8 9 4 2 0 1 3 9 10 7 1 3 6 5 0 4 8 2 2 0 8 9 5 3 10 4 1 7 6 4 2 1 7 6 8 0 5 3 10 9 0 1 2 3 4 5 6 7 8 9 10 7 6 4 10 1 9 0 3 2 5 8 1 10 3 6 9 8 2 5 4 7 0 5 2 10 4 3 6 1 9 0 8 7 9 4 5 2 8 7 3 6 10 0 1 8 7 9 0 10 1 5 4 3 6 2 4 0 7 8 6 10 9 1 5 2 3 6 5 8 7 0 3 10 2 9 1 4 10 9 0 1 5 2 4 8 7 3 6 3 8 6 5 2 4 7 0 1 10 9 2 3 1 9 7 0 8 10 6 4 5 Ортогональность проверила своей программой проверки ортогональности. Все 26914 ДЛК ортогональны исходному ДЛК. Выложила ортогональные соквадраты к ДЛК №3 на Яндекс.Диск https://yadi.sk/d/TftPoOYfeF5QcQ My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Возможно, существует такой ДЛК 11-го порядка, который имеет больше 26914 ортогональных ДЛК, но я не знаю, как его можно найти. Поэтому пока удовлетворюсь найденным результатом для ОДЛК 11-го порядка и перехожу к ОДЛК 12-го порядка. Здесь, как я уже писала, результат тоже уже получен, это результат для ДЛК, построенного А. Черновым. Но сначала расскажу о ДЛК 12-го порядка, построенном методом Гергели. Рассказ о нём уже был начат выше. Цитата Итак, ещё раз ДЛК 12-го порядка, построенный методом Гергели Да, программа Белышева помогла найти ответ. Показанный ДЛК 12-го порядка имеет 2199 ортогональных диагональных соквадратов. Протокол работы программы Белышева Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 5718 Соквадратов: 2199 Время в сек: 1155 1 28 13 4 2 2 Для выхода нажмите любую клавишу: Тут у меня возникает вопрос: а есть ли среди всех этих ортогональных диагональных соквадратов MODLS из 3 и/или более ОДЛК? Надо это проверить. Весьма любопытно! Далее расскажу о ДЛК 12-го порядка Чернова. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А. Чернов построил ортогональную пару ДЛК 12-го порядка в статье "ОДЛК. Метод Пелегрино-Ланселотти" http://alex-black.ru/article.php?content=124 Он ссылается на следующую статью Consolato Pellegrino and Paola Lancellotti. A New Construction of Doubly Diagonal Orthogonal Latin Squares Оригинальный ДЛК этой ортогональной пары (первый) вы можете увидеть в указанной статье Чернова. Я покажу этот ДЛК в другой раскраске 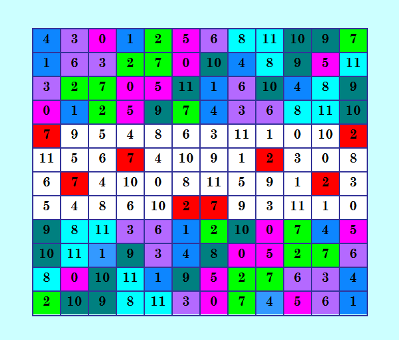 Очень интересный ДЛК! В нём содержатся два вида симметрии: центральная и вертикальная по Гергели/Брауну. На иллюстрации это и показано: верхние 4 строки и нижние 4 строки - центральная симметрия, в средних 4-х строках вертикальная симметрия. Проверила этот ДЛК на ОДЛК программой Белышева. Программа работала больше суток. Протокол работы программы Проверка ДЛК12 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 8760 Соквадратов: 41644 Время в сек: 106380 1 4 19 4 4 9 3 Для выхода нажмите любую клавишу: Найдено 41644 ортогональных диагональных соквадратов! Супер! Конечно, тут большую роль сыграла ассоциативность ДЛК, хотя и частичная. Думаю, что было бы ещё больше ортогональных ДЛК, если бы исходный ДЛК был полностью ассоциативным. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
И здесь, конечно, тот же вопрос: есть ли среди огромного количества ортогональных диагональных соквадратов группы MODLS? Я не помню, чтобы в моих давних статьях такие группы MODLS были найдены для ДЛК 12-го порядка. Может быть, и забыла (всё-таки 11 лет - это достаточно, чтобы забыть). Но помню, что порядок 12 был сильно проблемным. Читайте мои статьи. Если найдёте группы MODLS 12-го порядка, расскажите, пожалуйста :) Пока же мы имеем только ортогональные пары ДЛК 12-го порядка. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Внимание! ГОЛОВОЛОМКА! Ой, вот же как интересно! Чернов в своей статье дал ссылку на мою статью, в которой я строила ортогональные пары с помощью его Приложения (Приложение можно скачать в статье Чернова) http://www.natalimak1.narod.ru/ddolk.htm Открываю свою статью по ссылке Алексея и вижу... сплошные абракадабры :) Это произошло при передаче сайта с narod.ru на Ucoz.ru Многие странички я тогда перекодировала, но вот эта осталась с абракадабрами. 0 2 1 3 3 1 2 0 2 0 3 1 1 3 0 2 0 3 2 1 2 1 0 3 1 2 3 0 3 0 1 2 ¦юыєўшырё№ ярЁр +-T¦ 12-ую яюЁ фър: 4а 3а 0а 2а 1а 6а 5а 8 11а 9 10а 7 а2а 5а 3а 1а 7а 0а 9а 4а 8 10а 6 11 а3а 1а 7а 0а 6 11а 2а 5а 9а 4а 8 10 а0а 2а 1а 6 10а 7а 4а 3а 5а 8 11а 9 а7 10а 6а 4а 8а 5а 3 11а 2а 0а 9а 1 11а 6а 5а 7а 4а 9 10а 2а 1а 3а 0а 8 а5а 7а 4а 9а 0а 8 11а 6 10а 2а 1а 3 а6а 4а 8а 5а 9а 1а 7 10а 3 11а 2а 0 10а 8 11а 3а 5а 2а 1а 9а 0а 7а 4а 6 а9 11а 2 10а 3а 4а 8а 0а 6а 1а 7а 5 а8а 0а 9 11а 2 10а 6а 1а 7а 5а 3а 4 а1а 9 10а 8 11а 3а 0а 7а 4а 6а 5а 2 ---- а8а 1а 0а 3а 2 11 10а 6а 7а 4а 5а 9 а0а 9а 2а 1 10а 3а 7 11а 5а 6а 8а 4 а3а 0 11а 2а 9а 5а 1а 8а 6 10а 4а 7 а1а 2а 3 10а 4а 8а 9а 0 11а 7а 6а 5 а5а 3а 7а 4а 0а 6а 8а 1 10а 9а 2 11 а2а 4а 5а 6а 7а 1а 0а 9а 8 11 10а 3 а4а 7 а6а 0 11а 2а 3а 5а 1а 8а 9 10 а6а 5а 1а 7а 3 10а 4а 2а 9а 0 11а 8 11а 8а 9а 5а 1а 7а 6 10а 4а 2а 3а 0 а9 10а 4а 8а 6а 0 11а 7а 3а 5а 1а 2 10а 6а 8 11а 5а 9а 2а 4а 0а 3а 7а 1 а7 11 10а 9а 8а 4а 5а 3а 2а 1а 0а 6 Судя по всему, здесь приведена ортогональная пара ДЛК 12-го порядка. Но как расшифровать эти квадраты??? Совершенно не помню, что такое а, и как это всё вообще прочитать. Вот вам ГОЛОВОЛОМКА :) Расшифруйте эти ДЛК в ортогональной паре. А вот это ¦юыєўшырё№ ярЁр +-T¦ 12-ую яюЁ фър: чего это написано? :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А это, похоже, магический квадрат, построенный из ортогональной пары ДЛК 12-го порядка :) 57а 38а 1а 28а 15а 84а 71а 103а 140а 113а 126а 94 а25а 70а 39а 14а 95а 4а 116а 60а 102а 127а 81а 137 а40а 13а 96а 3а 82а 138а 26а 69а 115а 59а 101а 128 а2а 27а 16а 83а 125а 93а 58а 37 а72а 104а 139а 114 а90а 124а 80а 53а 97а 67а 45а 134а 35а 10а 111а 24 а135а 77а 66а 91а 56а 110а 121а 34а 21а 48а 11а 100 а65а 92а 55а 109а 12а 99а 136а 78а 122а 33а 22а 47 а79а 54а 98а 68а 112а 23а 89а 123а 46а 133а 36а 9 а132а 105а 142а 42а 62а 32а 19а 119а 5а 87а 52а 73 а118а 143а 29а 129а 43а 49а 108а 8а 76а 18а 86а 63 а107а 7а 117а 144а 30а 130а 75а 17а 85а 64а 44а 50 а20а 120а 131а 106а 141а 41а 6а 88а 51а 74а 61а 31 Если положить a=1... Но как понимать записи: а25а, а40а и т. п.? Вот и такое бывает: что написала - и сама не знаю :) My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ой, пойду заниматься ОДЛК 13-го порядка :) Для ДЛК 13-го порядка, построенного методом Гергели, черепашка уже ищет ортогональные диагональные соквадраты. Пока нашла всего один соквадрат Проверка ДЛК13 на марьяжность (ОДЛК) Введено ДЛК: 1 Найдено ОДЛК: 0 Д-трансверсалей: 12034 Соквадратов: 1 Время в сек: 17740 684 176 33 24 5 2 Что-то не густо. Ещё немного покручу и прерву. Порядок 13 не проблемный, потому что 13 - простое число. Полную систему из 12 взаимно ортогональных ЛК уже составила методом циклического сдвига. Только два ЛК не являются в этой системе ДЛК. Самый первый ЛК обалденно красивый 0 1 2 3 4 5 6 7 8 9 10 11 12 1 2 3 4 5 6 7 8 9 10 11 12 0 2 3 4 5 6 7 8 9 10 11 12 0 1 3 4 5 6 7 8 9 10 11 12 0 1 2 4 5 6 7 8 9 10 11 12 0 1 2 3 5 6 7 8 9 10 11 12 0 1 2 3 4 6 7 8 9 10 11 12 0 1 2 3 4 5 7 8 9 10 11 12 0 1 2 3 4 5 6 8 9 10 11 12 0 1 2 3 4 5 6 7 9 10 11 12 0 1 2 3 4 5 6 7 8 10 11 12 0 1 2 3 4 5 6 7 8 9 11 12 0 1 2 3 4 5 6 7 8 9 10 12 0 1 2 3 4 5 6 7 8 9 10 11 Свойства этого ЛК, выданные утилитой Harry: Latin, center symmetric, nfr, nfc, nfr nfc, self-transpose То есть он ассоциативный, редуцированный и диагонально-симметричный. Покажу его раскрашенным. Но это, к сожалению, ЛК, а нас интересуют сейчас ДЛК. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А, кажется, поняла: на a вообще не надо обращать внимания, это какой-то просто символ вылез ненужный. И ДЛК будут такие 4 3 0 2 1 6 5 8 11 9 10 7 2 5 3 1 7 0 9 4 8 10 6 11 3 1 7 0 6 11 2 5 9 4 8 10 0 2 1 6 10 7 4 3 5 8 11 9 7 10 6 4 8 5 3 11 2 0 9 1 11 6 5 7 4 9 10 2 1 3 0 8 5 7 4 9 0 8 11 6 10 2 1 3 6 4 8 5 9 1 7 10 3 11 2 0 10 8 11 3 5 2 1 9 0 7 4 6 9 11 2 10 3 4 8 0 6 1 7 5 8 0 9 11 2 10 6 1 7 5 3 4 1 9 10 8 11 3 0 7 4 6 5 2 8 1 0 3 2 11 10 6 7 4 5 9 0 9 2 1 10 3 7 11 5 6 8 4 3 0 11 2 9 5 1 8 6 10 4 7 1 2 3 10 4 8 9 0 11 7 6 5 5 3 7 4 0 6 8 1 10 9 2 11 2 4 5 6 7 1 0 9 8 11 10 3 4 7 6 0 11 2 3 5 1 8 9 10 6 5 1 7 3 10 4 2 9 0 11 8 11 8 9 5 1 7 6 10 4 2 3 0 9 10 4 8 6 0 11 7 3 5 1 2 10 6 8 11 5 9 2 4 0 3 7 1 7 11 10 9 8 4 5 3 2 1 0 6 My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Это ДЛК 13-го порядка, построенный методом Гергели в моей статье http://www.natalimak1.narod.ru/dlk.htm  Поиск ортогональных ДЛК к этому ДЛК прервала (до конца о-ч-е-н-ь долго); найден всего один ортогональный соквадрат, вот он 9 0 3 2 5 1 8 6 4 A B 7 C 4 8 1 C 6 3 7 5 0 2 9 A B 6 2 7 0 4 A 9 3 C 1 5 B 8 8 A 0 5 3 B C 9 2 4 1 6 7 C 6 9 B A 2 5 4 3 7 8 0 1 1 7 5 4 B C A 2 8 3 0 9 6 5 C A 1 0 6 B 8 7 9 3 2 4 B 3 C 9 2 7 1 0 6 5 4 8 A A B 4 3 9 8 6 C 1 0 7 5 2 2 5 B 8 7 4 0 1 A 6 C 3 9 7 4 6 A 1 9 3 B 5 8 2 C 0 3 1 8 7 C 0 2 A 9 B 6 4 5 0 9 2 6 8 5 4 7 B C A 1 3 Ну, и то хорошо: не "пустышка". Ортогональную пару имеем. Далее обещала показать первый ЛК полной системы взаимно ортогональных ЛК 13-го порядка. Сейчас покажу. My new article "SOLS and SODLS" in Russian https://yadi.sk/d/nvdI6TgBrKv72A in English https://yadi.sk/d/VeY9bx6_q6CcZg |

©2026 (C) Progger