Вчера на форуме dxdy.ru в теме "Дьявольские магические квадраты" увидела статью 1914 г., выложил ссылку dmd, какой молодец!

Обалденный метод построения пандиагональных квадратов нечётного порядка!
Смотрите сами.
Я сейчас сделаю иллюстрацию для пандиагонального квадрата 7-го порядка из простых чисел.
Сразу замечу, что число 1 считается в статье простым числом. Ну, это не столь важно. Важен сам метод.

Иллюстрация готова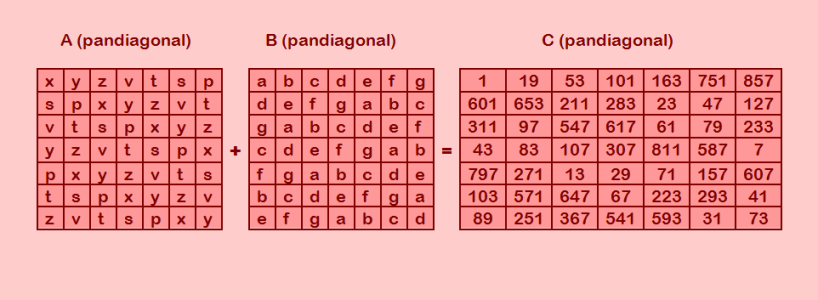



Кстати, я не увидела в статье картинку для квадрата 7-го порядка, есть картинка для квадрата 5-го порядка.
Для квадрата 7-го порядка приведён готовый пандиагональный квадрат С и значения символов, составляющих квадраты А и В.
Магическая константа квадрата S=1945.

Итак, что мы видим.
Есть два пандиагональных символьных квадрата А и В. Каждый из них составлен из 7 различных символов методом циклического сдвига (шаг циклического сдвига в квадратах разный).
Замечательные квадратики!
Символы квадрата А принимают значения простых чисел.
Символы квадрата В это смещения (или разности, как вам больше нравится).
Суммируя эти два квадрата, получаем пандиагональный квадрат С из простых чисел.
Грандиозно! Восторг! Красота! И это 1914 год!
Это же надо было так подобрать смещения!

Значения символов квадрата А и значения смещений, составляющих квадрат В, такие:

x=1, y=13, z=23, v=41, t=97, s=541, p=587
a=0, b=6, c=30, d=60, e=66, f=210, g=270

PS. Выше отмечено, что число 1 в статье считается простым.

Статья Россера появилась в 1939 году.
Методом Россера я построила минимальный (регулярный) пандиагональный квадрат 7-го порядка из простых чисел с магической константой S=1597.
Этот квадрат показан выше.
Пожалуй, продублирую его

191 89 397 409 43 157 311
379 103 101 491 17 313 193
317 241 109 163 439 47 281
223 383 227 107 541 37 79
331 337 7 139 167 563 53
83 347 389 277 127 307 67
73 97 367 11 263 173 613

Сейчас я его преобразую к более изящному виду и нарисую.
Мой квадрат несколько лучше квадрата из статьи.
Во-первых, он не содержит число 1, которое в настоящее время простым не считается.
Во-вторых, он имеет меньшую магическую константу.

PS. А вот весьма интересно, можно ли мой квадрат построить методом из статьи, показанным выше?
То есть подобрать 7 простых чисел и семь смещений так, чтобы составленные из них квадраты А и В в сумме дали мой квадрат.
Хороший вопрос!

Господа!
С этим можно поиграться даже вручную.
Головоломка :)
Ну, написать простенькую программку тоже можно.
При этом, разумеется, не обязательно строить мой пандиагональный квадрат.
Стройте любой квадрат из простых чисел, отличный от приведённого в статье.
И если у вас это получится... О! Если это получится... Это же будет алгоритм.

Минимальный (регулярный) дьявольский квадрат 7-го порядка из простых чисел


Магическая константа квадрата S=1597.
Я построила этот квадрат, Andersen доказал минимальность.

Примечание: дьявольский квадрат 7-го порядка называется регулярным, если ему соответствует квадрат Стенли (по преобразованию Россера).
С помощью квадрата Стенли этот квадрат и был построен.
Дьявольские квадраты 5-го порядка все регулярные.

PS. Некто очень давно окрестил пандиагональные квадраты дьявольскими.
Может быть, история и сохранила имя этого некто, но я не встречала это имя.
Как Белышев окрестил ОДЛК марьяжными :)
Термин прижился, уже иностранцы вовсю его используют (Томаш, Стефано).

Для дьявольского квадрата 5-го порядка покажу скриншот из статьи



Всё аналогично квадрату 7-го порядка.
Значения простых чисел и смещений такие:

x=1, y=13, z=23, v=41, t=97
a=0, b=6, c=30, d=60, e=66

Магическая константа построенного дьявольского квадрата 5-го порядка S=337.

Вчера очень долго думала, можно ли применить этот метод для построения дьявольского квадрата 5-го порядка из последовательных простых чисел.
Пока ничего не придумала.

Попытаюсь сформулировать задачу:
требуется найти 25 последовательных простых чисел

x, y, z, v, t, x+b, y+b, z+b, v+b, t+b, x+c, y+c, z+c, v+c, t+c, x+d, y+d, z+d, v+d, t+d, x+e, y+e, z+e, v+e, t+e

дающих в сумме число кратное 5.
Конечно, числа могут располагаться в другом порядке (в смысле возрастания).
Смещения a, b, c, d, e можно для начала взять те же самые, что приведены в статье. Однако можно взять и другие, только оставить a=0.
Вот и всё!
Но возможно ли это???
Как думаете, господа?
У меня уже мозги набекрень, все извилины заплела (по Высоцкому) :)

Вчера с коллегой Сергеем Беляевым перекинулись письмами.
Сергей, ау!
Давайте на помощь :)
Дьявольский квадрат 5-го порядка из последовательных простых чисел надо найти!
Такой маленький и до сих пор не найден.

Цитата

Попытаюсь сформулировать задачу:
требуется найти 25 последовательных простых чисел

x, y, z, v, t, x+b, y+b, z+b, v+b, t+b, x+c, y+c, z+c, v+c, t+c, x+d, y+d, z+d, v+d, t+d, x+e, y+e, z+e, v+e, t+e

дающих в сумме число кратное 5.

Кратность суммы всех чисел этой последовательности автоматически получается!
И не остаётся никаких условий.
Только все числа в этой последовательности должны быть 25-ю последовательными простыми числами.
И это всё!

Белышеву задание - найти такую последовательность :)
Хоть с такими же смещениями a, b, c, d, e, как приведено в статье, хоть с другими.
Подумалось: возможно, придётся добавить и смещение a≠0.

Кстати, вот пауза образовалась, и сразу же запустила поиск антимага25, немного покрутить до отбоя

Поиск антимага Стенли 5-го порядка               1:06:32
Текущий интервал: [538281411269416 ... 538283411269416]
Проверено:  3276%%
Скорость:    113 Всего: 58961213 Подходящих: 11792340

Работает, но... решения нет, нет и нет!

Это последний набор, выложенный Максом на форуме dxdy.ru

531511414105079: 0 18 30 42 48 90 102 132 144 150 182 200 212 272 282 290 302 314 332 338 422 440 464 470 524

От него я начала поиск по программе Белышева.
Не сильно продвинулась, потому что кручу программу очень редко по чуть-чуть.
Может быть, Макс и дальше искал, но сообщений о поиске и результатах я не видела.

Запостила головоломку на форуме у Томаша :)
https://boinc.tbrada.eu/forum_thread.php?id=3063

Вдруг там кто-то заинтересуется.
Лучше всего, если заинтересуется сам Томаш :)

Всё, прерываю программу

Поиск антимага Стенли 5-го порядка               3:44:32
Текущий интервал: [538581411147160 ... 538583411147160]
Проверено:  2432%%
Скорость:    113 Всего: 58969306 Подходящих: 11793920

Ничего не найдено.
Мы с черепашкой пойдём баиньки :)

Поигралась вручную с дьявольскими квадратиками 5-го порядка, улучшила результат, приведённый в статье, а именно: избавилась от 1, так как это не простое число.
Взяла x=167, значения всех остальных переменных остаются те же самые, какие в статье.
В результате получила такой пандиагональный квадрат 5-го порядка из простых чисел

167 19 53 101 163
71 157 233 13 29
79 23 47 127 227
103 197 73 89 41
83 107 97 173 43

Магическая константа этого квадрата S=503.

Итак, метод прекрасно работает!
Конечно, чтобы получить пандиагональный квадрат 5-го порядка из последовательных простых чисел, вручную поиграться - вряд ли оно получится.
Надо писать программу.

PS. В своё время Павловский построил много пандиагональных квадратов 5-го порядка из простых чисел, начиная с минимального и далее по возрастанию магической константы.
Вот нашла в файле с его решениями квадрат с магической константой S=503

503 = 11 17 23 29 31 41 43 47 61 67 79 83 89 97 103 107 113 127 139 163 167 179 197 239 263

После магической константы следует массив простых чисел, из которых квадрат построен.

А теперь посмотрите на массив простых чисел, из которых построен мой квадрат с той же магической константой

13 19 23 29 41 43 47 53 71 73 79 83 89 97 101 103 107 127 157 163 167 173 197 227 233

Массивы разные. Ну, в этом нет ничего удивительного.
А вот методы построения тоже резко отличаются.
Павловский строил квадраты методом Россера (из квадратов Стенли).
А я применила метод из статьи, показанной выше. Очень простой метод, мгновенно даёт решение, только чуть поколдовать с подбором значений для переменных в формуле. Это удаётся даже вручную.

Дублирую сообщение о моём решении, показанном в предыдущем посте, с форума проекта Tomas Brada, тут иллюстрация и всё наглядно

I will show two solutions in the illustration



At the top you see a solution from article, at the bottom you see my solution.

For the solution from the article

x=1, y=13, z=23, v=41, t=97
a=0, b=6, c=30, d=60, e=66

For my solution

x=167, y=13, z=23, v=41, t=97
a=0, b=6, c=30, d=60, e=66

I have an array from 25 primes

{13 19 23 29 41 43 47 53 71 73 79 83 89 97 101 103 107 127 157 163 167 173 197 227 233}

Ну, дело за маленьким: сделать то же самое, но! получить массив из 25 последовательных простых чисел.
Я написала бы простенькую программку и попробовала этот алгоритм.
Заковыка в том, что надо начинать с очень больших простых чисел, потому что для маленьких искать бесполезно, всё уже проверено и перепроверено.
А больших простых чисел у меня нету :(
И генерировать я их не могу непрерывно в программе. И Бейсик у меня с очень большими числами не работает.
Поэтому данный алгоритм попробовала только на маленьких простых числах, вручную.
Он работает, чёрт побери!

Это решение из статьи для квадрата 7-го порядка



тоже надо исправить, чтобы в пандиагональном квадрате не было числа 1.

Поиграйтесь, господа :) Это можно делать вручную.
А когда исправите это решение, займитесь задачей посложнее: получите пандиагональный квадрат 7-го порядка из последовательных простых чисел.
Не факт, что этот квадрат тоже будет в заоблачных высотах (как квадраты 4-го и 5-го порядков).
Как я уже отмечала, его ещё и не искали.
Вполне возможно, что он найдётся для небольших простых чисел, как нашёлся пандиагональный квадрат 6-го порядка.

А коллеги мои молчат :(
Ну, Макс вчера письмо прислал, хоть отписался, и за то спасибо.
Конечно, он не собирается искать какие-то там антимаги :) Всё в прошлом.
Были темы на форуме dxdy.ru, я работала над задачами и других увлекала.
Теперь темы остались, но меня нет. И все мои темы заглохли.
Но темы помнят!
Вот dmd не так давно ссылку выложил на классную статью в теме "Дьявольские магические квадраты".
Спасибо ему.

В теме "Симметричные кортежи из последовательных простых чисел" Петухов выкладывал новости проекта Stop@home.
Когда этот проект был остановлен, и Петухов замолчал.
А могли бы на пару с Бегемотом (Даниловым) и просчитать пропущенный в проекте интервал.
Да и дальше посчитать тоже могли бы. Проект какой-нибудь организовали бы.
Ну, а зачем? Меня нет на форуме и драйв у них пропал :)

Белышев и Progger даже отпиской не удостоят :(
Сергей Беляев пока тоже молчит, но мы с ним переписываемся, может, ещё ответит.

Carlos, приславший мне статью о пандиагональных квадратах 6-го порядка, спросил, не построила ли я пандиагональный квадрат 10-го порядка из простых чисел.
Я отправила ему построенный мной ассоциативный квадрат 10-го порядка из простых чисел, опубликованный здесь
https://dxdy.ru/post987797.html#p987797
Спросила его, известен ли ему метод преобразования ассоциативного квадрата чётного порядка в пандиагональный квадрат.
Он ответил, что известен.

А вот что он мне прислал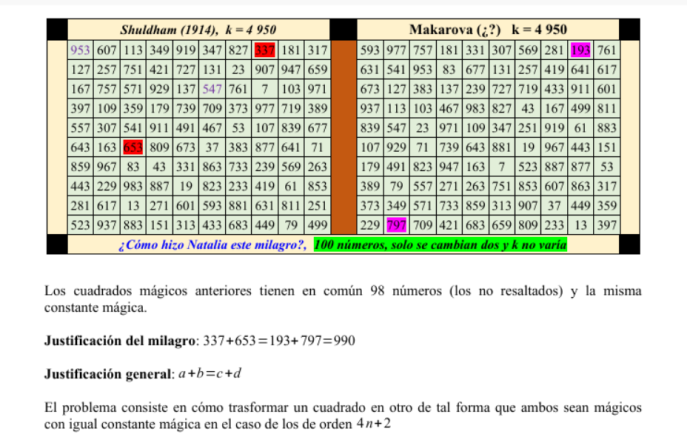


Поразительно! Эти два квадрата разделяет целый век (я построила квадрат в 2015 г.)!
Я, конечно, ничего не знала о приведённом пандиагональном квадрате 10-го порядка из простых чисел, построенном в 1914 г.
Построенный мной квадрат имеет такую же магическую константу и отличается от квадрата 1914 г. всего двумя числами (на иллюстрации они выделены).

Первый (известный нам - участникам форума dxdy.ru) пандиагональный квадрат 10-го порядка из простых чисел был построен Павловским, он опубликован на форуме.
Потом был конкурс, в котором Врублевский построил ещё ряд таких квадратов.
Например, самый последний из квадратов Врублевского с магической константой S=2850

(5,13,331,139,449,607,281,461,401,163),
(181,509,239,419,211,71,31,157,541,491),
(503,43,409,367,431,7,101,197,479,313),
(103,227,311,347,307,359,601,109,97,389),
(557,67,79,613,251,37,317,89,179,661),
(283,149,353,137,199,641,421,349,127,191),
(293,61,379,229,59,769,41,593,233,193),
(571,881,17,29,241,173,487,151,277,23),
(131,643,463,457,263,19,47,11,443,373),
(223,257,269,113,439,167,523,733,73,53)

http://74.72.151.186/Contest/PandiagonalMagicSquares/FinalReport

Цитата

Это решение из статьи для квадрата 7-го порядка



тоже надо исправить, чтобы в пандиагональном квадрате не было числа 1.

Кажется, у меня получилось.
Я взяла x=881, все остальные переменные с таким же значениями, как в статье.
Вот какой пандиагональный квадрат у меня получился

881 19 53 101 163 751 857
601 653 1091 283 23 47 127
311 97 547 617 941 79 233
43 83 107 307 811 587 887
797 1151 13 29 71 157 607
103 571 647 947 223 293 41
89 251 367 541 593 911 73

Магическая константа этого квадрата S=2825, он составлен только из различных простых чисел.
Вот этот массив

13  19  23  29  41  43  47  53  71  73  79  83  89  97  101  103  107  127  157  163  223  233  251  283  293  307  311  367  541  547  571  587  593  601  607  617  647  653  751  797  811  857  881  887  911  941  947  1091  1151

Итак, метод из статьи прекрасно работает и для порядка 7.
Можно ли этим методом составить пандиагональный квадрат 7-го порядка из последовательных простых чисел?
Хороший вопрос!
Кто хочет ответить? :)

Итак, вот решение методом из статьи для пандиагонального квадрата 5-го порядка

x=167, y=13, z=23, v=41, t=97
a=0, b=6, c=30, d=60, e=66

 +0 +6 +30 +60 +66
167 173 197 227 233
13 19 43 73 79
23 29 53 83 89
41 47 71 101 107
97 103 127 157 163

И что мы видим? Мы видим квадрат Стенли!
Оказывается, метод Россера зародился ещё в 1914 году.

Уф! Ну вот и чудесно. Значит, метод из статьи полностью эквивалентен построению пандиагонального квадрата 5-го порядка с помощью квадрата Стенли.

Метод из статьи фиксирует смещения для элементов первой строки квадрата Стенли.
В общем случае можно этого не делать.
Однако можно попробовать искать квадраты Стенли именно с такими смещениями. Это намного ускорит поиск, хотя не рассмотрит все квадраты Стенли 5-го порядка. Понятно, что решения при таком подходе могут быть пропущены. Зато намного выиграем в скорости.

Итак, что мы имеем на данный момент?
У меня сохранилась программа поиска квадрата Стенли 5-го порядка (Белышева), но нет исходного кода.
Нет также и описания программы.
Поэтому эта программа для меня (наверное, и не только для меня) представляет собой чёрный ящик, в котором неизвестно, что происходит.
Плохо ещё и то, что мы не можем программу протестировать, потому что у нас нет ни одного известного решения.
Естественно, крутить такую программу очень долго (без появления результатов) тоскливо.

Напрашивается вывод: либо надо получить информацию об этой программе Белышева, либо надо написать новую программу.
Оба выхода весьма трудные.
Алгоритм хорошо известен. Но... я не могу генерировать очень большие простые числа, да ещё и Бейсик у меня с большими числами не работает.
Получить информацию от Белышева (описание, исходный код) о-ч-е-н-ь проблематично.

И что же делать? Думаю вот усиленно, пока ничего не придумала :(

PS. То, что просчитал М. Алексеев по своей программе, тоже не стопроцентно, он также мог ошибиться в программе. Нет независимых результатов, результатов по этой задаче вообще нет.

Выше я спрашивала, можно ли построить пандиагональный квадрат 7-го порядка, построенный мной с помощью квадрата Стенли, методом из статьи.
Да, можно! Теперь уже никаких сомнений не осталось.
Покажу иллюстрацию, на которой всё ясно без слов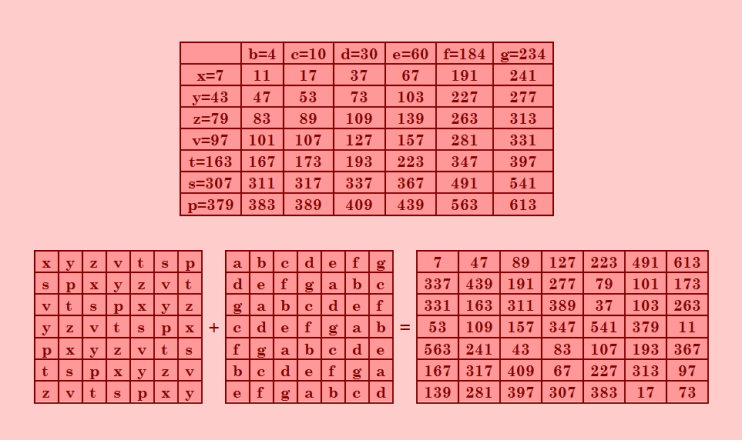



Сверху квадрат Стенли, внизу соответствующее построение методом из статьи.

Не сразу я увидела в методе из статьи метод построения с помощью квадрата Стенли, но лучше поздно, чем никогда.
Сейчас всё стало понятно.
Остаётся написать программу и поискать пандиагональные квадраты 5-го и 7-го порядков из последовательных простых чисел.
При этом можно зафиксировать смещения при построении квадратов Стенли, то есть взять их из статьи. Эти смещения наиболее благоприятны, однако... они дадут кучу пропущенных квадратов Стенли.
Из двух зол выбирают меньшее :)
Обратите внимание на смещения в построенном мной квадрате Стенли, они не такие, как в статье, но смещения 30 и 60 присутствуют.

Напомню сообщение Andersen о паттернах для квадратов Стенли 5-го порядка из последовательных простых чисел

The smallest admissible width for a Stanley antimagic square with n=5 is 156 for these four patterns:

0 30 60 84 114
2 32 62 86 116
6 36 66 90 120
20 50 80 104 134
42 72 102 126 156

0 14 30 44 54
6 20 36 50 60
42 56 72 86 96
90 104 120 134 144
102 116 132 146 156

0 12 60 96 102
10 22 70 106 112
24 36 84 120 126
40 52 100 136 142
54 66 114 150 156

0 30 54 84 114
22 52 76 106 136
36 66 90 120 150
40 70 94 124 154
42 72 96 126 156

None of them have an occurrence below 10^20 and finding 25 simultaneous primes is infeasible. The largest known non-trivial prime k-tuplets are 19-tuplets found by Raanan Chermoni & Jaroslaw Wroblewski. 25 may be millions of times harder.

It also looks infeasible to find n=5 by generating consecutive primes and testing them. The jump in complexity from n=4 to n=5, i.e. from 16 to 25 primes, is just too hard.

https://dxdy.ru/post845503.html#p845503
Это вам готовые шаблоны для поиска квадратов Стенли 5-го порядка из последовательных простых чисел.
Но... это не совсем хорошие шаблоны, потому что, как пишет Andersen, последовательности из простых чисел, соответствующие этим шаблонам, не встречаются до 10^20.
Хотя, например, для Врублевского это не очень страшно :)
Он работает и с 21- и с 22-значными простыми числами и, возможно, больше.
Для меня - да, это страшно большие числа. Я с такими не могу работать.

Эти паттерны, как я понимаю, с минимальным диаметром 156.
Но нам не обязательно иметь минимальный диаметр, нам приемлем любой диаметр, лишь бы квадрат Стенли составился (из последовательных простых чисел).