Покажу иллюстрацию для пандиагонального квадрата 8-го порядка из последовательных простых чисел с 4 "дырками"



Этот квадрат я искала 2 месяца. Первые приближения содержали 14 "дырок". Потом была упорная оптимизация, что дало решение с 4 "дырками".
Найти точное решение очень трудно.
Я писала об этой задаче Врублевскому, когда только начинала её решать; в тот момент у меня было приближение с 11 "дырками".
Вот что он мне ответил:

Ja dumaju, czto najti kwadrat 8x8 s priedpolozenym naborom czisel prakticzeski niewozmozno. Pomnitie, czo dla kwadrata 7x7 eto bylo oczen oczen slozno, dla kwadrata 8x8 eto jeszczio sloznieje. No 11 dyrok eto sowsiem mnogo - mnie kazetsja, czto eto mozno umienszit (no nie k nuliu).

(из моего сообщения https://dxdy.ru/post939437.html#p939437 )
Да, разумеется, из предложенного набора простых чисел пандиагональный квадрат 8-го порядка построить вряд ли возможно. Я билась два месяца и... квадрат не составился.
Но мне всегда интересны приближённые решения (решения с ошибками, или с "дырками").
По этим решениям я вижу, насколько можно приблизиться к точному решению.
Да, найти набор из 64 последовательных простых чисел, из которых составится пандиагональный квадрат 8-го порядка, чрезвычайно трудно.
Это пока не удалось даже для квадрата 5-го порядка, для которого нужен набор всего из 25 последовательных простых чисел.

Господа!
Убедительная просьба: если кто-то решал/решает эту проблему или встречал в Интернете что-нибудь об этой проблеме, сообщите, пожалуйста.
Я давно не занимаюсь магическими квадратами и не слежу за проблемой в Сети.
По дьявольским квадратам в 2013 г. был проведён международный конкурс у Al Zimmermann (по моей инициативе).
В этом конкурсе искали дьявольские квадраты из простых чисел (не последовательных).
Замечательные решения были получены в конкурсе Я. Врублевским, он занял первое место.
К сожалению, ссылка на конкурс
http://www.azspcs.net/Contest/PandiagonalMagicSquares
сейчас не работает.

На dxdy.ru пишут, что это проблемы с сервером и пока можно войти на сайт по этой ссылке
http://74.72.151.186/
Да, действительно, можно войти на сайт, я проверила.
Войдите на сайт и найдёте там конкурс PandiagonalMagicSquares.

О!
Получила статью из Испании о пандиагональных квадратах 6-го порядка.
Показываю начало статьи



Дальше есть весьма интересная формула пандиагонального квадрата 6-го порядка L. S. Pierson, 1917 г. Пока не вникала в эту формулу.
Я выложу статью в Облако на mail.ru.
Статья может оказаться полезной при поиске следующих (за единственным известным) пандиагональных квадратов 6-го порядка из последовательных простых чисел.

Приятно удивило, что в статье приведены мои результаты.

Выложу ещё скриншот с формулой пандиагонального квадрата 6-го порядка, чтобы не забыть (статью выложить могу забыть)



Чтобы разобраться с формулой, надо делать перевод текста. Пока нет времени, может быть, позже дойдут руки.
Сейчас занялась общей формулой пандиагонального квадрата 7-го порядка.
Хочу попробовать проверку потенциальных массивов по этой формуле.
Для пандиагональных квадратов 7-го порядка не надо строить квадраты Стенли.
Дело в том, что пандиагональные квадраты 7-го порядка получаются не только из квадратов Стенли.
Поэтому тут лучше искать сразу пандиагональный квадрат, а не квадрат Стенли.

Копирую с конкурса замечательное решение Я. Врублевского - минимальный пандиагональный квадрат 7-го порядка из простых чисел (не последовательных!), магическая константа квадрата S=733 (минимальная)

(3,7,173,223,17,197,113), (181,211,11,79,131,23,97), (43,41,149,89,137,191,83), (233,103,107,73,127,31,59), (29,167,101,19,199,67,151), (5,47,139,179,109,61,193), (239,157,53,71,13,163,37)

отсюда
http://74.72.151.186/Contest/PandiagonalMagicSquares/FinalReport

Врублевский искал это решение очень долго уже после окончания конкурса (и не он один искал; он даже выкладывал для всех свою программу поиска). И нашёл он решение 10 октября 2013 г.
Смотрите статью в OEIS, посвящённую минимальным пандиагональным квадратам из простых чисел
http://oeis.org/A179440
A179440 The smallest magic constant of pan-diagonal magic squares which consist of distinct prime numbers
240, 395, 450, 733

Начинаются пандиагональные магические квадраты с порядка 4.
В статье мы видим всего 4 члена, соответствующие квадратам порядков 4 - 7.

Вот на квадрате Врублевского 7-го порядка буду проверять общую формулу.
Сейчас занимаюсь выбором наиболее оптимального варианта написания программы расчётов по этой формуле.
Я покажу этот замечательный квадрат в привычном виде.

Эх, Макса очень не хватает.
Он специалист по оптимизации общих формул магических квадратов.
Я написала ему письмо и пригласила в тему для обсуждения и решения проблемы.
Белышева тоже не хватает.
Мы в то время на форуме dxdy.ru жарко обсуждали с ним метод построения пандиагональных квадратов 7-го порядка.
Недавно читала это обсуждение. Там метод точных покрытий. Прекрасный метод! Белышевым предложен.
Я даже писала программу для нахождения точных покрытий квадрата 7-го порядка (и не только!). Но... это было так давно. Надо всё вспоминать и заново писать программу.
Ну, Белышева уже давным-давно приглашаю на форум.
Тут ведь все темы ему хорошо знакомы! Всё начинали вместе. Так хорошо начинали.

Сергея Беляева тоже надо вытащить. Но как вытащить? :(
Кстати, Сергей вывел свою замечательную формулу для построения пандиагональных квадратов 6-го порядка.

Макс, Алексей, Сергей, я жду вас!
Вспомните, как мы работали. Давайте продолжим.

Вот знаменитый минимальный пандиагональный квадрат 7-го порядка из простых чисел, найденный Врублевским



Напомню, что простые числа, из которых составлен этот квадрат, не последовательные.
Теперь надо найти пандиагональный квадрат 7-го порядка из последовательных простых чисел, конечно, желательно минимальный.
Но если найдётся хоть какой-нибудь, тоже будет здорово.
Как следует такой квадрат никто не искал, по-моему (кроме меня, конечно).
Мы тогда застряли на квадрате 5-го порядка, который так и не нашли.
Ну, а у меня это лучшее приближение с 4 "дырками"

151 139 227 181 13 79 7
43 11 73 157 49* 253* 211
167 137 97 193 23 31 149
107 109 131 113 199 97* 41
173 101 59 17 197 71 179
53 239 127 89 233 37 19
103 61 83* 47 83 229 191

Труднее ли решить задачу для квадрата порядка 7, чем для квадрата порядка 5?
Сложно сказать. Ведь для квадрата порядка 6 решение нашлось давно, причём минимальное.
Надо искать. Искать не будем - точно не найдём :)

Своё решение тоже покажу, переставила в нём столбцы, так изящнее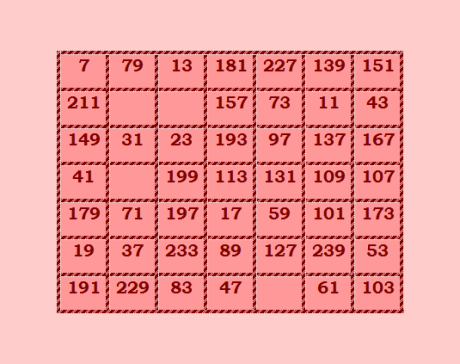



"Дырки" наглядные.

Итак, господа!
Решение без "дырок" в студию! :)

Дорогой Алексей!
Пожалуйста, напишите программу поиска пандиагонального квадрата 7-го порядка методом точных покрытий.
У вас это получится гораздо лучше, чем у меня.
Да и программу поиска антимага25 надо бы попробовать оптимизировать, всё-таки скорость оставляет желать много лучшего.

Кстати, я немножко (в перерывах) кручу эту программу.
Сейчас работает

Поиск антимага Стенли 5-го порядка              11:05:38
Текущий интервал: [535477412398926 ... 535479412398926]
Проверено:  5686%%
Скорость:    113 Всего: 58976703 Подходящих: 11798854

Никаких выходных файлов не появляется. Нет решения - хоть застрелись :(
Надо в BOINC-проект задачу поставить :) Точно найдём решение.
Кто готов запустить?

Progger
ау! Вы не готовы? :)
Ах, а кстати... вы же писали программу поиска квадрата Стенли 5-го порядка. Она сохранилась?

Выкладываю полученную сегодня статью из Испании о пандиагональных квадратах 6-го порядка
https://cloud.mail.ru/public/5fJN/4knFCmd3b

Но... у меня в компьютере статья не открывается, расширение у файла странное, у меня файлы с таким расширением не открываются (нет соответствующей программы).
В почте (в Яндексе) просматривать могу прикреплённую статью.

Начала писать программу поиска пандиагонального квадрата 7-го порядка по общей формуле.
Ох, как же давно я не писала программы для магических квадратов!
Уж и не знаю, что у меня получится сейчас :)
Общую формулу раскопала в архиве. Она была получена в каком-то матпакете или в онлайн-решателе (по составленной мной системе уравнений) участником форума ПЕН (форум приказал нам долго жить), где я много писала о магических квадратах. Участник этот (12d3) и на форуме dxdy.ru немного участвовал в моих темах о магических квадратах.
Формула нормальная, я её тогда проверяла. Но для составления программы надо выбрать оптимальный порядок расчётов.
Вот сижу колдую :)
Построение пандиагонального квадрата 7-го порядка по общей формуле выполняется очень долго.
Даже и для пандиагональных квадратов 5-го порядка это долго.
Вот почему для порядка 5 мы искали квадраты Стенли, эти квадраты строятся намного быстрее, чем пандиагональные квадраты.
Однако, как уже отмечено выше, для порядка 7 поиск пандиагональных квадратов через квадраты Стенли не годится.
Множество всех квадратов Стенли 7-го порядка не даёт всего множества пандиагональных квадратов.

Вот из-за того, что поиск по общей формуле очень долгий, я и прошу Белышева попробовать поиск методом точных покрытий.
Вполне возможно, что это будет быстрее.

С головой ушла в программу; трудно пишется, но всё-таки двигается к завершению.

Господа!
Я покажу общую формулу дьявольского квадрата 7-го порядка, как только закончу писать программу.

PS. Последнее полученное программой заполнение квадрата (тестирую программу по квадрату Врублевского)

163  79  59  199  13  107  113 
 0  211  127  53  0  0  11 
 181  71  157  31  137  73  83 
 0  17  97  67  0  0  139 
 61  223  101  103  89  5  151 
 0  109  0  149  7  3  193 
 0  23  0  131  167  239  43 

S= 733
Где нули стоят, это ещё не посчитанные элементы. Среди них есть один свободный, остальные зависимые.

Уф!
Программу написала, квадрат Врублевского она строит.

Итак, смотрим общую формулу.
Это дьявольский квадрат 7-го порядка в общем виде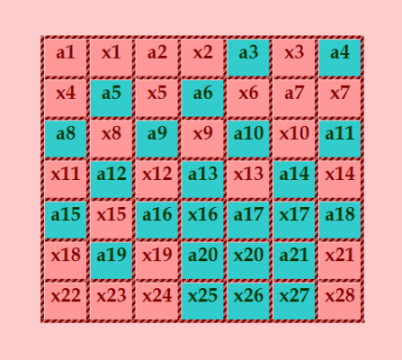



то есть все его элементы записаны в виде переменных.
Почему ячейки по-разному раскрашены?
Всё просто: в зелёных ячейках находятся свободные переменные, а в красных ячейках зависимые переменные.
Так их распределил онлайн-решатель.
Формула получилась типа 24+25, то есть 24 свободных переменных и 25 зависимых.

А теперь представьте: есть массив из 49 чисел (массив мы задаём точно из 49 чисел, так как собираемся строить дьявольские квадраты из последовательных простых чисел).
Каждая свободная переменная, записанная в квадрате, может принять любое значение из этого массива.
Зависимые переменные вычисляются при некотором раскладе свободных переменных. Если расчёт не дал требуемый результат, перебор свободных элементов продолжается.
Таким образом, в моей программе реализован хорошо известный алгоритм - перебор с возвратом.
Но! При этом очень много зависит от выбора порядка перебора свободных элементов и порядка вычисления зависимых переменных.
Это и называется оптимизацией обшей формулы магического квадрата.
Макс Алексеев много занимался этим. У него вроде даже была программа для автоматической оптимизации, насколько помню.

Далее покажу общую формулу дьявольского квадрат 7-го порядка в соответствии с переменными, показанными на иллюстрации.

Общая формула пандиагонального магического квадрата 7-го порядка

x1 -> -a11 + a12 + a13 + a15 + a16 + a17 + a20 + a21 - a4 + a5 + 
a6 + a8 + a9 - 2 S + x16 + x17 + x20 + x25 + x26 + x27,
x2 -> a12 - a18 - a4 + a5 + a8 + a9 - x16,
x3 -> a10 + a11 - a12 + a18 - a20 - a21 + a4 - a5 - a8 + S - x17 - 
x20 - x25 - x26 - x27,
x4 -> a10 + a12 + a13 + a16 + a19 + a9 - x16 - x17 - x20 - x25 - x27,
x5 -> a10 + a11 - a21 + a3 + a4 - a5 - x17,
x6 -> a13 + a14 + a16 + a17 + a18 + a20 + a21 - a3 - S + x16 + x17,
x7 -> -a10 - a11 - a16 - a18 + a21 - a4 + a5 + x17 + x20 + x25 + x27,
x8 -> -a10 - a12 - a13 - a16 - a17 - a19 - a20 - a21 - a5 - a8 - 
a9 + 2 S - x20 - x26,
x9 -> -a12 - a13 + a18 - a20 + a4 - a5 - a6 - a8 - a9 + S - x25,
x10 -> -a11 + 2 a12 + 2 a13 + a16 + a17 - a18 + a19 + 2 a20 + a21 - 
a4 + 2 a5 + a6 + a8 + a9 - 2 S + x20 + x25 + x26,
x11 -> -a11 + a13 + a16 + a17 + a19 + a20 + a21 - a3 + a5 - S + 
x16 + x17 + x20,
x12 -> a17 + a20 + a21 - a4 + a5 + a8 - S + x17 + x20 + x25 + x26,
x13 -> -a10 - a13 - a14 - a16 - 2 a17 - a18 - a20 - a21 + 2 S - 
x16 - x17 - x20 - x26,
x14 -> a10 + a11 - a12 - a13 + a18 - a19 - a20 - a21 + a3 + a4 - 
2 a5 - a8 + S - x17 - x20 - x25,
x15 -> -a15 - a16 - a17 - a18 + S - x16 - x17,
x18 -> -a10 - a13 - a14 - a16 - a17 - a18 - a19 - a20 - a21 + a3 + 
S + x25 + x27,
x19 -> a10 + a12 + a13 + a14 + a15 + a16 + a17 + a18 + a6 + a9 - S -
x20 - x25,
x21 -> -a12 - a15 - a3 - a6 - a9 + S - x27,
x22 -> a12 + a13 + a14 + a17 + a20 + a21 - a4 + a5 + a6 + a9 - S,
x23 -> a10 + a11 - a12 + a16 + a17 + a18 + a4 - a5 - a6 - x25 - x27,
x24 -> -a10 - 2 a12 - 2 a13 - a14 - a15 - 2 a16 - 2 a17 - a19 - 
2 a20 - a21 + a4 - a5 - a6 - a8 - 2 a9 + 3 S - x26,
x28 -> -a11 + 2 a12 + a13 + a15 + a16 - a18 + a19 + a20 - a4 + a5 + 
a6 + a8 + a9 - S,
a1 -> a11 - 2 a12 - 2 a13 - a15 - a16 - a17 + a18 - a19 - a20 - 
a21 + a4 - 2 a5 - a6 - a8 - 2 a9 + 2 S,
a2 -> -a10 - a11 + a12 + a13 - a18 + a19 + a20 + a21 - a3 - a4 + a5,
a7 -> -a10 - a12 - 2 a13 - a14 - a16 - a17 - a19 - a20 - a21 - a5 - 
a6 - a9 + 2 S

Здесь ещё присутствует магическая константа квадрата S, она у нас известна, так как мы задаём массив точно из 49 чисел.

Примечание: знак -> означает знак равенства.

Итак, попробуйте написать поиск пандиагонального квадрата 7-го порядка по общей формуле.
Попытайтесь оптимизировать формулу.
Посмотрите, сколько будет строиться квадрат из заданного массива из 49 последовательных простых чисел.
Это будет очень долго!
Врублевский искал свой квадрат много суток (при непрерывных расчётах).
Разумеется, такой поиск для пандиагональных квадратов 7-го порядка из последовательных простых чисел никуда не годится.

Ну, кто знает, вдруг вам удастся так оптимизировать программу, что она будет строить квадрат хотя бы за 2-3 часа, то есть проверять, строится квадрат или нет для заданного массива.
Тогда ещё можно что-то поискать.
Но если один квадрат будет строиться несколько суток, поставленную задачу решить нереально.

Посмотрим ещё раз на минимальный пандиагональный квадрат 7-го порядка из простых чисел, найденный Врублевским



Это массив из 49 простых чисел (не последовательных!), из которых составлен данный квадрат

3  5  7  11  13  17  19  23  29  31  37  41  43  47  53  59  61  67  71  73  79  83  89  97  101  103  107  109 113  127  131  137  139  149  151  157  163  167  173  179  181  191  193  197  199  211  223  233  239 

Кстати, в массиве пропущены всего два простых числа: 227 и 229.
Квадрат почти из последовательных простых чисел!

Важные подсказки.
1. Магическая константа квадрата S находится просто: надо найти сумму всех 49 чисел массива и поделить её на 7.
Отсюда возникает необходимое условие, которому должен удовлетворять массив из 49 чисел: сумма всех чисел массива должна быть кратна 7.
Для квадрата Врублевского имеем: сумма всех чисел массива равна 5131, а магическая константа квадрата
S = 5131/7 = 733

2. Насчёт перебора свободных переменных.
Пандиагональный квадрат можно перенести на торе так, что, например, в его левой верхней ячейке будет стоять любое число (без потери пандиагональности квадрата).
Поэтому без нарушения общности можно считать, что элемент в этой ячейке нам уже задан, то есть мы его фиксируем (это может быть любое число массива).
Это даёт возможность сократить перебор на одну переменную. Таким образом, остаются для перебора 23 свободных переменных.

Первый подходящий (для пандиагонального квадрата 7-го порядка) массив из 49 последовательных простых чисел

7  11  13  17  19  23  29  31  37  41  43  47  53  59  61  67  71  73  79  83  89  97  101  103  107  109 113  127  131  137  139  149  151  157  163  167  173  179  181  191  193  197  199  211  223  227  229  233  239 

Из этого массива я и пыталась построить пандиагональный квадрат, но это у меня не получилось.
Выше показано приближённое решение с 4 "дырками".
Однако не факт, что решения для данного массива точно не существует. Это не доказано.
Просто моя программа не смогла найти решение.

Для данного массива имеем: сумма всех чисел массива равна 5579, а магическая константа квадрата
S = 5579/7 = 797

Легко можно найти следующие потенциальные (подходящие) массивы из 49 последовательных простых чисел.
Каждый такой массив надо проверить на предмет построения пандиагонального квадрата 7-го порядка.
А вот проверка-то... ой... может растянуться на годы при существующем ПО.
Значит, нужно придумать более совершенное ПО.
В крайнем случае, можно попробовать поиск и через квадраты Стенли. Какой-нибудь пандиагональный квадрат из последовательных простых чисел можно найти, но он может оказаться, скорее всего, не минимальным.

Покажу пример.
Это квадрат Стенли 7-го порядка из простых чисел (не последовательных), построенный мной

7 11 17 37 67 191 241
43 47 53 73 103 227 277
79 83 89 109 139 263 313
97 101 107 127 157 281 331
163 167 173 193 223 347 397
307 311 317 337 367 491 541
379 383 389 409 439 563 613

Andersen доказал, что это минимальный квадрат Стенли из простых чисел.
Из квадрата Стенли с помощью преобразования Россера получаем пандиагональный квадрат 7-го порядка из простых чисел с магической константой S=1597

191 89 397 409 43 157 311
379 103 101 491 17 313 193
317 241 109 163 439 47 281
223 383 227 107 541 37 79
331 337 7 139 167 563 53
83 347 389 277 127 307 67
73 97 367 11 263 173 613

Но! Это не минимальный квадрат 7-го порядка из простых чисел.
Минимальный квадрат показан выше, его нашёл Врублевский по другому алгоритму (не используя квадраты Стенли).

Однако если квадраты Стенли 7-го порядка будут строиться шустро, можно их попытать.
Пусть хотя бы не минимальный пандиагональный квадрат из последовательных простых чисел найдётся. Пока нет никакого.

PS. И вот у меня в рабочем файле записано преобразование Россера (в матричной форме), превращающее квадрат Стенли 7-го порядка в пандиагональный квадрат

a16 a33 a57 a74 a21 a45 a62
a71 a25 a42 a66 a13 a37 a54
a63 a17 a34 a51 a75 a22 a46
a55 a72 a26 a43 a67 a14 a31
a47 a64 a11 a35 a52 a76 a23
a32 a56 a73 a27 a44 a61 a15
a24 a41 a65 a12 a36 a53 a77

Полезное преобразование.
На приведённом выше примере можно проверить.

Итак, задача-минимум: найти хотя бы один (любой!) квадрат Стенли 7-го порядка из последовательных простых чисел.
Пишем программу для проверки массива из 49 чисел на предмет построения квадрата Стенли, то есть антимага49 :)
И вперёд!

Кстати, здесь
https://www.primepuzzles.net/puzzles/puzz_681.htm
опубликована общая формула квадрата Стенли 7-го порядка от Andersen

d=7, X50=S, e=37

x1 = - x14 - x21 - x28 - x35 - x42 - x44 - x45 - x46 - x47 - x48 + 4 x49 + x50
x2 = - x14 - x21 - x28 - x35 - x42 - x43 - x45 - x46 - x47 - x48 + 4 x49 + x50
x3 = - x14 - x21 - x28 - x35 - x42 - x43 - x44 - x46 - x47 - x48 + 4 x49 + x50
x4 = - x14 - x21 - x28 - x35 - x42 - x43 - x44 - x45 - x47 - x48 + 4 x49 + x50
x5 = - x14 - x21 - x28 - x35 - x42 - x43 - x44 - x45 - x46 - x48 + 4 x49 + x50
x6 = - x14 - x21 - x28 - x35 - x42 - x43 - x44 - x45 - x46 - x47 + 4 x49 + x50
x7 = - x14 - x21 - x28 - x35 - x42 - x43 - x44 - x45 - x46 - x47 - x48 + 5 x49 + x50
x8 = x14 + x43 - x49
x9 = x14 + x44 - x49
x10 = x14 + x45 - x49
x11 = x14 + x46 - x49
x12 = x14 + x47 - x49
x13 = x14 + x48 - x49
x15 = x21 + x43 - x49
x16 = x21 + x44 - x49
x17 = x21 + x45 - x49
x18 = x21 + x46 - x49
x19 = x21 + x47 - x49
x20 = x21 + x48 - x49
x22 = x28 + x43 - x49
x23 = x28 + x44 - x49
x24 = x28 + x45 - x49
x25 = x28 + x46 - x49
x26 = x28 + x47 - x49
x27 = x28 + x48 - x49
x29 = x35 + x43 - x49
x30 = x35 + x44 - x49
x31 = x35 + x45 - x49
x32 = x35 + x46 - x49
x33 = x35 + x47 - x49
x34 = x35 + x48 - x49
x36 = x42 + x43 - x49
x37 = x42 + x44 - x49
x38 = x42 + x45 - x49
x39 = x42 + x46 - x49
x40 = x42 + x47 - x49
x41 = x42 + x48 - x49

Количество свободных переменных в этой формуле равно 13.
Сравните с общей формулой пандиагонального квадрата. Там 24 свободные переменные!
Поэтому квадрат Стенли строится в разы быстрее, нежели пандиагональный квадрат.

X50=S - это индекс квадрата Стенли.
Если мы будем строить квадрат Стенли из массива, состоящего точно из 49 чисел, индекс S в этом случае известен.

PS. Квадрат Стенли записывается с переменными xi в следующем виде

x1 x2 x3 x4 x5 x6 x7
x8 x9 x10 x11 x12 x13 x14
x15 x16 x17 x18 x19 x20 x21
x22 x23 x24 x25 x26 x27 x28
x29 x30 x31 x32 x33 x34 x35
x36 x37 x38 x39 x40 x41 x42
x43 x44 x45 x46 x47 x48 x49

Важное замечание
Любая перестановка строк/столбцов в квадрате Стенли снова даёт квадрат Стенли.
Поэтому не нарушая общности можно зафиксировать элемент x1, например, присвоив ему минимальное число заданного массива.
Это уменьшает число свободных переменных на одну.

Посмотрите на построенный мной квадрат Стенли 7-го порядка из простых чисел

7 11 17 37 67 191 241
43 47 53 73 103 227 277
79 83 89 109 139 263 313
97 101 107 127 157 281 331
163 167 173 193 223 347 397
307 311 317 337 367 491 541
379 383 389 409 439 563 613

Элемент x1 у меня зафиксирован в программе, это минимальное число массива.

PS. В формуле Andersen зафиксировать надо переменную x49, потому что переменная x1 у него не свободная, а зависимая.
Итак, переменную x49 фиксируем, переменная x50 (индекс квадрата Стенли) у нас известна, и в формуле Andersen остаётся всего 11 свободных переменных:
x14, x21, x28, x35, x42, x43, x44, x45, x46, x47, x48

Если программу будет писать Белышев, он управится с 6 свободными переменными :)
В программе поиска антимага25 у него 4 свободные переменные!
Этого достаточно. чтобы установить, что квадрат Стенли из заданного массива не построится.

А вот здесь
https://dxdy.ru/post577600.html#p577600
общая формула квадрата Стенли 7-го порядка от Someone.
Это в моей теме "Антимагические квадраты" на форуме dxdy.ru.
Интересно, что она в точности совпадает с формулой Andersen. Наверное, решали систему уравнений в одном матпакете.
Ну, тем лучше: две формулы, полученные независимо. Значит, всё уже точно.
Можно брать формулу на вооружение и писать программу поиска квадрата Стенли 7-го порядка.