Двушки и узорчатые ДЛК
Message boards :
Science :
Двушки и узорчатые ДЛК
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Посмотрим на двушки с точки зрения узорчатых ДЛК. Раньше я не очень обращала внимание на двушки в этом аспекте. Сейчас выполняла постобработку алгоритмом поворота блоков, нашла очень симпатичную двушечку 0 1 2 3 4 5 6 7 8 9 6 7 8 4 9 1 3 5 2 0 3 4 5 1 2 7 9 8 0 6 2 9 4 6 0 8 1 3 5 7 9 5 1 7 3 0 8 4 6 2 1 8 9 2 6 4 7 0 3 5 7 0 3 5 8 9 2 6 1 4 8 6 7 9 5 2 0 1 4 3 5 3 0 8 7 6 4 2 9 1 4 2 6 0 1 3 5 9 7 8 sq1 0 1 2 3 4 5 6 7 8 9 6 7 8 4 9 1 3 5 2 0 3 4 5 1 2 7 9 8 0 6 2 9 4 6 0 8 1 3 7 5 9 5 1 7 3 0 8 4 6 2 1 8 9 2 6 4 5 0 3 7 7 0 3 5 8 9 2 6 1 4 8 6 7 9 5 2 0 1 4 3 5 3 0 8 7 6 4 2 9 1 4 2 6 0 1 3 7 9 5 8 sq2 Square: 0 1 2 3 4 5 6 7 8 9 1 2 3 0 6 9 5 8 4 7 8 6 9 4 7 3 2 1 5 0 6 3 7 5 9 2 8 4 0 1 5 4 0 9 1 6 7 2 3 8 7 5 4 1 2 8 0 3 9 6 4 8 6 7 0 1 3 9 2 5 9 7 5 8 3 0 4 6 1 2 2 0 1 6 8 4 9 5 7 3 3 9 8 2 5 7 1 0 6 4 БД ручного проекта я веду в первом формате; так начинала, так и продолжаю, мне так удобнее. Ну вот, двушка эта полновесная и узорчатые ортогональные соквадраты налицо. Иллюстрацию сделала во втором формате  Чудесные ортогональки! Сравните с троечкой  |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А это показанные тут https://boinc.progger.info/odlk/forum_thread.php?id=46&postid=3474#3474 полновесные двушки-близняшки 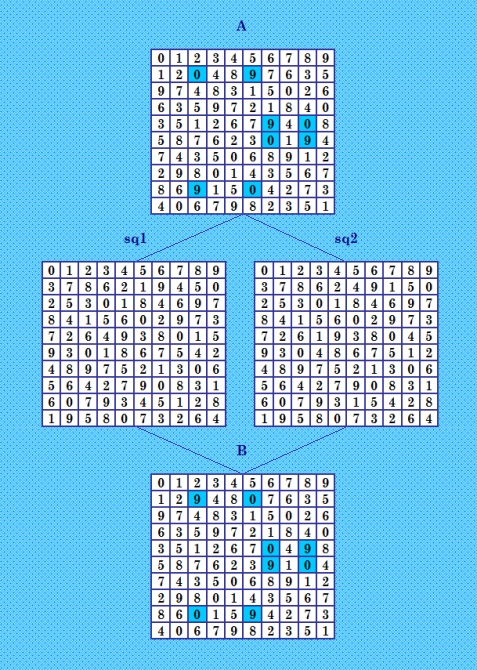 Основные ДЛК двушек узорчатые (преобразование - поворот блоков), ортогональки двушек тоже узорчатые (преобразование - поворот блоков)! Очень милые двушечки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Недавно найденная XAVER в моём новом эксперименте двушка  Сравните с двушкой отсюда https://boinc.progger.info/odlk/forum_thread.php?id=137&postid=4585#4585 Очень уж похожий тип узорчатости ортогональных соквадратов в обеих двушках. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот двушечка, моя самая первая, я нашла её давным-давно алгоритмом случайного перебора (генератор был В. Чиркова, а программа поиска ОДЛК С. Беляева)  В то время не рассматривала ещё узорчатые ДЛК. Посмотрите на ортогональные соквадраты этой двушки. А это от того же ДЛК получила ортогональные соквадраты программой Белышева [DLK(2)] 0 1 2 3 4 5 6 7 8 9 8 6 7 4 1 3 5 9 0 2 9 5 3 8 2 0 1 6 7 4 2 7 8 9 0 6 4 5 1 3 7 4 0 6 5 2 3 1 9 8 3 2 6 1 8 7 9 4 5 0 4 0 9 7 6 1 8 3 2 5 6 8 1 5 9 4 0 2 3 7 1 3 5 0 7 9 2 8 4 6 5 9 4 2 3 8 7 0 6 1 [mate#1] 5 3 8 4 2 1 6 7 9 0 6 0 5 3 9 2 8 4 1 7 7 2 9 0 4 6 1 8 3 5 2 9 3 1 0 7 4 5 6 8 8 7 4 5 6 9 3 0 2 1 0 1 2 8 5 4 9 6 7 3 9 8 6 2 3 5 7 1 0 4 1 4 7 9 8 0 2 3 5 6 4 6 0 7 1 3 5 2 8 9 3 5 1 6 7 8 0 9 4 2 [mate#2] 5 3 8 4 2 1 6 7 9 0 6 0 5 3 8 2 9 4 1 7 7 2 9 0 4 6 1 8 3 5 2 9 3 1 0 7 4 5 6 8 8 7 4 5 6 9 3 0 2 1 0 1 2 9 5 4 8 6 7 3 9 8 6 2 3 5 7 1 0 4 1 4 7 8 9 0 2 3 5 6 4 6 0 7 1 3 5 2 8 9 3 5 1 6 7 8 0 9 4 2 Посмотрите на ортогональные соквадраты! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Рассмотрим двушку, принадлежащую классическим SODLS [DLK(2)] 0 3 4 6 7 2 9 8 5 1 2 1 7 9 5 3 8 6 0 4 8 6 2 5 0 9 1 3 4 7 1 5 6 3 9 7 4 0 2 8 9 8 3 2 4 6 5 1 7 0 6 7 1 0 8 5 2 4 9 3 4 9 0 7 3 8 6 5 1 2 3 4 9 8 2 1 0 7 6 5 7 2 5 4 1 0 3 9 8 6 5 0 8 1 6 4 7 2 3 9 [mate#1] 3 4 5 2 0 6 7 8 1 9 8 0 6 9 5 1 2 7 4 3 7 1 4 6 8 0 3 2 9 5 6 2 9 8 4 3 1 5 7 0 1 9 3 0 7 5 8 4 2 6 4 8 2 1 6 9 5 0 3 7 2 5 0 7 9 4 6 3 8 1 5 6 8 3 2 7 9 1 0 4 9 3 7 4 1 2 0 6 5 8 0 7 1 5 3 8 4 9 6 2 [mate#2] 4 5 6 7 0 8 3 9 2 1 9 7 8 1 6 2 0 3 5 4 3 2 5 8 9 7 4 0 1 6 8 0 1 9 5 4 2 6 3 7 2 1 4 0 3 6 9 5 7 8 5 9 0 2 8 1 6 7 4 3 0 6 7 3 1 5 8 4 9 2 6 8 9 4 7 3 1 2 0 5 1 4 3 5 2 0 7 8 6 9 7 3 2 6 4 9 5 1 8 0 Основной ДЛК двушки и ортогональный соквадрат mate#2 изоморфны со следующим изоморфизмом *T 0123456789 0123456789 4759318260 (изоморфизм первого вида по моей классификации). В приведённом формате (от программы Белышева) ортогональные соквадраты не являются узорчатыми ДЛК. А теперь от того же основного ДЛК нахожу ортогональные соквадраты программой Беляева 0 1 2 3 4 5 6 7 8 9 7 3 5 9 2 8 4 6 1 0 6 8 1 5 7 3 0 4 9 2 5 4 9 7 1 0 8 2 6 3 8 9 0 4 6 2 7 1 3 5 1 7 4 8 5 9 2 3 0 6 4 2 3 6 9 1 5 0 7 8 2 5 7 0 3 6 9 8 4 1 9 0 6 1 8 4 3 5 2 7 3 6 8 2 0 7 1 9 5 4 sq1 0 1 2 3 4 5 6 7 8 9 7 4 5 9 2 8 3 6 1 0 6 8 1 5 7 4 0 3 9 2 5 3 9 7 1 0 8 2 6 4 8 9 0 4 6 2 7 1 3 5 1 7 3 8 5 9 2 4 0 6 3 2 4 6 9 1 5 0 7 8 2 5 7 0 3 6 9 8 4 1 9 0 6 1 8 3 4 5 2 7 4 6 8 2 0 7 1 9 5 3 sq2 Square: 0 3 4 6 7 2 9 8 5 1 2 1 7 9 5 3 8 6 0 4 8 6 2 5 0 9 1 3 4 7 1 5 6 3 9 7 4 0 2 8 9 8 3 2 4 6 5 1 7 0 6 7 1 0 8 5 2 4 9 3 4 9 0 7 3 8 6 5 1 2 3 4 9 8 2 1 0 7 6 5 7 2 5 4 1 0 3 9 8 6 5 0 8 1 6 4 7 2 3 9 Посмотрите на ортогональные соквадраты sq1 и sq2, они узорчатые с кодом (3,4). Интересное замечание: программа Белышева производит такие ортогональные соквадраты, что self-orthogonal в классическом смысле пропадает и появляется self-orthogonal с изоморфизмом. Я преобразовала ортогональные соквадраты так, что self-orthogonal в классическом смысле стал очевиден (обозначения квадратов, как у Белышева) DLK(2) 0 3 4 6 7 2 9 8 5 1 2 1 7 9 5 3 8 6 0 4 8 6 2 5 0 9 1 3 4 7 1 5 6 3 9 7 4 0 2 8 9 8 3 2 4 6 5 1 7 0 6 7 1 0 8 5 2 4 9 3 4 9 0 7 3 8 6 5 1 2 3 4 9 8 2 1 0 7 6 5 7 2 5 4 1 0 3 9 8 6 5 0 8 1 6 4 7 2 3 9 mate#1 4 0 2 7 9 8 1 6 5 3 6 9 8 3 2 5 7 1 0 4 1 5 0 8 6 9 4 7 3 2 8 7 3 6 0 4 5 2 1 9 5 3 4 9 1 2 6 0 7 8 0 6 7 5 8 3 2 9 4 1 7 2 9 1 3 0 8 4 6 5 2 8 6 4 7 1 3 5 9 0 3 4 1 0 5 7 9 8 2 6 9 1 5 2 4 6 0 3 8 7 mate#2 0 2 8 1 9 6 4 3 7 5 3 1 6 5 8 7 9 4 2 0 4 7 2 6 3 1 0 9 5 8 6 9 5 3 2 0 7 8 4 1 7 5 0 9 4 8 3 2 1 6 2 3 9 7 6 5 8 1 0 4 9 8 1 4 5 2 6 0 3 7 8 6 3 0 1 4 5 7 9 2 5 0 4 2 7 9 1 6 8 3 1 4 7 8 0 3 2 5 6 9 И ещё один интересный момент: данная двушка производит при замыкании программой Белышева вторую двушку, которая тоже принадлежит классическим SODLS (а также однушку, тоже SODLS) 0 3 4 6 7 2 9 8 5 1 2 1 7 9 5 3 8 6 0 4 8 6 2 5 0 9 1 3 4 7 9 5 6 3 1 7 4 0 2 8 1 8 3 2 4 6 5 9 7 0 6 7 1 0 8 5 2 4 9 3 4 9 0 7 3 8 6 5 1 2 3 4 9 8 2 1 0 7 6 5 7 2 5 4 9 0 3 1 8 6 5 0 8 1 6 4 7 2 3 9 Сравните основные ДЛК этих двушек. Они узорчатые с кодом (1,9). При этом полное Замыкание даёт всего 3 КФ ОДЛК Найдено марьяжных КФ: count[1] = 1 count[2] = 2 Всего: 3 Найдено соквадратов: 5 КФ соквадратов: 3 Весьма интересные двушки, принадлежащие классическим SODLS. PS. Иллюстрации позже нарисую. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Проверила обе двушки утилитой Harry White GetType Monday 2020-03-02 12:40:27 ╠юёъютёъюх тЁхь (чшьр)
Order? 10
Enter the name of the squares file: input
.. writing type information to file inputTypeDetail_5.txt
Counts
------
2 diagonal Latin
2 natural \diagonal
2 self-orthogonal
Утилита не ошибается :) обе двушки self-orthogonal. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Сделала две иллюстрации. Это формат программы Беляева, здесь узорчатые ортогональные соквадраты, при этом они не изоморфны; изоморфны Square и sq2  Это мой формат (преобразовано из формата Белышева, чтобы хорошо видеть self-orthogonal)  |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
А теперь вторая двушка, порождаемая первой в замыкании  Здесь во втором формате (программа Белышева) ортогональки узорчатыми оказались. Сравните рисунок узора с первой двушкой, которая в первом формате изображена (программа Беляева)  Совершенно одинаковый рисунок узора, только циферки разные. Самое интересное: эти две двушки родственницы :) Каждая двушка в отдельности даёт 2 КФ ОДЛК. Казалось бы, вместе они должны дать 4 КФ. Ан нет! Вместе они дают только 2 КФ. Оказывается, mate #1 первой двушки изоморфен основному ДЛК второй двушки, а mate #1 второй двушки изоморфен основному ДЛК первой двушки. И уникальные только основные ДЛК двушек. Смотрим иллюстрацию  Я изобразила обе двушки так, чтобы было очевидно self-orthogonal. PS. Кажется, что-то подобное я читала в последних выступлениях Белышева на форуме boinc.ru, если правильно поняла. Тогда хороший пример для иллюстрации его теории. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну, недаром двушки эти родственницы, ведь вторая двушка порождается первой в замыкании. К этим двушкам родственницам надо добавить ещё и однушку родственницу, которая тоже порождается первой двушкой в замыкании. Однушка также принадлежит классическим SODLS и добавляет к этому семейству родственников одну КФ ОДЛК. Вот она, в моём формате  Таким образом, можно говорить о семействе конфигураций, полученных в замыкании. Все три конфигурации принадлежат классическим SODLS. Вместе все три конфигурации дают 3 КФ ОДЛК. Если бы это были не родственники и не SODLS, а полновесные двушки и однушка, то было бы 8 КФ ОДЛК. |

©2026 (C) Progger