Новый алгоритм постобработки
Message boards :
Science :
Новый алгоритм постобработки
Message board moderation
| Author | Message |
|---|---|
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Об алгоритмах вторичной обработки результатов (или постобработки) я уже писала. Таких алгоритмов мы имеем на сегодня несколько. У меня их уже штук семь. Самые известные и эффективные - это алгоритм Белышева Канонизатор ЛК по ДЛК и алгоритм поворота блоков. Я рассказывала уже об этих алгоритмах. Алгоритм Белышева в настоящее время заложен в его скрипт zamyk.bat, то есть выполняется на этапе первичной обработки сырых результатов BOINC-проектов. Это отличное решение! Алгоритм поворота блоков я постоянно использую для обработки ОДЛК, полученных в ручном проекте. Чем хороши алгоритмы вторичной обработки результатов? Они используют уже готовые решения, то есть минимум затрат. Берём известные решения и из них путём несложных преобразований получаем новые решения. Преобразования бывают разные. Ну, к примеру, всем хорошо известное: поворот блоков. Недавно я придумала ещё одно преобразование, очень простое. Но решения новые от ОДЛК получаются! Так например, обработка этим алгоритмом результатов с проекта Tomas Brada дала 496 новых ОДЛК. Это, конечно, совсем не лишние решения. А получаются они очень просто и быстро. О совсем новом алгоритме далее. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Очень мне нравятся узорчатые ДЛК, вот такие (узоры в ДЛК A и F раскрашены) 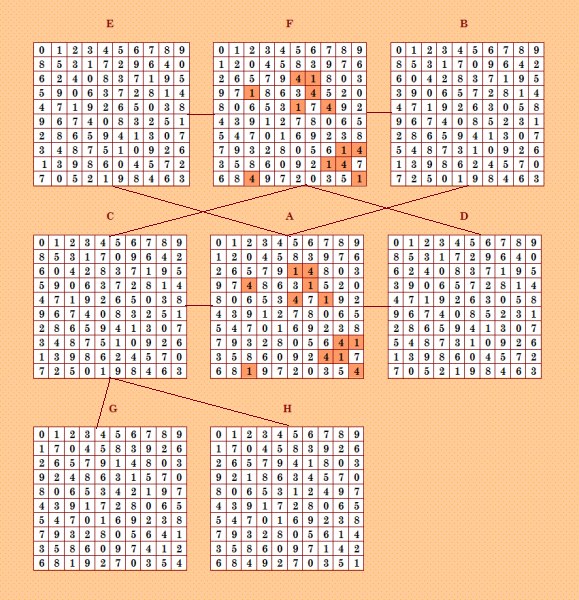 Смотрите тему об узорчатых ДЛК https://boinc.progger.info/odlk/forum_thread.php?id=80 Я пыталась реализовать поиск узорчатых ДЛК, написала две программы. Но пока этот поиск застрял у меня. Однако узорчатые ДЛК не дают мне покоя, постоянно сидят в голове. Мне кажется, что такие ДЛК будут давать интересные решения. Но заняться вплотную узорчатыми ДЛК всё никак не получается. Так вот, придумала алгоритм постобработки, который сам рисует узоры в ДЛК! Вчера получила несколько решений с узорчатыми ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Если вы внимательно посмотрите на квадраты A и F на иллюстрации, увидите, что узоры в них - это не просто поворот блоков. Это более сложные перестановки, которые не даёт простой поворот блоков в ДЛК. Поэтому такие ДЛК не находятся алгоритмом поворота блоков. Замечу, что такие сложные перестановки пытался делать коллега С. Беляев в своей программе lat05. Но он не довёл программу до ума. Пользоваться ей в настоящем виде весьма неудобно. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу ещё иллюстрацию с узорчатыми ДЛК 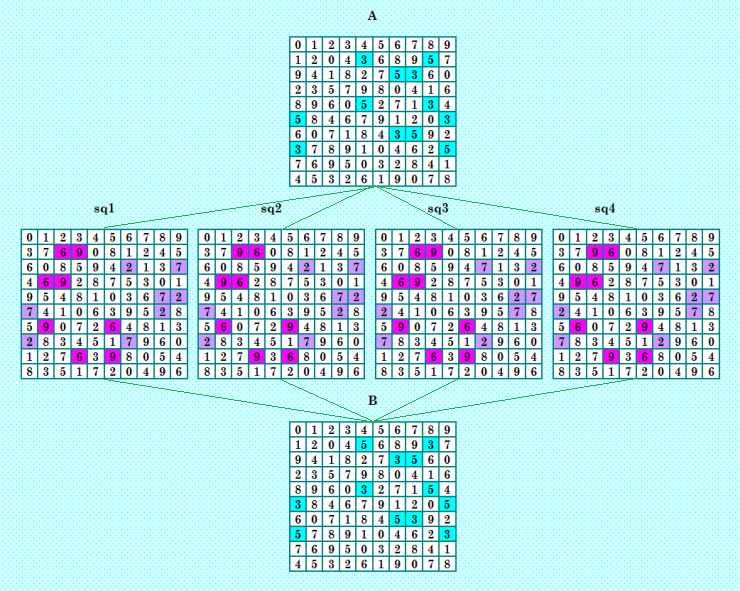 В ДЛК А и В вы видите поворот блоков, а в ДЛК sq1, sq2, sq3, sq4 более сложные перестановки. Далее покажу найденное вчера новым алгоритмом решение с узорчатыми ДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Итак, беру стандартную, ничем не примечательную однушку из существующей БД 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 8 9 6 5 3 9 8 0 5 1 4 2 7 6 6 4 9 7 2 3 5 8 1 0 5 8 1 6 9 0 7 3 4 2 8 0 5 2 1 6 9 4 3 7 9 5 7 8 0 4 3 6 2 1 2 7 4 5 6 8 0 1 9 3 4 3 6 1 7 9 2 0 5 8 7 6 3 9 8 2 1 5 0 4 Применяю к ней новый алгоритм и получаю новый ДЛК - узорчатый! Этот ДЛК даёт новую, оригинальную однушку. И это за одну минуту! Вот иллюстрация, сверху исходный ОДЛК 1, внизу новый ОДЛК 2  Узор раскрашен. Очевидно, что это не поворот блоков. Интересная перестановка! Столбики раскрашенные переставили. У меня программа выдала ещё решения; сейчас просмотрю их, если есть что интересное, покажу. Не отходя от существующей БД, можно получить сотни новых решений! Очень эффективный алгоритм. Главное - минимум затрат. Запустил где-нибудь в сторонке, и пусть себе ищет. PS. Недаром в детстве я очень любила игрушку калейдоскоп :) Большое спасибо изобретателям этой игрушки! |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Решения, которые получаются поворотом блоков, моя программа (новый алгоритм постобработки) тоже находит, разумеется. Пример беру стандартную однушку из имеющейся БД 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 7 8 9 5 6 3 8 5 1 9 6 7 4 2 0 6 4 0 7 2 3 1 8 9 5 5 7 9 6 8 0 3 1 4 2 8 5 1 9 3 4 2 0 6 7 4 0 7 2 6 8 9 5 3 1 9 3 8 0 1 2 5 6 7 4 2 6 4 5 7 9 0 3 1 8 7 9 6 8 5 1 4 2 0 3 Применяю к ней алгоритм, находится ОДЛК 2, полученный из исходного поворотом блоков. При этом полученный ОДЛК 2 даёт двушку. Иллюстрация 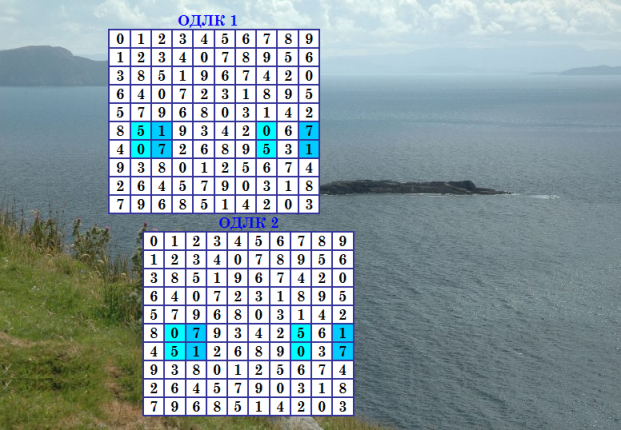 Важно отметить, что алгоритм ищет не просто узорчатые ДЛК, а именно ОДЛК. То есть на входе программы ОДЛК (берём их из имеющейся БД), на выходе программы новые ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Довольно много решений получено вчера программой постобработки результатов. Но... большинство решений с поворотом блоков у меня в БД уже имеется, так как я давно использую алгоритм поворота блоков. Более сложные перестановки дают оригинальные решения. Покажу интересное решение с поворотом блоков. Получила эти две однушки, пропускаю их через скрипт zamyk.bat и... получаю всего 2 КФ ОДЛК. Не сразу поняла, что однушечки получились изоморфные, то есть исходный ОДЛК 1 и полученный поворотом блоков ОДЛК 2 изоморфны.  Вот и такое случается. Не все повороты блоков дают новые решения. Этот факт давно известен, со времён исследования ЛК блочной структуры. PS. Такой изоморфизм для этих ДЛК выдаёт программа Белышева avtoizor_lk ** 4371098265 5628901734 8341265907 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Собираюсь модифицировать программу, чтобы узоров больше рисовала. Но программа длиннющая, надо всё заново переписывать для модификации, не скоро соберусь :) К тому же, ещё один алгоритм уже в разработке. Отвлекаться от него не хочется. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покажу ещё одно интересное решение, здесь исходный ОДЛК 1 даёт двушку, новый ОДЛК 2 тоже даёт двушку - оригинальную. Перестановка элементов - не поворот блоков. 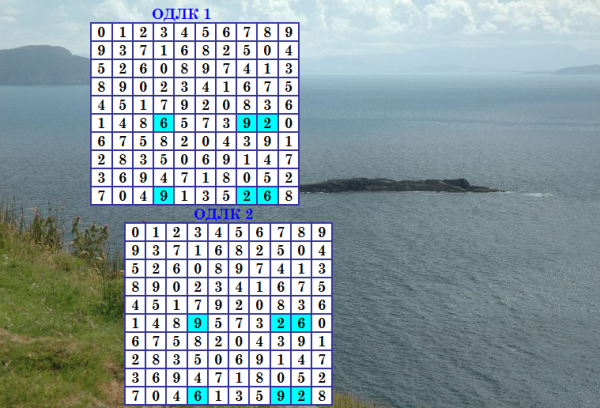 |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Берём все КФ ОДЛК в имеющейся БД и... смотрим на них. Может быть, кто-то обладает феноменальным даром делать все возможные перестановки элементов в уме :) Таким виртуозам флаг в руки! Переставляйте, господа! Ну, а я без программы не умею переставлять. Но программа у меня умная: она не просто переставляет элементы, а переставляет так, что получаются ОДЛК. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Понятно, что далеко не каждый ОДЛК даёт новый ОДЛК с помощью перестановок элементов. Покажу, как у меня сейчас программа работает . . . . . . . . . . POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 2 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 1 POSTROENO KVADRATOV 2 POSTROENO KVADRATOV 1 . . . . . . . Если написано "POSTROENO KVADRATOV 1", это программа возвращает исходный ОДЛК, новых ОДЛК не найдено. А когда написано "POSTROENO KVADRATOV 2", значит, найден новый ОДЛК, программа выдаёт исходный ОДЛК и новый ОДЛК. Во входном массиве сейчас только однушки. Программа уже достаточно протестирована, работает стабильно. Впереди модификация, о чём уже писала. После модификации программа будет находить больше новых ОДЛК. Как всем известно, программы я пишу на Бейсике. Если кто-то хочет посмотреть программу, поиграть с узорчатыми ДЛК, оптимизировать программу (с целью убыстрения), а также модифицировать (я скажу, как надо модифицировать), пишите мне. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Ну вот, покрутила немножко программу (обработано 500 известных ОДЛК из БД, однушек), нашла 9 новых, оригинальных ОДЛК; все они тоже дают однушки. Поворотов блоков здесь нет. Показаны парами: ОДЛК 1 и ОДЛК 2. 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 8 9 6 5 3 9 8 0 5 1 4 2 7 6 6 4 9 7 2 3 5 8 1 0 5 8 1 6 9 0 7 3 4 2 8 0 5 9 1 6 2 4 3 7 9 5 7 8 0 4 3 6 2 1 2 7 4 5 6 8 0 1 9 3 4 3 6 2 7 9 1 0 5 8 7 6 3 1 8 2 9 5 0 4 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 8 9 6 5 3 9 8 0 5 1 4 2 7 6 6 4 9 7 2 3 5 8 1 0 5 8 1 6 9 0 7 3 4 2 8 0 5 2 1 6 9 4 3 7 9 5 7 8 0 4 3 6 2 1 2 7 4 5 6 8 0 1 9 3 4 3 6 1 7 9 2 0 5 8 7 6 3 9 8 2 1 5 0 4 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 8 9 6 5 6 7 8 2 0 9 3 1 5 4 9 8 3 7 5 4 0 6 2 1 4 5 1 6 9 2 7 8 3 0 2 9 6 1 7 3 4 5 0 8 7 3 4 8 6 1 5 0 9 2 8 6 5 9 2 0 1 4 7 3 5 4 9 0 8 6 2 3 1 7 3 0 7 5 1 8 9 2 4 6 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 8 9 6 5 6 7 8 2 0 9 3 1 5 4 9 8 3 7 5 4 0 6 2 1 4 5 1 6 9 2 7 8 3 0 2 9 6 1 7 3 4 5 0 8 7 3 4 8 1 6 5 0 9 2 8 6 5 9 2 0 1 4 7 3 5 4 9 0 6 8 2 3 1 7 3 0 7 5 8 1 9 2 4 6 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 8 6 5 3 6 8 9 5 0 7 1 2 4 5 4 6 7 2 9 8 0 1 3 6 8 5 1 9 4 3 2 7 0 4 9 1 8 7 3 2 5 0 6 8 3 7 0 6 1 5 4 9 2 9 0 3 2 1 8 4 6 5 7 7 5 9 6 0 2 1 3 4 8 2 7 4 5 8 6 0 9 3 1 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 8 6 5 3 6 8 9 5 0 7 1 2 4 5 4 6 7 2 9 8 0 1 3 6 8 5 1 9 4 3 2 7 0 4 9 1 8 7 3 2 5 0 6 8 3 7 0 1 6 5 4 9 2 9 0 3 2 8 1 4 6 5 7 7 5 9 6 0 2 1 3 4 8 2 7 4 5 6 8 0 9 3 1 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 8 6 5 5 9 8 7 2 6 4 1 3 0 6 3 1 9 0 8 5 2 7 4 8 4 6 5 1 3 0 9 2 7 7 0 9 6 8 4 3 5 1 2 9 8 5 0 6 2 7 3 4 1 3 5 4 2 7 0 1 6 9 8 4 7 3 8 9 1 2 0 5 6 2 6 7 1 5 9 8 4 0 3 0 1 2 3 4 5 6 7 8 9 1 2 0 4 3 7 9 8 6 5 5 9 8 7 2 6 4 1 3 0 6 3 1 9 0 8 5 2 7 4 8 4 6 5 1 3 0 9 2 7 7 0 9 6 8 4 3 5 1 2 9 8 5 0 6 2 7 3 4 1 3 5 4 1 7 0 2 6 9 8 4 7 3 2 9 1 8 0 5 6 2 6 7 8 5 9 1 4 0 3 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 3 7 9 6 8 5 3 7 6 9 8 2 1 0 4 9 7 8 1 0 2 4 6 5 3 8 5 3 9 6 7 1 4 2 0 7 0 4 5 2 9 8 3 1 6 2 4 1 0 8 6 3 5 9 7 4 6 5 2 7 0 9 8 3 1 6 8 9 7 3 1 5 0 4 2 3 9 6 8 1 4 0 2 7 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 3 7 9 6 8 5 3 7 6 9 8 2 1 0 4 9 7 8 1 0 2 4 6 5 3 8 5 3 9 6 7 1 4 2 0 6 0 4 5 2 9 8 3 1 7 7 4 1 0 8 6 3 5 9 2 4 6 5 2 7 0 9 8 3 1 2 8 9 7 3 1 5 0 4 6 3 9 6 8 1 4 0 2 7 5 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 9 7 8 6 3 9 3 5 6 2 4 8 0 1 7 8 0 4 1 9 7 3 6 2 5 7 4 3 8 6 2 0 9 5 1 2 6 8 0 7 3 1 5 9 4 3 7 6 5 8 1 9 2 4 0 6 9 1 7 0 8 5 4 3 2 5 8 9 2 1 0 4 3 7 6 4 5 7 9 3 6 2 1 0 8 0 1 2 3 4 5 6 7 8 9 1 2 0 4 5 9 7 8 6 3 9 3 5 6 2 4 8 0 1 7 8 0 4 1 9 7 3 6 2 5 7 4 3 8 6 2 0 9 5 1 2 6 8 0 7 3 1 5 9 4 3 7 6 5 1 8 9 2 4 0 6 9 1 7 8 0 5 4 3 2 5 8 9 2 0 1 4 3 7 6 4 5 7 9 3 6 2 1 0 8 *** 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 7 8 9 5 3 8 5 4 7 3 9 2 6 1 0 4 7 1 8 9 3 0 5 2 6 2 9 5 0 7 4 3 8 6 1 9 3 7 5 2 6 1 4 0 8 3 6 8 1 5 2 9 0 4 7 6 4 3 9 8 0 5 1 7 2 5 8 9 6 0 1 7 2 3 4 7 0 6 2 1 8 4 3 9 5 0 1 2 3 4 5 6 7 8 9 1 2 0 4 6 7 8 9 5 3 8 5 4 7 3 9 2 6 1 0 4 7 1 8 9 3 0 5 2 6 2 9 5 0 7 4 3 8 6 1 9 3 7 5 2 6 1 4 0 8 3 6 8 1 5 2 9 0 4 7 6 4 3 9 0 8 5 1 7 2 5 8 9 6 1 0 7 2 3 4 7 0 6 2 8 1 4 3 9 5 *** 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 9 5 8 7 6 6 0 8 9 5 4 3 1 2 7 7 9 1 6 3 8 4 0 5 2 2 4 7 5 1 0 9 3 6 8 9 8 0 7 6 3 2 5 1 4 3 5 6 2 8 1 7 4 9 0 4 6 5 8 2 7 1 9 0 3 5 3 9 0 7 2 8 6 4 1 8 7 4 1 9 6 0 2 3 5 0 1 2 3 4 5 6 7 8 9 1 2 3 4 0 9 5 8 7 6 6 0 8 9 5 4 3 1 2 7 7 9 1 6 3 8 4 0 5 2 2 4 7 5 1 0 9 3 6 8 9 8 0 7 6 3 2 5 1 4 3 5 6 2 8 1 7 4 9 0 4 6 5 1 2 7 8 9 0 3 5 3 9 8 7 2 0 6 4 1 8 7 4 0 9 6 1 2 3 5 *** 0 1 2 3 4 5 6 7 8 9 1 2 8 4 9 7 3 5 6 0 7 4 5 6 8 1 9 0 2 3 6 5 1 9 3 2 7 4 0 8 8 0 7 5 6 4 1 9 3 2 4 9 0 8 5 3 2 1 7 6 3 7 6 1 0 8 4 2 9 5 9 6 3 7 2 0 5 8 4 1 5 8 9 2 7 6 0 3 1 4 2 3 4 0 1 9 8 6 5 7 0 1 2 3 4 5 6 7 8 9 1 2 8 4 9 7 3 5 6 0 7 4 5 6 8 1 9 0 2 3 6 5 1 9 3 2 7 4 0 8 8 0 7 5 6 4 1 9 3 2 4 9 0 2 5 3 8 1 7 6 3 7 6 1 0 8 4 2 9 5 9 6 3 7 2 0 5 8 4 1 5 8 9 0 7 6 2 3 1 4 2 3 4 8 1 9 0 6 5 7 Таким образом, получено 9 уникальных однушек, 18 уникальных КФ ОДЛК. Ещё раз подчеркну: для поиска данным алгоритмом ничего не надо генерировать. Исходные ДЛК для поиска готовы! Это известные ОДЛК из существующей БД. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Обалденное нашлось решение! Исходный ОДЛК 1 - основной ДЛК двушки, найденный ОДЛК 2 тоже даёт двушку, оригинальную. Посмотрите, какая сложная перестановка! Такую в уме сделать трудно.  Это уже настоящий узор, прямо как в калейдоскопе :) Эх, Белышева бы сюда! :) Он подвёл бы под все эти узоры теоретическую базу. Много ли узорчатых ДЛК? Да не просто ДЛК, а ОДЛК! Как найти их все? Да и Беляева не смогла уговорить выйти на форум. Что он там делает? Забросил, наверное, ЛК. Программу lat05 надо бы довести до ума, чтобы она хорошо строила сложные перестановки. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу кручу, а сама думаю над модификацией. Ой, тяжело :) Нарисовала картинку, всё разметила и расставила, теперь думаю... Программа длинная очень, но надо писать. Во-первых, в модифицированной программе хочу перейти ко второму формату, потому что все решения в BOINC-проектах (в трёх теперь!) получаются во втором формате. Ну и далее, есть во-вторых и в-третьих :) Модификация она на то и модификация. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу для второго формата пишу, примерно половина готова. А как выглядят узорчатые ДЛК во втором формате? Чтобы долго не искать, взяла их из свежей троечки, найденной в июне т. г. в проекте ODLK1 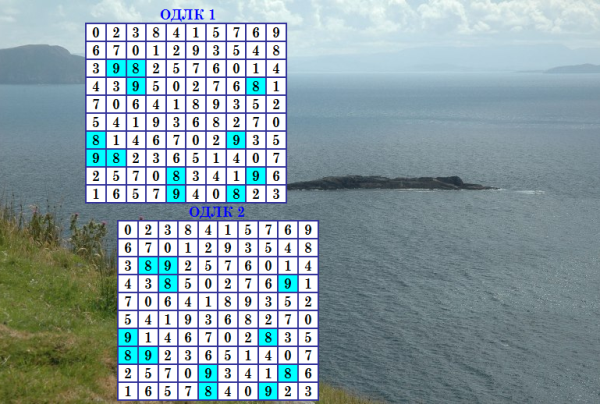 Очень симпатичный узор из восьмёрок и девяток. Это ортогональки троечки mate#1 и mate#2. Троечка вот [DLK(3)] 0 7 3 9 6 8 5 2 4 1 2 1 4 7 5 9 8 6 0 3 6 5 2 4 1 7 0 3 9 8 1 0 7 3 8 2 4 9 5 6 8 9 1 2 4 6 3 5 7 0 9 4 0 6 7 5 1 8 3 2 7 3 5 8 9 1 6 0 2 4 4 8 9 1 3 0 2 7 6 5 3 2 6 5 0 4 9 1 8 7 5 6 8 0 2 3 7 4 1 9 [mate#1] 0 2 3 8 4 1 5 7 6 9 6 7 0 1 2 9 3 5 4 8 3 9 8 2 5 7 6 0 1 4 4 3 9 5 0 2 7 6 8 1 7 0 6 4 1 8 9 3 5 2 5 4 1 9 3 6 8 2 7 0 8 1 4 6 7 0 2 9 3 5 9 8 2 3 6 5 1 4 0 7 2 5 7 0 8 3 4 1 9 6 1 6 5 7 9 4 0 8 2 3 [mate#2] 0 2 3 8 4 1 5 7 6 9 6 7 0 1 2 9 3 5 4 8 3 8 9 2 5 7 6 0 1 4 4 3 8 5 0 2 7 6 9 1 7 0 6 4 1 8 9 3 5 2 5 4 1 9 3 6 8 2 7 0 9 1 4 6 7 0 2 8 3 5 8 9 2 3 6 5 1 4 0 7 2 5 7 0 9 3 4 1 8 6 1 6 5 7 8 4 0 9 2 3 [mate#3] 0 2 3 8 4 1 5 7 6 9 6 8 0 1 2 9 3 5 4 7 3 7 9 2 5 8 6 0 1 4 4 3 7 5 0 2 8 6 9 1 8 0 6 4 1 7 9 3 5 2 5 4 1 9 3 6 7 2 8 0 9 1 4 6 7 0 2 8 3 5 7 9 2 3 6 5 1 4 0 8 2 5 8 0 9 3 4 1 7 6 1 6 5 7 8 4 0 9 2 3 mate#3 тоже узорчатый. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Вот нашла ещё иллюстрацию для узорчатых ДЛК во втором формате; смотрите на иллюстрации ОДЛК A и B. Симпатичный узор из нулей и единиц. Кстати, узорчатые ОДЛК A и B дают одну и ту же четвёрку ортогональных ДЛК. Четвёрки-близняшки. 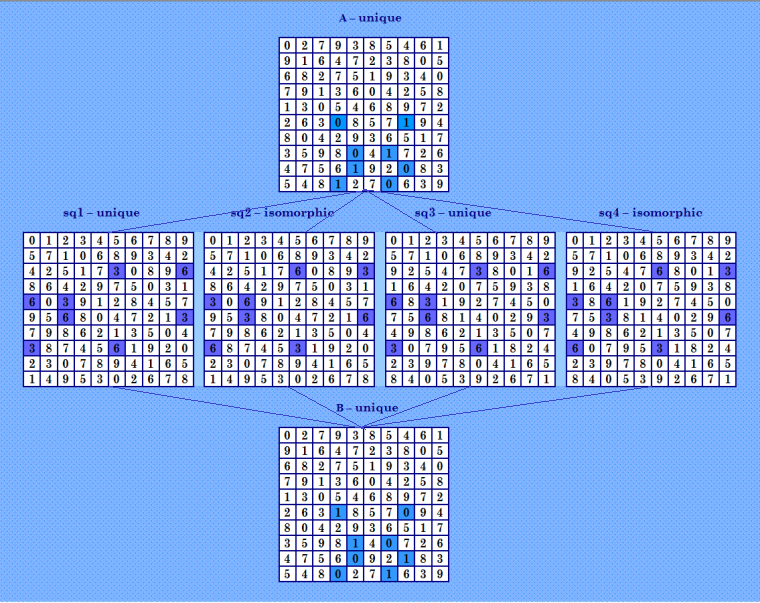 Ортогональки четвёрок тоже узорчатые, но они в формате 1. Важно отметить, что не только повороты блоков, но и более сложные перестановки элементов могут давать изоморфные ДЛК. Смотрите на ДЛК sq1 и sq2, sq3 и sq4. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Программу для второго формата написала - для нахождения узорчатых ОДЛК. Сейчас тестирую, ввела 320 основных ДЛК однушек (конечно, в формате 2). Посмотрю, что интересного найдётся. Ну, какие-то решения есть (видно на экране); насколько они интересные, пока не знаю. Жду окончания работы программы. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Решений найдено более десятка, но все не интересные. Какая-то скучная порция однушек попалась: во всех основных ДЛК выполнен только поворот блоков, причём такой, что преобразованный ДЛК изоморфен исходному. Вот примеры 0 4 3 7 8 2 9 6 5 1 6 1 9 5 7 4 3 8 0 2 9 5 2 1 6 8 7 3 4 0 2 0 8 3 5 7 4 1 9 6 5 2 1 0 4 6 8 9 7 3 8 3 7 9 2 5 1 0 6 4 1 7 0 8 9 3 6 4 2 5 4 6 5 2 3 9 0 7 1 8 3 9 6 4 1 0 2 5 8 7 7 8 4 6 0 1 5 2 3 9 0 4 3 7 8 2 9 6 5 1 6 1 9 5 7 4 3 8 0 2 9 5 2 1 6 8 7 3 4 0 2 0 8 3 5 7 4 1 9 6 5 2 1 0 4 6 8 9 7 3 8 3 7 9 2 5 1 0 6 4 1 7 0 8 3 9 6 4 2 5 4 6 5 2 9 3 0 7 1 8 3 9 6 4 0 1 2 5 8 7 7 8 4 6 1 0 5 2 3 9 *** 0 5 7 9 6 8 4 2 3 1 9 1 6 2 8 7 3 5 0 4 1 6 2 7 9 4 8 3 5 0 7 0 1 3 5 9 2 6 4 8 8 7 3 5 4 6 0 1 9 2 2 3 8 0 7 5 9 4 1 6 4 9 5 8 2 1 6 0 7 3 6 8 9 4 0 3 1 7 2 5 3 4 0 6 1 2 5 9 8 7 5 2 4 1 3 0 7 8 6 9 0 5 7 9 6 8 4 2 3 1 9 1 6 2 8 7 3 5 0 4 1 6 2 7 9 4 8 3 5 0 7 0 1 3 5 9 2 6 4 8 8 7 3 5 4 6 0 1 9 2 2 3 8 0 7 5 9 4 1 6 4 9 5 8 1 2 6 0 7 3 6 8 9 4 3 0 1 7 2 5 3 4 0 6 2 1 5 9 8 7 5 2 4 1 0 3 7 8 6 9 Решения показаны парами: ОДЛК 1, ОДЛК 2. Но программа работает стабильно. Это уже хорошо, можно запускать порцию побольше и искать новые решения. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Покрутила ещё немножко программу для ДЛК формата 2. Модифицированная программа работает чуть быстрее, соответственно больше ДЛК обрабатывается в единицу времени, повеселее стало :) Решения стабильно находятся, есть даже и уникальные. Покажу два свежих примера; в этих ДЛК узоры получены не поворотом блоков, Преобразованные ДЛК дают оригинальные однушки.  Между прочим, эти ДЛК из линейки 15, то бишь псевдоассоциативные. А вот какое интересное пятнышко, родинка на ОДЛК :)  Завтра покручу ещё, если найдётся что-то интересное, покажу. Но главный интерес достигнут - новые решения получаются вторичной обработкой известных решений! И довольно много. |
 Natalia Makarova Natalia MakarovaSend message Joined: 6 Apr 17 Posts: 16992 Credit: 0 RAC: 0 |
Решила проверить, как с преемственностью узорчатости у ДЛК форматов 1 и 2. Вот это обалденное решение Обалденное нашлось решение! проверила в формате 2  Всё замечательно! Узорчатые ОДЛК получены. Они уникальные и каждый даёт двушку [DLK(2)] 0 2 7 4 9 8 3 5 6 1 3 1 8 9 6 7 5 2 0 4 9 6 2 5 1 0 7 3 4 8 8 0 5 3 2 9 4 6 1 7 7 3 1 8 4 6 9 0 2 5 6 9 0 1 8 5 2 4 7 3 1 5 3 2 7 4 6 8 9 0 4 8 9 6 3 1 0 7 5 2 2 7 4 0 5 3 1 9 8 6 5 4 6 7 0 2 8 1 3 9 [mate#1] 0 5 4 8 2 1 9 6 7 3 8 1 3 7 6 0 5 2 4 9 4 9 8 3 0 6 2 1 5 7 9 2 0 5 1 3 7 4 6 8 5 7 2 6 4 8 0 3 9 1 1 8 7 4 5 9 6 0 3 2 7 4 6 0 9 2 3 8 1 5 6 0 9 2 3 5 1 7 8 4 3 6 1 9 7 4 8 5 2 0 2 3 5 1 8 7 4 9 0 6 [mate#2] 0 5 4 8 2 1 9 6 7 3 8 1 3 7 6 0 5 2 4 9 4 8 9 3 0 6 2 1 5 7 9 2 0 5 1 3 7 4 6 8 5 7 2 6 4 9 0 3 8 1 1 9 7 4 5 8 6 0 3 2 7 4 6 0 9 2 3 8 1 5 6 0 8 2 3 5 1 7 9 4 3 6 1 9 7 4 8 5 2 0 2 3 5 1 8 7 4 9 0 6 [DLK(2)] 0 2 7 4 9 8 3 5 6 1 3 1 8 9 6 7 5 2 0 4 9 6 2 5 1 0 7 3 4 8 8 0 5 3 2 9 4 6 1 7 7 3 1 8 4 6 9 0 2 5 1 9 3 6 8 5 0 4 7 2 4 5 0 2 7 1 6 8 9 3 6 8 9 1 3 4 2 7 5 0 2 7 4 0 5 3 1 9 8 6 5 4 6 7 0 2 8 1 3 9 [mate#1] 1 4 3 0 2 7 5 6 8 9 0 7 9 8 6 1 4 2 3 5 3 0 5 9 1 6 2 7 4 8 5 2 1 4 7 9 8 3 6 0 4 8 2 6 3 5 1 9 0 7 8 5 6 2 4 0 7 1 9 3 6 3 8 1 5 4 9 0 7 2 7 1 0 3 9 2 6 8 5 4 9 6 7 5 8 3 0 4 2 1 2 9 4 7 0 8 3 5 1 6 [mate#2] 3 1 4 5 6 7 0 8 9 2 5 7 2 9 8 3 1 6 4 0 4 0 5 2 3 8 6 7 1 9 0 6 3 1 7 2 9 4 8 5 1 9 6 8 4 5 3 2 0 7 9 5 8 6 1 0 7 3 2 4 8 4 9 3 0 1 2 5 7 6 7 3 0 4 2 6 8 9 5 1 2 8 7 0 9 4 5 1 6 3 6 2 1 7 5 9 4 0 3 8 Таким образом, преемственность узорчатости в ДЛК форматов 1 и 2 имеет место. |

©2026 (C) Progger