Поясню, почему показанный в предыдущем посте псевдоассоциативный ДЛК надо запомнить.

Главная стратегия поиска эффективных алгоритмов - ищите красивые структуры.
Красивые структуры уже дали нам несколько эффективных алгоритмов, например:

1. Семейства ЛК блочной структуры;
2. Симметричные по Гергели-Брауну ДЛК;
3. Симметрии серии (х,31,31) по Белышеву;
4. Псевдоассоциативные ДЛК.

Показанный в предыдущем посте псевдоассоциативный ДЛК получен генератором 5 в линейке №15.
Он имеет красивую структуру: помимо того, что он псевдоассоциативный, в нём ещё нарушения ассоциативности не хаотичны, а образуют горизонтальную симметрию. Таким образом, в этом ДЛК получается смешанная симметрия.
У этого ДЛК довольно высокая степень ассоциативности - 0,8.
А много ли псевдоассоциативных ДЛК такой структуры найдёт генератор 5 в линейке №15?
Хороший вопрос!
Понятно, что не для любой первой строки в СН ДЛК линейки №15 ДЛК такой структуры возможны.
Вчера написала программку фильтрации строк, она выдала 1424 строки из 6164 строк в линейке №15.
Строка

0 7 5 8 6 9 2 4 3 1

для которой получен показанный ДЛК, разумеется, в списке.
Крупно повезло!
Если бы я взяла для тестирования строку, которой нет в списке, не вышла бы на такой изумительный псевдоассоциативный ДЛК.

А теперь надо в ветви PADLS, генератор 5, rule 15 выделить маленькую веточку: смешанная симметрия по образцу показанного ДЛК.
Для этого надо написать новый генератор, который будет генерировать только ДЛК такой структуры.
Очевидно, что если выполнить полностью ветвь PADLS, генератор 5, rule 15, то незачем выделять маленькую веточку.
Но ветвь PADLS, генератор 5, rule 15 очень большая, я вот никак один WU не обработаю - несколько миллионов псевдоассоциативных ДЛК.
А веточка "смешанная симметрия" будет намного меньше.

Программа-генератор для веточки "смешанная симметрия" почти написана, осталось чуть-чуть.
И покажу ДЛК со смешанной симметрией из линейки №15.
Степень ассоциативности всех этих ДЛК равна 0,8. Достаточно высокая.
Много ли будет генерироваться таких ДЛК? Скоро узнаем.

Первый псевдоассоциативный ДЛК (с нарушением ассоциативности по горизонтальной симметрии) в линейке №15 получен!
Для теста взяла ту же самую первую строку, с которой ДЛК данной структуры был обнаружен

0 7 5 8 6 9 2 4 3 1 

Встречайте квадратик, он очень красивый



Показан ДЛК и его КФ.
Интересно: при переходе к КФ структура ДЛК сохранилась.

Массовую генерацию ещё не делала. Сейчас попробую для этой же строки.
Ну очень интересно: много ли будет ДЛК такой структуры в одном WU?

Программа сообщила

. . . . . . . . 
 0  7  5  8  6  9  2  4  3  1 
 7  1  9  2  5  6  3  8  0  4 
 5  4  2  0  8  7  9  3  1  6 
 6  5  8  3  1  0  4  2  9  7 
 9  3  0  1  4  2  5  6  7  8 
 1  2  3  4  7  5  8  9  6  0 
 3  0  7  5  9  8  6  1  4  2 
 4  8  6  9  2  1  0  7  5  3 
 2  9  1  6  3  4  7  0  8  5 
 8  6  4  7  0  3  1  5  2  9 
 0  7  5  8  6  9  2  4  3  1 
 7  1  9  2  5  6  3  8  0  4 
 5  4  2  9  8  7  0  3  1  6 
 6  5  8  3  1  0  4  2  9  7 
 9  3  0  1  4  2  5  6  7  8 
 1  2  3  4  7  5  8  9  6  0 
 3  0  7  5  9  8  6  1  4  2 
 4  8  6  0  2  1  9  7  5  3 
 2  9  1  6  3  4  7  0  8  5 
 8  6  4  7  0  3  1  5  2  9 
GENERATED SQUARES 192 

Да, ожидаемый результат. Структура очень жёсткая, квадратики такие на вес золота :)

Надеюсь, что не ошиблась в программе (писала очень быстро); но генерирует ДЛК. Подводные камни могут позже всплыть.
Ну вот, можно приступать к проверке этой веточки эксперимента. Всего 1424 WUs, и ДЛК в одном WU совсем мало.

PS. Проверила Канонизатором, сгенерированные ДЛК дали 192 КФ, все уникальные, значит, квадратики.
Сейчас обработаю их программой family_mar.
От этой порции марьяжных ДЛК не найдено.

В настоящее время в работе находятся следующие ветви эксперимента PADLS
1. PADLS rule 51 (выполняет XAVER);
2. PADLS rule 39 (выполняет Demis);
3. PADLS, генератор 4, rule 38 (выполняю я);
4. PADLS TOTAL rule 51 (выполняется в BOINC-проекте Tomas Brada).

Понятно, что ветвь 1 входит в ветвь 4.
Но прекращать ветвь эксперимента PADLS rule 51 не будем; по крайней мере, пока идут уникальные решения. Ветвь выполняется давно и успешно.

Эти ветви готовы к выполнению
1. PADLS rule 16;
2. PADLS, генератор 4, rule 15;
3. PADLS, генератор 5, rule 15;
4. PADLS TOTAL rule 15;
5. PADLS TOTAL rule 38.

Понятно, что ветви 2 и 3 входят в ветвь 4.
А также ветвь 3 из выполняемых ветвей входит в ветвь 5 последнего списка.

Цитата

Идеи у меня не закончились. Есть ещё как минимум две.
Вот закончу с тестированием одного WU в экспериментах PADLS, генератор 5, rule 15 и PADLS rule 16, тогда попробую реализовать новые идеи.

Одну идею уже опробовала.
Встречайте псевдоассоциативный ДЛК из линейки №38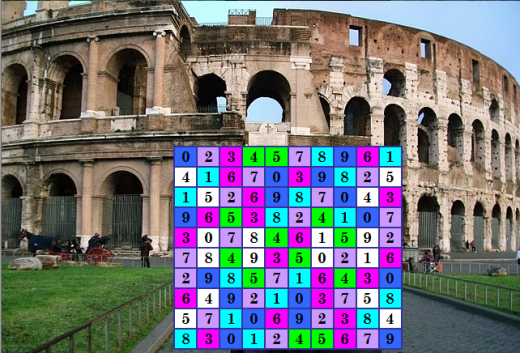



Этот ДЛК получен новым генератором, аналогичным генератору в ветви эксперимента PADLS rule 39.
Степень ассоциативности ДЛК равна 0,84, довольно высокая.
Для линейки №38 это будет генератор 5.
В настоящее время у меня выполняется ветвь PADLS, генератор 4, rule 38. К этой ветви добавилась ветвь PADLS, генератор 5, rule 38.

Тестирование одного WU выполнила, правда, не полностью. Сгенерировала маленькую порцию 300000 псевдоассоциативных ДЛК, они дали 242914 КФ.
Проверила; нашлось 7 марьяжных ДЛК, они дали в Замыкании 15 КФ ОДЛК (есть одна двушка), уникальных 8 КФ ОДЛК.
Показанный ДЛК - последний ДЛК в этой порции.
Хорошая ветвь!
В этой ветви 3440 WUs. К сожалению, строки для двух генераторов (4 и 5) в линейке №38 не совпадают.
Для генератора 4 имеем 6200 WUs.
Поэтому работу двух генераторов в линейке можно объединить только для совпадающих строк, которых 3440.

PS. Посмотрите внимательно на показанный ДЛК.
Нарушения ассоциативности (в белых ячейках) происходят по вертикальной симметрии.
Опять смешанная симметрия!
Чудесный квадратик!