Posts by Natalia Makarova

1) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14184) Posted 15 minutes ago by Natalia Makarova Post: Продолжаю с квадратиками на раскраске разбираться. Смотрите сообщение https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=14179 Во второй строке моего фрагмента находятся элементы: 128, 129, 130, …, 143. Вот их valids 128, 3 129, 4 130, 4 131, 5 132, 4 133, 5 134, 5 135, 6 136, 4 137, 5 138, 5 139, 6 140, 5 141, 6 142, 6 143, 7 Здесь тоже не получается с элементами, у которых valids=6. Элементу 143 с valids=7 соответствует фиолетовый квадратик. gris, вы не напутали с valids=6? Почему элементы с valids=6 у вас зелёные? А также элементы с valids=3 зелёные.
2) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14183) Posted 30 minutes ago by Natalia Makarova Post: У черепашки ещё интересная находка 1431966425765269: [0, 18, 30, 60, 78, 84, 108, 118, 130, 144, 150, 168, 190, 210, 228] 1431966425765269: [0, 0, 0, 0, 0, 0, 0, 4, 10, 0, 0, 0, -8, 0, 0] 1431966425765269: [1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1] valids=12 ncode=8093 Код в самой верхней части спектра. И ещё 1483793250263003: [0, 18, 30, 60, 78, 84, 86, 114, 138, 144, 164, 170, 180, 210, 228] 1483793250263003: [0, 0, 0, 0, 0, 0, -22, 0, 18, 0, 14, 2, -18, 0, 0] 1483793250263003: [1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 1] valids=10 ncode=8017
3) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14182) Posted 2 hours ago by Natalia Makarova Post: С двумя "дырками" найдено-таки приближение к центральной 15-ке! 977422707649613: [0, 18, 30, 60, 78, 84, 96, 114, 120, 144, 150, 176, 198, 210, 228] 977422707649613: [0, 0, 0, 0, 0, 0, -12, 0, 0, 0, 0, 8, 0, 0, 0] 977422707649613: [1, 1, 1, 1, 1, 1, 0, 1, 1, 1, 1, 0, 1, 1, 1] valids=13 ncode=8059 Ура, товарищи! Осталось две "дырки" убить :)
4) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14181) Posted 2 hours ago by Natalia Makarova Post: gris писал в сообщении https://dxdy.ru/post1636865.html#p1636865 Ничего, что я невтему Посмотрел, что там с центральными подпаттернами 19-252. Интересно с 9-108. Нашёл все приближения с прибитыми краями. Коды тем же способом в pt[2..8]. Их 128 штук, valids изменяется от 2 до 9. Спектр: [0 2 5531; 34 4 5903; 2 3 7349; ... 119 8 445455169; 95 8 623911909; 127 9 909894593] (code, valids, первое появление) Интересно, что последний код появляется последним и с большим отрывом. Почему же "невтему"? :) Очень даже в тему! Вы же как раз про это тему и начинали. Да, вот с этого и надо было начинать! А то размечтались - заполнить спектр для 19-252 на 99% :)) Вот спектр для 9-108 заполнили на 100%, замечательно! Теперь заполните на 100% спектр для центральных 11-ок. Найдите несколько миллионов кортежей 9-108. Нашли? И матрёшечные имеются? Очень хорошо. Теперь найдите несколько миллионов кортежей 11-168. Нашли? И матрёшечные есть? Отлично! Теперь найдите несколько миллионов кортежей 13-192. Не нашли? Плохо! Вот когда найдёте несколько миллионов кортежей 13-192 и проанализируете их, тогда можно искать кортежи 15-228. Ну, искать можно все сразу, если ресурсы позволяют. Банально? А как иначе? Ну, вот начал г. Петухов сразу с поиска кортежа 19-252. Год ищет и... не находит! К тому же, утверждает, что кортежи 19-252 находятся быстрее, чем кортежи 17-240. Только вот кортежи 17-240 у него нашлись-таки, в количестве двух штук. А кортежа 19-252 нет как нет! Так что, как ни банальна изложенная стратегия, а очень древняя - от простого к сложному. Итак, полный спектр приближений к центральной 11-ке в студию! :) Я пытаюсь спектр приближений к центральной 15-ке заполнить. Одновременно ищу их (центральные 15-ки).
5) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14180) Posted 3 hours ago by Natalia Makarova Post: Ядряра Ну так а вы тему-то читаете? vicvolf Нет. Это не очень интересно. Может быть только с точки зрения вычислений и тема явно должна быть в другом разделе. Общих математических вопросов здесь точно нет. https://dxdy.ru/post1636876.html#p1636876 Хи-хи-хи! Ну, очень смешно. И что это прикололись (уже двое), что тема не в том разделе? Ну, не интересная тема, так и гуляйте лесом, собирайте грибы да ягодки. Чего лезть в тему с глупыми банальностями, да ещё с менторским тоном. При чём тут вообще раздел? От изменения раздела тема не станет менее интересной или более интересной. Модератор решил оставить тему в этом разделе. Нет же, неймётся vicvolf. Когда по теме нечего сказать, начинают всякую фигню говорить про раздел, про Вавилонскую башню и т.д. А по теме vicvolf явно сказать нечего, как он ни пыжится. PS. vicvolf, похоже, про запятые вообще не знает :))) Может быть только с точки зрения вычислений и тема явно должна быть в другом разделе. Или у него клавиша с запятой выбита. Жаль, что в Правилах форума dxdy.ru не предусмотрено наказание за умышленное нарушение орфографии и пунктуации. Ведь нечитабельные же тексты с такой пунктуацией, как у vicvolf и у Ядряры, да и у его лучшего друга г. Петухова. Вот фраза г. Петухова Возможно рассказать мне про формулы чтобы я их встроил в свою прогу будет быстрее чем Вам разбираться в моей, Красиво, не правда ли? Это по правилам для пирожков и порошков написано? :)
6) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14179) Posted 3 hours ago by Natalia Makarova Post: 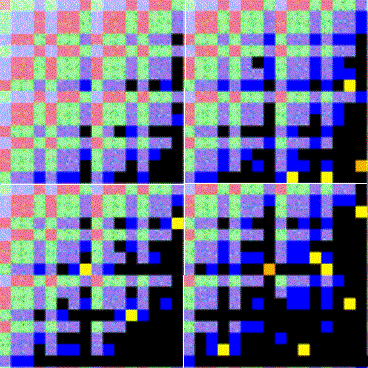Я вот в Ворде нарисовала левый верхний подквадрат 16х16 :) Старалась придерживаться раскраски оригинала, только у меня чёрные квадратики заменены белыми. Ну, могла что-то напутать, так как визуально переносила раскраску. Если я правильно понимаю, все раскрашенные квадратики соответствуют найденным элементам спектра, а белые квадратики - не найденным. В первой строке квадрата 16х16, показанного на моём фрагменте, находятся элементы: 0, 1, 2, ..., 15. code=0, valids=2 Далее (первый столбец - code, второй столбец - valids) 1, 3 2, 3 3, 4 4, 3 5, 4 6, 4 7, 5 8, 3 9, 4 10, 4 11, 5 12, 4 13, 5 14, 5 15, 6 Итак: зелёные квадратики - valids=3 сиреневые квадратики - valids=4 оранжевые квадратики - valids=5 Ой, что-то квадратик с кодом 15 не получился :( Он зелёный, а у него же valids равен не 3, а 6. Где у меня ошибка?
7) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14178) Posted 3 hours ago by Natalia Makarova Post: У черепашки два симпатичных приближения подряд нашлись 1115917772971549: [0, 18, 30, 60, 78, 84, 114, 118, 120, 130, 148, 184, 198, 214, 228] 1156387351524799: [0, 0, 0, 0, 0, 0, 0, 6, 12, 0, -2, 0, -26, -12, 0] 1156387351524799: [1, 1, 1, 1, 1, 1, 1, 0, 0, 1, 0, 1, 0, 0, 1] valids=10 ncode=8084 1112141616190999: [0, 18, 30, 60, 78, 84, 88, 114, 120, 130, 132, 168, 202, 210, 228] 1112141616190999: [0, 0, 0, 0, 0, 0, -20, 0, 0, -14, -18, 0, 4, 0, 0] 1112141616190999: [1, 1, 1, 1, 1, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1] valids=11 ncode=8037 Коды в самой верхней части спектра; конечно, уникальные.
8) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14177) Posted 4 hours ago by Natalia Makarova Post: Новая порция Norm-чисел дала следующие приближения к ключевой 17-ке с valids>9 (04:10) gp > \rraznost.txt logfile = "raznost_res.txt" 31166313265008084439947043: [0, 6, 28, 66, 70, 84, 90, 114, 118, 126, 148, 150, 174, 198, 216, 234, 240] 31166313265008084439947043: [0, 0, 4, 30, 4, 0, 0, 0, -2, 0, -2, -6, 0, -6, 0, 0, 0] valids=10 code=18251 29160708363878191325921783: [0, 6, 26, 36, 44, 98, 110, 114, 120, 126, 150, 168, 174, 180, 204, 234, 240] 29160708363878191325921783: [0, 0, 2, 0, -22, 14, 20, 0, 0, 0, 0, 12, 0, -24, -12, 0, 0] valids=10 code=20969 29160708363941044710984097: [0, 6, 10, 16, 24, 84, 90, 114, 124, 126, 136, 156, 174, 190, 196, 234, 240] 29160708363941044710984097: [0, 0, -14, -20, -42, 0, 0, 0, 4, 0, -14, 0, 0, -14, -20, 0, 0] valids=10 code=18265 31166313265209928893791923: [0, 6, 24, 36, 58, 60, 76, 84, 90, 126, 150, 156, 198, 204, 216, 238, 240] 31166313265209928893791923: [0, 0, 0, 0, -8, -24, -14, -30, -30, 0, 0, 0, 24, 0, 0, 4, 0] valids=10 code=28790 29160708364247429648318027: [0, 12, 44, 56, 66, 84, 90, 114, 120, 126, 146, 170, 176, 194, 216, 234, 240] 29160708364247429648318027: [0, 6, 20, 20, 0, 0, 0, 0, 0, 0, -4, 14, 2, -10, 0, 0, 0] valids=10 code=4035 29160708363382301452898693: [0, 6, 20, 24, 26, 36, 90, 104, 120, 126, 150, 170, 174, 204, 216, 230, 240] 29160708363382301452898693: [0, 0, -4, -12, -40, -48, 0, -10, 0, 0, 0, 14, 0, 0, 0, -4, 0] valids=10 code=17134 Все коды не уникальные. Но я всё равно добавляю эти приближения в спектр, вот так 17134 (33565634429687, 29160708363382301452898693) Вторые приближения могут пригодиться для исследования. Расстояние между двумя приближениями впечатляет. Интересно: в трёх из этих приближений содержатся приближения к центральной 15-ке. Вот они 31166313265008084439947049: 6, 28, 66, 70, 84, 90, 114, 118, 126, 148, 150, 174, 198, 216, 234 29160708363878191325921789: 6, 26, 36, 44, 98, 110, 114, 120, 126, 150, 168, 174, 180, 204, 234 29160708363941044710984103: 6, 10, 16, 24, 84, 90, 114, 124, 126, 136, 156, 174, 190, 196, 234 (паттерны не нормализованы). Сейчас я их своей утилитой проверю. Вот 31166313265008084439947049: [0, 22, 60, 64, 78, 84, 108, 112, 120, 142, 144, 168, 192, 210, 228] 31166313265008084439947049: [0, 4, 30, 4, 0, 0, 0, -2, 0, -2, -6, 0, -6, 0, 0] valids=8 code=933 29160708363878191325921789: [0, 20, 30, 38, 92, 104, 108, 114, 120, 144, 162, 168, 174, 198, 228] 29160708363878191325921789: [0, 2, 0, -22, 14, 20, 0, 0, 0, 0, 12, 0, -24, -12, 0] valids=8 code=2292 29160708363941044710984103: [0, 4, 10, 18, 78, 84, 108, 118, 120, 130, 150, 168, 184, 190, 228] 29160708363941044710984103: [0, -14, -20, -42, 0, 0, 0, 4, 0, -14, 0, 0, -14, -20, 0] valids=8 code=940 Коды не уникальные.
9) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14176) Posted 4 hours ago by Natalia Makarova Post: Ахиллес подключился в диапазоне больших чисел (00:52) gp > \r 15unik.txt logfile = "15unik_res.txt" 49450000 from number 49452000 to number [0,18,30,60,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 9917716236928500000 - 9918117558469250130 2293760 formulae expected 9917881770622750303: [0, 18, 30, 58, 78, 84, 108, 124, 130, 144, 178, 184, 198, 210, 228] 9917881770622750303: [0, 0, 0, -2, 0, 0, 0, 10, 10, 0, 28, 16, 0, 0, 0] 9917881770622750303: [1, 1, 1, 0, 1, 1, 1, 0, 0, 1, 0, 0, 1, 1, 1] valids=10 ncode=7059 . . . . . . . . . С ходу симпатичное приближение найдено с кодом в верхней части спектра. Проверка начинается с интервала search in 9917716236928500000 - 9918117558469250130 Задано 2000 периодов 31#. Таким образом, все трое у меня ищут приближения к центральной 15-ке :) По одному потоку у каждого. Черепашка работает в диапазоне малых чисел, Ахиллесы - в диапазоне больших чисел. Нам осталось найти 2208 элементов спектра приближений к центральной 15-ке (из 8192). Это, конечно, много, но бОльшая часть найдена.
10) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14175) Posted 12 hours ago by Natalia Makarova Post: А это Ахиллес-3 работает в диапазоне больших чисел ? \r 15unik.txt logfile = "15unik_res.txt" 49430919 from number 49432919 to В number [0,18,30,60,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 9913889342216329470 - 9914290663757079600 2293760 formulae expected 9914285507998325833: [0, 18, 30, 58, 78, 96, 108, 114, 124, 136, 150, 184, 198, 210, 228] 9914285507998325833: [0, 0, 0, -2, 0, 12, 0, 0, 4, -8, 0, 16, 0, 0, 0] 9914285507998325833: [1, 1, 1, 0, 1, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1] valids=10 ncode=6859 9914111937804839143: [0, 10, 30, 60, 78, 84, 108, 114, 130, 144, 166, 184, 186, 210, 228] 9914111937804839143: [0, -8, 0, 0, 0, 0, 0, 0, 10, 0, 16, 16, -12, 0, 0] 9914111937804839143: [1, 0, 1, 1, 1, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1] valids=10 ncode=4049 Здесь глухо, два решения выдано и - тишина! Зато в этом диапазоне может быть найдена полная центральная 15-ка. Между этими двумя центральными 15-ми 3665619319531504883, 1006882292528806742273. Первая не матрёшечная, вторая матрёшечная. Ну, матрёшечная вряд ли найдётся, хотя как знать - вдруг Врублевский не нашёл минимальную ключевую 17-ку.
11) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14174) Posted 13 hours ago by Natalia Makarova Post: Сформировала новый массив пропущенных элементов для спектра приближений к центральной 15-ке. Добавлено в спектр 353 уникальных элемента. Массив пропущенных элементов содержит 2208 элементов. Всего найдено на данный момент 5984 уникальных элемента, 73,05%. Черепашка работает в диапазоне малых чисел (04:02) gp > \r 15unik.txt log = 1 (on) [logfile is "15unik_res.txt"] 3507 from number 4507 to number [0,18,30,60,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 703365638885910 - 904126689506040 2293760 formulae expected 710185785273343: [0, 10, 30, 60, 78, 88, 96, 106, 120, 130, 150, 184, 190, 210, 228] 710185785273343: [0, -8, 0, 0, 0, 4, -12, -8, 0, -14, 0, 16, -8, 0, 0] 710185785273343: [1, 0, 1, 1, 1, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1] valids=8 ncode=3625 822660735290773: [0, 16, 30, 60, 70, 84, 100, 114, 130, 136, 166, 168, 196, 210, 228] 822660735290773: [0, -2, 0, 0, -8, 0, -8, 0, 10, -8, 16, 0, -2, 0, 0] 822660735290773: [1, 0, 1, 1, 0, 1, 0, 1, 0, 0, 0, 1, 0, 1, 1] valids=8 ncode=3397 756712466267983: [0, 16, 46, 60, 78, 96, 106, 114, 136, 144, 150, 168, 198, 210, 228] 756712466267983: [0, -2, 16, 0, 0, 12, -2, 0, 16, 0, 0, 0, 0, 0, 0] 756712466267983: [1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1, 1, 1, 1, 1] valids=10 ncode=1631 772804111077223: [0, 18, 30, 60, 66, 84, 88, 114, 136, 148, 150, 154, 184, 190, 228] 772804111077223: [0, 0, 0, 0, -12, 0, -20, 0, 16, 4, 0, -14, -14, -20, 0] 772804111077223: [1, 1, 1, 1, 0, 1, 0, 1, 0, 0, 1, 0, 0, 0, 1] valids=8 ncode=7496 881135072746153: [0, 18, 58, 60, 64, 84, 108, 114, 120, 144, 150, 166, 180, 190, 228] 881135072746153: [0, 0, 28, 0, -14, 0, 0, 0, 0, 0, 0, -2, -18, -20, 0] 881135072746153: [1, 1, 0, 1, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 1] valids=10 ncode=5624 783563844401563: [0, 24, 30, 60, 78, 84, 108, 114, 120, 136, 144, 166, 190, 210, 228] 783563844401563: [0, 6, 0, 0, 0, 0, 0, 0, 0, -8, -6, -2, -8, 0, 0] 783563844401563: [1, 0, 1, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 1, 1] valids=10 ncode=4065 734055585201163: [0, 18, 30, 60, 78, 84, 96, 114, 136, 144, 150, 166, 198, 210, 228] 734055585201163: [0, 0, 0, 0, 0, 0, -12, 0, 16, 0, 0, -2, 0, 0, 0] 734055585201163: [1, 1, 1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 1, 1, 1] valids=12 ncode=8027 . . . . . . . В этом проходе проверка идёт в интервале search in 703365638885910 - 904126689506040 Счёт начинался с самого начала ряда простых чисел. Приближаемся к 1е15.
12) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14173) Posted 13 hours ago by Natalia Makarova Post: Г. Петухов писал в сообщении https://dxdy.ru/post1636845.html#p1636845 Так чем знание правильного названия поможет в программах если в них и так это уже реализовалось само собой? Или это лишь подводка к какому-то красивому эффективному результату из ТЧ? Не томите. Никакой "подводки" нет. Никаких "красивых эффективных результатов" не будет, не ждите. vicvolf уже довольно долго пыжится и топорщится, но ещё не сказал в теме абсолютно ничего. Ему надо самому почитать хотя бы тему "Симметричные кортежи из последовательных простых чисел". Дайте ему, наконец, ссылку на эту тему.
13) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14172) Posted 13 hours ago by Natalia Makarova Post: vicvolf писал в сообщении https://dxdy.ru/post1636843.html#p1636843 Очень хорошо, что не надо полного перебора для определения полноты системы вычетов для кортежа, но все равно для длинных кортежей вручную это невозможно. Это называется определением "проходимости" кортежа данной структуры, т.е. может ли быть кортежей такой структуры бесконечное количество. А нас только такие кортежи и интересуют. Вообще-то, это называется: определить, является ли данный паттерн допустимым или недопустимым (inadmissible patterns - согласно Википедии). И никто не делает это вручную, написать программу не так сложно. Да и она давно написана г. Петуховым и выложена на форуме dxdy.ru давным-давно. Как-то странно выглядят поучения человека, который недавно пришёл в тему и поучает людей, которые в теме уже много лет. vicvolf всерьёз думает, что в теме никто не знает базовых положений?
14) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14171) Posted 14 hours ago by Natalia Makarova Post: Интересная информация в сообщении по найденным мной уникальным элементам спектра приближений к ключевой 17-ке https://boinc.progger.info/odlk/forum_thread.php?id=277&postid=13992 Это по valids=12 valids=12 115 codes: [16325, 31335, 32333, 14799, 31465, 31545, 29983, 32310, 16227, 22259, 31181, 26525, 13305, 29621, 12276, 12259, 23027, 31218, 32534, 31697, 13935, 18414, 32285, 30441, 22427, 18407, 30179, 24532, 7639, 14297, 12245, 28529, 17915, 21437, 30437, 13263, 25582, 28632, 18359, 12797, 7543, 12735, 28402, 4078, 30696, 24123, 30606, 15819, 13803, 13805, 22454, 12203, 29657, 14111, 2043, 31459, 1983, 31899, 32624, 29166, 27510, 21423, 26556, 31799, 26301, 26455, 26598, 22475, 10079, 16338, 8178, 9725, 25071, 30123, 17403, 28581, 7149, 12261, 22478, 11959, 26571, 27102, 18239, 30627, 15069, 32166, 23529, 15767, 30323, 27591, 30109, 26541, 27633, 16051, 17343, 27603, 7667, 23523, 27118, 29673, 27951, 24395, 26943, 28117, 12094, 26063, 6138, 24530, 10747, 8165, 26423, 23015, 28390, 27069, 21479] Добавила сюда ещё один уникальный элемент - 16179. Может быть, и ещё были добавлены с момента выложенной статистики.
15) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14170) Posted 14 hours ago by Natalia Makarova Post: Новая порция Norm-чисел для ключевой 17-ки дала отличное приближение с valids=12 в заоблачных высотах 10188725126826790625150743: [0, 18, 24, 36, 66, 84, 90, 114, 126, 136, 150, 156, 186, 198, 216, 234, 240] 10188725126826790625150743: [0, 12, 0, 0, 0, 0, 0, 0, 6, 10, 0, 0, 12, -6, 0, 0, 0] valids=12 code=16179 Да ещё и элемент спектра уникальный! 16179 10188725126826790625150743 Добавила элемент в спектр. Напомню: на данный момент спектр приближений к ключевой 17-ке содержит 27735 уникальных элементов. Надо всё-таки его выложить на Яндекс.Диск, чтобы не потерялся. Выложила https://disk.yandex.ru/d/kntzjUzYCsAcpQ 563 КБ. Господа! Кто занимается темой, скопируйте спектр, пригодится. gris, а вам просто необходимо скопировать и снова проверить спектр на ошибки, но только выдать правильные предупреждения, чтобы можно было в них разобраться :) Если уж не мне, то, по крайней мере, вам.
16) Message boards : Cafe : Игра Кликер (Message 14169) Posted 19 hours ago by Natalia Makarova Post: На новой черепашке :) не рекорд, но всё равно хорошо сыграли Сделала последнюю попытку, вылетела из игры, не уследила, поэтому картинка плохая.
17) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14168) Posted 22 hours ago by Natalia Makarova Post: Вот ещё с тремя "дырками" приближение к центральной 15-ке в диапазоне малых чисел 215505208558319: [0, 18, 30, 60, 78, 84, 102, 110, 120, 144, 150, 158, 198, 210, 228] 215505208558319: [0, 0, 0, 0, 0, 0, -6, -4, 0, 0, 0, -10, 0, 0, 0] 215505208558319: [1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 1, 1] valids=12 ncode=7995 Код в верхней части спектра. А с двумя "дырками" нету :(
18) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14167) Posted 22 hours ago by Natalia Makarova Post: Да, чуть не забыла, это на Ахиллесе-3 обрабатывались 5000 периодов 31# . . . . . . . . . . 9918096563639529659: [0, 20, 30, 38, 50, 84, 98, 114, 120, 140, 150, 168, 174, 198, 228] 9918096563639529659: [0, 2, 0, -22, -28, 0, -10, 0, 0, -4, 0, 0, -24, -12, 0] 9918096563639529659: [1, 0, 1, 0, 0, 1, 0, 1, 1, 0, 1, 1, 0, 0, 1] valids=8 ncode=2412 9917909955707278919: [0, 18, 50, 60, 84, 92, 98, 114, 120, 140, 164, 170, 198, 210, 228] 9917909955707278919: [0, 0, 20, 0, 6, 8, -10, 0, 0, -4, 14, 2, 0, 0, 0] 9917909955707278919: [1, 1, 0, 1, 0, 0, 0, 1, 1, 0, 0, 0, 1, 1, 1] valids=8 ncode=5219 9917875054689597389: [0, 20, 50, 60, 62, 84, 108, 114, 128, 144, 162, 164, 168, 210, 228] 9917875054689597389: [0, 2, 20, 0, -16, 0, 0, 0, 8, 0, 12, -4, -30, 0, 0] 9917875054689597389: [1, 0, 0, 1, 0, 1, 1, 1, 0, 1, 0, 0, 0, 1, 1] valids=8 ncode=1489 9918693573330297149: [0, 18, 42, 60, 62, 72, 78, 114, 120, 144, 164, 168, 210, 224, 228] 9918693573330297149: [0, 0, 12, 0, -16, -12, -30, 0, 0, 0, 14, 0, 12, 14, 0] 9918693573330297149: [1, 1, 0, 1, 0, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1] valids=8 ncode=5236 time = 24h, 12min, 16,359 ms. Сутки. На черепашке 1000 периодов обрабатываются 2,5 часа. Ну, в следующем проходе на Ахиллесе-3 задала 2000 периодов. Мне надо побыстрее получать новые элементы, чтобы формировать новый массив пропущенных элементов (и для черепашки тоже).
19) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14166) Posted 22 hours ago by Natalia Makarova Post: Вот посмотрите-ка, на Ахиллесе-3 программа работает в диапазоне больших чисел (с новым массивом пропущенных элементов) ? \r 15unik.txt logfile = "15unik_res.txt" 49428919 from number 49430918 to В number [0,18,30,60,78,84,108,114,120,144,150,168,198,210,228] patterns length 15 prove by 31#: [2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31] 200560490130 period search in 9913488221236069470 - 9913889342216329470 2293760 formulae expected 9913488959103343993: [0, 58, 60, 66, 78, 84, 108, 126, 130, 136, 150, 168, 198, 210, 228] 9913488959103343993: [0, 40, 30, 6, 0, 0, 0, 12, 10, -8, 0, 0, 0, 0, 0] 9913488959103343993: [1, 0, 0, 0, 1, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1] valids=9 ncode=911 Выдала одно решение и... тишина. Да, тут будет такой темп, и с таким темпом спектр будет заполняться десять лет. Ну, надежда на диапазон малых чисел, там пока идут новые элементы.
20) Message boards : Cafe : Проект gris по кортежу 19-252 (Message 14165) Posted 23 hours ago by Natalia Makarova Post: Новая порция Norm-чисел для 19-ки с минимальным диаметром дала следующие приближения с valids=10 10042376698946948800912681: [0, 10, 12, 30, 36, 42, 76, 82, 96, 126, 132, 136, 162, 166, 210, 220, 240, 246, 252] 10042376698946948800912681: [0, 4, 0, 0, -6, -30, -14, -14, -24, 0, 0, -20, 0, -14, 0, -2, 0, 0, 0] valids=10 code=49579 10042376697647632705160461: [0, 6, 12, 42, 48, 52, 90, 106, 108, 126, 136, 156, 160, 180, 208, 222, 232, 246, 252] 10042376697647632705160461: [0, 0, 0, 12, 6, -20, 0, 10, -12, 0, 4, 0, -2, 0, -2, 0, -8, 0, 0] valids=10 code=100693 Интересно: в первом приближении содержится приближение к центральной 15-ке, а во втором приближении содержится приближение к ключевой 17-ке. Приближение к центральной 15-ке 10042376698946948800912693: 12, 30, 36, 42, 76, 82, 96, 126, 132, 136, 162, 166, 210, 220, 240 приближение к ключевой 17-ке 10042376697647632705160467: 6, 12, 42, 48, 52, 90, 106, 108, 126, 136, 156, 160, 180, 208, 222, 232, 246 (паттерны не нормализованы) Отлично! Идея напрашивается: искать программой поиска Norm-чисел для 19 с минимальным диаметром также Norm-числа для ключевой 17-ки и для центральной 15-ки. Вдруг найдётся что-нибудь интересненькое. PS. Вот утилитой проверила приближения к 15-ке и к 17-ке 10042376698946948800912693: [0, 18, 24, 30, 64, 70, 84, 114, 120, 124, 150, 154, 198, 208, 228] 10042376698946948800912693: [0, 0, -6, -30, -14, -14, -24, 0, 0, -20, 0, -14, 0, -2, 0] valids=7 code=4202 10042376697647632705160467: [0, 6, 36, 42, 46, 84, 100, 102, 120, 130, 150, 154, 174, 202, 216, 226, 240] 10042376697647632705160467: [0, 0, 12, 6, -20, 0, 10, -12, 0, 4, 0, -2, 0, -2, 0, -8, 0] valids=8 code=17578 Коды не уникальные.

Next 20